Άλγεβρα / Algebra
Συνέχειες
Submitted by ltme on Wed, 07/17/2013 - 16:24Αναγνωρίζω, αναλύω και αντιγράφω μοτίβα
Submitted by trikka on Mon, 06/17/2013 - 17:34Τρίκκα Γεωργία
Περίληψη:
Καθώς η ομάδα παιδιών και εγώ βρισκόμαστε γύρω από τον υπολογιστή και παρατηρούμε τα δεδομένα της οθόνης, εφιστώ την προσοχή των μαθητών σε ένα συγκεκριμένο σχήμα που προβάλλεται. Τα παιδιά αναλύουν το σχήμα αυτό σε γεωμετρικά σχήματα και σε χρώματα, μετράνε και αθροίζουν τα επιμέρους αυτά σχήματα, και τέλος «διαβάζουν» τον τρόπο με τον οποίο αυτά είναι διαταγμένα κάνοντας έτσι την αναγνώριση του μοτίβου του αρχικού σχήματος. Με γνώμονα αυτή την ανάλυση τα παιδιά δημιουργούν ένα αντίγραφο του αρχικού σχήματος κοντά σε αυτό επαληθεύοντας τα δεδομένα που αναγνώρισαν προηγουμένως.
Λογισμικά:
Τι μαθηματικά κάνω;:
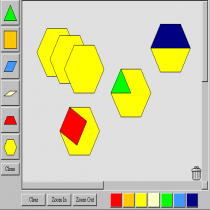
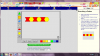
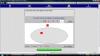
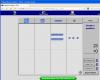
Από τον Άξονα Μαθηματικών Εννοιών της Άλγεβρας επέλεξα τοVirtual Manipulative “Pattern Blocks”. Το συγκεκριμένο Virtual Manipulative θεωρώ πως είναι ιδανικό για να εξασκηθούν τα παιδιά του νηπιαγωγείου στην αναγνώριση γεωμετρικών σχημάτων και χρωμάτων, στο μέτρημα, στην πρόσθεση, στην αντίληψη και αναπαραγωγή δεδομένων μοτίβων.
Τι δράση μπορώ να σχεδιάσω για τα παιδιά;:
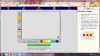
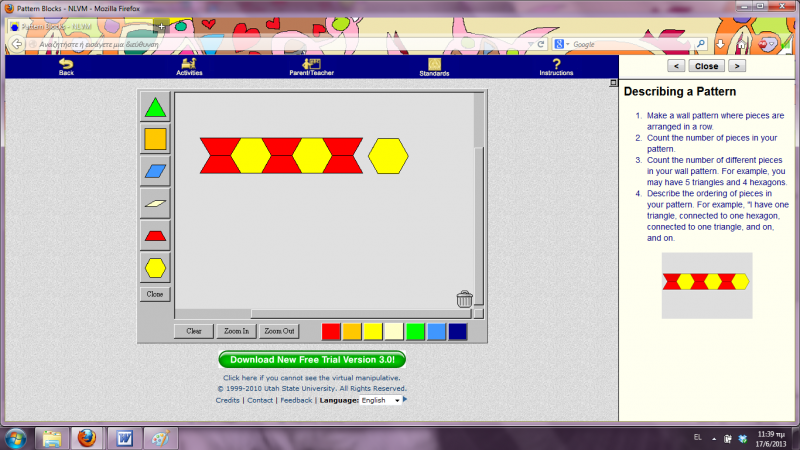
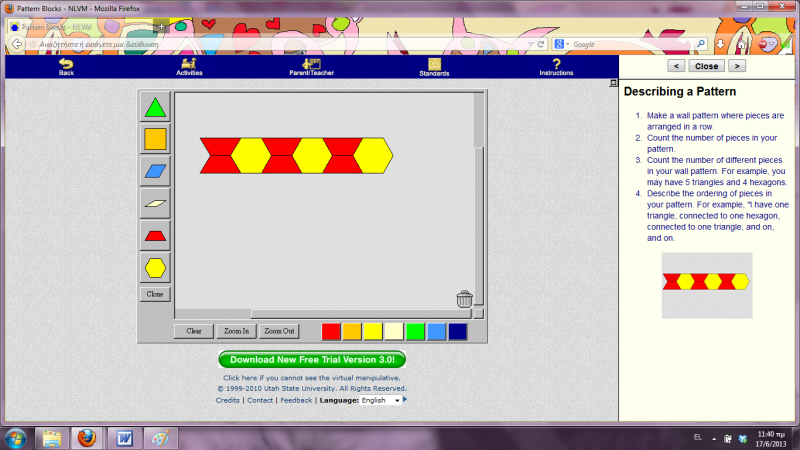
Αρχικά, αφού μαζέψω την ομάδα παιδιών γύρω από τον υπολογιστή, ανοίγοντας το VM αυτό, τα ρωτάω τι παρατηρούν σε αυτό που προβάλλεται στην οθόνη του υπολογιστή. Αφού, ίσως και με τη δική μου βοήθεια ή παρότρυνση, αναγνωρίσουν το μεγάλο ορθογώνιο πλαίσιο στο κέντρο, τα σχήματα που περιέχει μέσα και τα χρώματά τους, οδηγώ την προσοχή τους στην χρωματιστή εικόνα δεξιά της οθόνης. Πρώτα ζητώ να αναγνωρίσουν τα χρώματα που βλέπουν στο σχήμα της εικόνας αυτής. Έπειτα τους λέω να παρατηρήσουν το προβαλλόμενο σχήμα (Α). Μήπως αναγνωρίζετε μέσα σε αυτό γνωστά σας γεωμετρικά σχήματα; Αυτά τα σχήματα έχουν ίδιο ή διαφορετικό χρώμα μεταξύ τους; Ποια έχουν κόκκινο και ποια κίτρινο χρώμα; Αφού γίνει η αναγνώριση των σχημάτων και των χρωμάτων τους, τα παιδιά μπορούν να μετρήσουν πλέον πόσα είναι τα τραπέζια της εικόνας και πόσα τα εξάγωνα. Μετά τους ρωτώ πόσα είναι όλα τα σχήματα του σχεδίου Α. Για να αντιληφθούν καλύτερα το εικονιζόμενο μοτίβο παροτρύνω να περιγράψουν το σχήμα Α που βλέπουν χρησιμοποιώντας τα μικρότερα γεωμετρικά σχήματα (τραπέζιο, εξάγωνο) και τη σειρά με την οποία αυτά παρουσιάζονται (από αριστερά προς τα δεξιά > δύο παραλληλόγραμμα το ένα πάνω στο άλλο, ένα εξάγωνο, δύο παραλληλόγραμμα το ένα πάνω στο άλλο, ένα εξάγωνο, δύο παραλληλόγραμμα το ένα πάνω στο άλλο, ένα εξάγωνο).
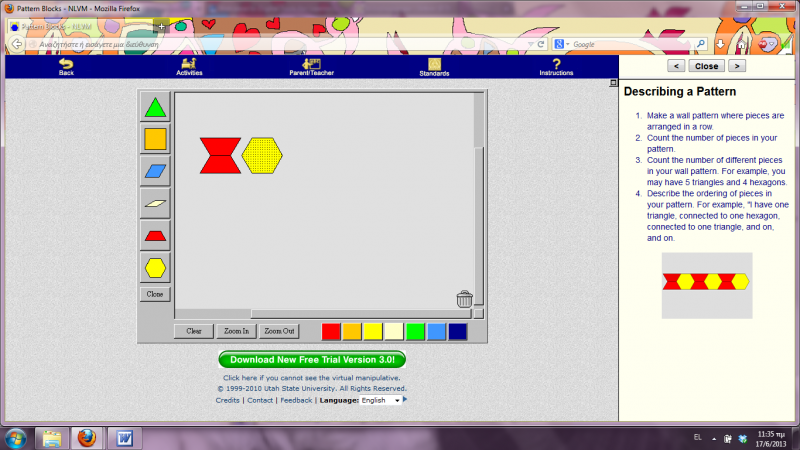
Αφού λοιπόν αναλύσαμε αρκετά το σχήμα Α δεξιά στην οθόνη, γυρνάμε στο κέντρο της και ζητώ από μεμονωμένα παιδιά να μου δημιουργήσουν με τα εργαλεία που γνωρίσαμε νωρίτερα το ίδιο μοτίβο Α θυμίζοντάς τους, όπου βρίσκουν δυσκολία, τα συμπεράσματα που αναφέραμε πριν για το μοτίβο αυτό (σχετικά με τα σχήματα που το απαρτίζουν, τα χρώματά τους, τη διάταξη και το πλήθος τους). Μετά την ορθή ολοκλήρωση της αντιγραφής του μοτίβου Α, μπορούμε να πατήσουμε το clear για να καθαρίσει η οθόνη και να έρθει ένα άλλο παιδί να επαναλάβει την άσκηση αυτή.
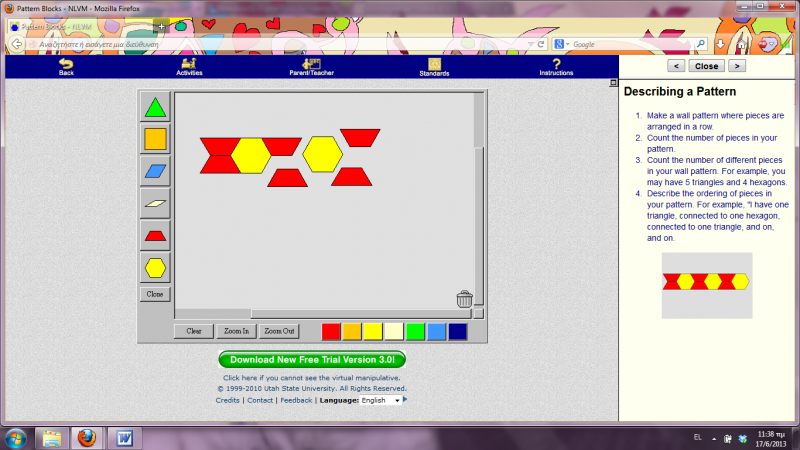
Απώτερος σκοπός είναι τα παιδιά να κατανοήσουν ότι ένα σχήμα που αρχικά μπορεί να φαίνεται άγνωστο, μπορεί να εμπεριέχει μέσα του γνωστά γεωμετρικά σχήματα τα οποία δημιουργούν ένα μοτίβο. Αν αυτό το μοτίβο αναγνωριστεί και αναλυθεί σωστά, τότε μπορούμε να δημιουργήσουμε μόνοι μας “κλώνους” του ίδιου σχήματος.
Τι σχέση έχει με το Αναλυτικό Πρόγραμμα;:
Με τη δράση αυτή, σύμφωνα με το Νέο Αναλυτικό Πρόγραμμα και την ενότητα Παιδί και Μαθηματικά (Πρόγραμμα Σχεδιασμού και Ανάπτυξης Δραστηριοτήτων Μαθηματικών) τα παιδιά εμπλέκονται σε καταστάσεις προβληματισμού και επεξεργάζονται σχήματα, χρώματα, σχέσεις, και αριθμούς. Προβληματίζονται πάνω στο μοτίβο Α , ερευνούν ποικίλες καταστάσεις, στηρίζονται σε προηγούμενες γνώσεις και εμπειρίες, κάνουν απλές υποθέσεις και καταλήγουν σε σχετικά συμπεράσματα. Τους δίνεται η ευκαιρία να παρατηρήσουν, να περιγράψουν, να συγκρίνουν και να ταξινομήσουν με βάση ορισμένα γνωρίσματα που είναι κοινά στα αντικείμενα της δράσης μας. Αναγνωρίζουν και ονομάζουν γεωμετρικά σχήματα, απαριθμούν αντικείμενα, βάζουν τα σχήματα στη σειρά και έτσι εξοικειώνονται με τα τακτικά αριθμητικά. Ενθαρρύνονται να αντιλαμβάνονται και να αναπαράγουν δεδομένα μοτίβα. Τέλος, τα παιδιά μαθαίνουν πώς να αξιοποιούν την τεχνολογία και εξοικειώνονται με αυτή.
Εικόνες σχετικές με τη δράση:
Πρόσθεση θετικών και αρνητικών αριθμών
Submitted by siaka on Sun, 06/16/2013 - 21:34Σιάκα Κωνσταντίνα
Περίληψη:
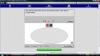
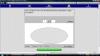
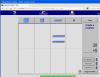
Έχω επιλέξει το λογισμικό Color Chips-Addition. Με το πρόγραμμα αυτό τα παιδιά μαθαίνουν την έννοια της πρόσθεσης καθώς αποκτούν και μια επαφή με τους θετικούς και τους αρνητικούς αριθμούς.Είναι ένα πολύ απλό λογισμικό το οποίο μας καθοδηγεί πλήρως και έτσι η πρόσθεση γίνεται παιχνίδι στα χέρια των παιδιών.
Λογισμικά:
Τι μαθηματικά κάνω;:
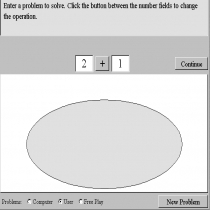
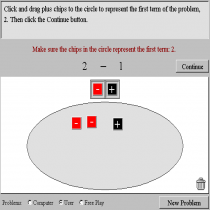
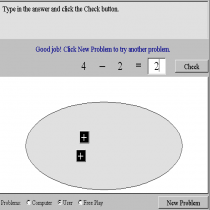
Χρησιμοποιώ την έννοια της προσθεσης των ακεραιων με θετικό και αρνητικό προσημο. Γίνετια ευκολο για τα παιδια να το κατανοησουν, καθως με χρωματα οπως κοκκινο και μαυρο ξεχωριζουν θετικούς και αρνητικούς αριθμούς.
Τι δράση μπορώ να σχεδιάσω για τα παιδιά;:
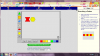
Με το λογισμικο που επελεξα μπορεις να κανεις μονο προσθεσεις, καθως στα μαθηματικα η μια απο τις δυο βασικες πραξεις ειναι η προσθεση. Μπορω ευκολα να βρισκω αποτελεσμα μεσα απο ενα διασκεδαστικο και ευκολο τροπο τοποθετώντας τα αντιθετα προσημα το ενα επανω στο αλλο και εκεινα εξαφανιζονται. Ετσι οταν εχω μονο ενα χρωμα στο κουτι κατω απο τη γραμμη της πραξης ειναι ετοιμο και το αποτελεσμα μου. Το σημειωνω στο κουτακι διπλα απο την πραξη και παταω check. Επισης εκτος απο τα προβληματα που ειναι ηδη προγραμματισμενα μπορω να βαλω και οποιουσδηποτε αριθμους θελω εγω.
Στα παιδια μπορω να πω πως οσα κουτακια ειναι μαυρα αντιστοιχουν σε τσιχλες που παιρνω και τα κοκκινα σε τσιχλες που δινω. Αρα στο τελος της ασκησης τους,που θα ειναι σαν παιχνιδι, θα ξερουν και ποσες τσιχλες παιρνουν ή ποσες τσιχλες πρεπει να δωσουν.
Τι σχέση έχει με το Αναλυτικό Πρόγραμμα;:
Με βαση το προγραμμα που επελεξα η καταλληλοτερη ηλικια για να χρησιμοποιησει το λογισμικο αυτο ειναι τα παιδια 5-6 ετων. Πρωτος μου σκοπος ειναι τα παιδια να μπορουν να ξεχωρισουν τους αριθμους,δηλαδη τους θετικους απο τους αρνητικους και να βαλουν τα καταλληλα κουτακια στο γκρι οβαλ πεδιο. Τα παροτρυνω ροκαλω κατα καποιο τροπο να καταλαβουν ποιο απο τα δυο θα υπερισχυσει και να μου πουν το προσημο του αποτελεσματος χωρις να ειναι δεσμευτικο να το υπολογισουν πριν τη χρηση του προγραμματος. Ζηταω επειτα το καθε παιδι ξεχωριστα με τη σειρα του να ερχεται να χρησιμοποιει αυτο το εργαλειο με τη βοηθεια μου ή με τη βοηθεια της συναδελφου νηπιαγωγου. Θελω ολα τα παιδια να προσεχουν το προσημο του καθε αριθμου και να τοποθετουν τα κοκκινα και τα μαυρα κουτακια με προσοχη και χωρις να βιαζονται.
Εικόνες σχετικές με τη δράση:
Χρωματιστές σειρές
Submitted by tsanteki on Sat, 06/15/2013 - 19:39Τσαντεκίδου Ελένη
Περίληψη:
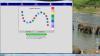
Η εν λόγω εργασία έχει θέμα την εκμάθηση των μαθηματικών μέσω virtual manipulatives και συγκεκριμένα τη χρήση color patterns. Τα παιδιά με τη βοήθεια των χρωματιστών σημείων, τα οποία είναι πιο ελκυστικά για τους μικρούς μαθητές δεδομένου πως τα παιδιά δεν βλέπουν τα color patterns ως μια μαθηματική εργασία αλλά ως παιχνίδι που τα βοηθάει να αναπτύξουν τη μαθηματική τους σκέψη μέσω της ψυχαγωγίας.
Λογισμικά:
Τι μαθηματικά κάνω;:
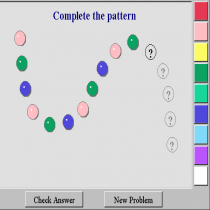
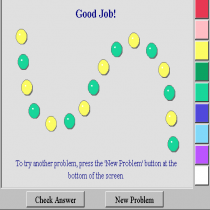
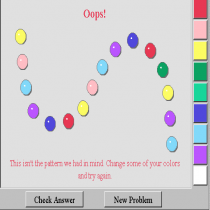
Το color patterns των virtual manipulativesβοηθάει τα παιδιά στην κατάκτηση του μαθηματικού αλφάβητου, της ικανότητας δηλαδή του ατόμου να κωδικοποιεί, να αφομοιώνει και να παρουσιάζει τα μαθηματικά σε μια ποικιλία χρωματιστών πλαισίων. Χρησιμοποιεί τη μαθηματική σκέψη και μαθηματικές έννοιες, διαδικασίες, δεδομένα και εργαλεία για να περιγράψει , να εξηγήσει και να προβλέψει φαινόμενα. Συγκεκριμένα το color pattern θεωρώ ότι βοηθάει τα παιδιά να αναγνωρίσουν το ρόλο που παίζουν τα μαθηματικά στη ζωή μας, στις καθημερινές τους ασχολίες ακόμα και στο παιχνίδι τους. Τα virtual manipulatives κατά την άποψή μου είναι απαραίτητα εργαλεία, εύχρηστα, δωρεάν διαθέσιμα στο διαδίκτυο για την διδασκαλία των μαθηματικών και συγκεκριμένα της άλγεβρας.
Τι δράση μπορώ να σχεδιάσω για τα παιδιά;:
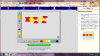
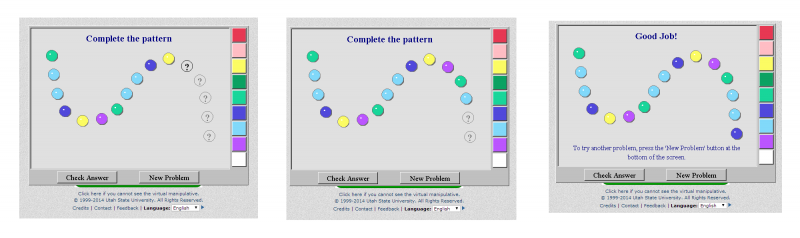
Κατα τη χρήση του virtual manipulatives και συγκρεκριμένα του color patterns τα παιδιά καλούνται να συμπληρώσουν το χρώμα του σχεδίου που λείπει σύμφωνα με το πρότυπο που ήδη υπάρχει ξεκινώντας από την πάνω αριστερά μεριά του χώρου εργασίας. Τα χρώματιστά σχέδια επαναλαμβάνονται και το παιδί καλείται να βρεί τη σειρά των χρωμάτων που του φαίνεται περισσότερο αποτελεσματική. Ο ενήλικας θα πρέπει να σιγουρευτεί ότι τα παιδιά κατάλαβαν τα ΄χρωματιστά πρότυπα, τα οποία επαναλαμβάνονται κάτι που θα το βοηθήσει στη συνέχεια να συμπληρώσει τα κενά σχέδια και να ενθαρύνει τους μαθητές να χρησιμοποιήσουν τα δικά τους λόγια για να περιγράψουν τις συνήθεις που παρατηρούν. Μόλις ένα πρότυπο παρατηρείται οι μαθητές θα πρέπει να επεκτείνουν το μοτίβο κάνοντας κλικ σε ένα κουμπί με ένα ερωτηματικό και κάνοντας κλίκ στο αντίστοιχο χρώμα. Eν συνεχεία μπορούν να διορθώσουν τυχόν λάθη ή να ελέγξουν μετά το τέλος της διαδικασίας την ορότητα των απαντήσεών τους κάνοντας κλικ στην επιλογή "έλεγχος". Κατα τη διάρκεια αυτής της διαδικασίας ο ενήλικας θα πρέπει να ενθαρύνει τα παιδιά να χρησιμοποιουν τα δικά τους λόγια για να περιγράψουν τις συνήθειες που παρατηρούν. Μετά από αυτήν την εργασία χειραγώγησης μπορεί να φανεί διασκεδαστικό στα παιδιά να πάνε στο block pattern για να δημιουργήσουν το δικό τους πρότυπο και να έχουν έναν άλλο μαθητή να συνεχίσει αυτό το μοτίβο που δημιούργησαν.
Τι σχέση έχει με το Αναλυτικό Πρόγραμμα;:
Σύμφωνα με το αναλυτικό πρόγραμμα του Υπουργείου Παιδείας στη χώρα μας, οι μαθητές μέσω της διδασκαλίας των μαθηματικών εκτιμούν την αξία των μαθηματικών σε όλους τους τομείς της ανθρώπινης δραστηριότητας, καλλιεργούν την αυτοπεποίθησή τους χρησιμοποιόνταςτα μαθηματικά ως δημιουργική απασχόληση. Επιπλέον βοηθούν τα παιδιά ώστε να αναπτύσσουν στάσεις, γνώσεις και δεξιότητες, να κατανοούν έννοιες που θα τους βοηθήσουν να χρησιμοποιούν τα μαθηματικά στην ερμηνεία προβλημάτων από διάφορα γνωστικά αντικείμενα. Επιπλέον αποκτούν τις απαραίτητες γνώσεις που απαιτούνται στη σύγχρονη κοινωνία της πληροφορίας ενώ ταυτόχρονα βοηθούν να καλλιεργήσουν γνώσεις και δεξιότητες, για να συνεχίσουν τις σπουδές τους σε αντικείμενα στα οποία η χρήση των μαθηματικών είναι απαραίτητη. Προς την ίδια κατεύθυνση στοχεύει και η δράση που σχεδιάσαμε.
Εικόνες σχετικές με τη δράση:
Μια βόλτα με το λεωφορείο
Submitted by panela on Sat, 06/15/2013 - 16:30Πανέλα Αποστολία
Περίληψη:
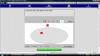
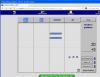
Η επιλογή του virtual manipulative base block adittion αφορά αριθμητικές πράξεις και ανήκει στην κατηγορία της άλγεβρας. Στόχος είναι τα νήπια να προσεγγίσουν την έννοια των αριθμών και να εξοικειωθούν με τα σύμβολά τους . Ακόμη, να προσεγγίσουν βασικούς λογικό-μαθηματικούς συλλογισμούς και ιδιαίτερα αυτούς που σχετίζονται με την έννοια των δυο αριθμητικών πράξεων(πρόσθεση και αφαίρεση).Πιο συγκεκριμένα, ειναι μία δραστηριότητα επίλυσης προβλήματος η οποία δημιουργεί κίνητρα κι ενθαρρύνει τα νήπια ώστε να κάνουν επιλογές και να παίρνουν αποφάσεις. Τίτλος δράσης "μία βόλτα με το λεωφορείο". Η σχέση που έχει με το αναλυτικό πρόγραμμα βρίσκεται στην περιοχή της πρόσθεσης-αφαίρεσης.
Λογισμικά:
Τι μαθηματικά κάνω;:
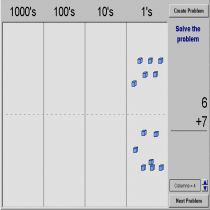
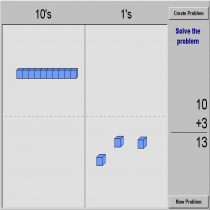
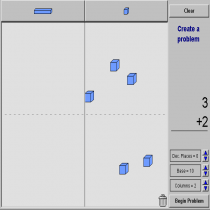
Το virtual manipulative που επιλέχθηκε , ανήκει στον μαθηματικό κλάδο της άλγεβρας και συγκεκριμένα ασχολείται με τις μαθηματικές πράξεις της αφαίρεσης και της πρόσθεσης . Τα παιδιά από πολύ νωρίς εκφράζουν λογικό μαθηματικές σκέψεις έτσι είναι προτιμότερο και ευκολότερο να μεταδοθούν αυτές οι γνώσεις μέσω εκπαιδευτικών λογισμικών καθώς η μάθηση γίνεται πιο κατανοητή και ενδιαφέρουσα. Τα αποτελέσματα των επιλογών που κάνουν τα νήπια είναι αποτέλεσμα κριτικής σκέψης ιδιαίτερα όταν αναφέροντα σε πραγματικές καταστάσεις από τον βιοματικό χώρο των παιδιών όπου και αναφέρεται η παρούσα δραστηριότητα. Επιπλέον , τα παιδιά μπορούν να εξασκιθούν στην πράξη της πρόσθεσης μέσω ενός περιβάλλοντος που κινεί το ενδιαφέρον τους και μπορεί να κάνει κατανοητές ορισμένες έννοιες όπως μονάδες δεκάδες συν πλιν.
Τι δράση μπορώ να σχεδιάσω για τα παιδιά;:
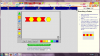
Αρχικά , τα παιδιά καλούνται να επεξεργαστούν το περιβάλλον του vir tual manipulative base block adittion μετακινώντας με το ποντίκι τις μονάδες , τις δεκάδες και τις χιλιάδες . Η εικονοποίηση αυτών σε τρισδιάσταση μορφή μπορούν να βοηθήσουν τα παιδιά να κατανοήσουν καλύτερα τους όρους έχοντας την δυνατότητα να μετρήσουν ένα ένα τα κουτάκια και να αντιληφθούν πως μιλάμε για δέκα κουτάκια συνεπώς, για μια δεκάδα . Στη συνέχεια της διδακτικής πράξης, προβάλλω ένα πρόβλημα προς επίλυση στα παιδιά. Το πρόβλημα είναι το εξής : Ξεκινάει ένα λεωφορείο από την αφετηρία του , στην πρώτη στάση ανεβαίνουν 10 άτομα , στην επόμενη στάση ανεβαίνουν άλλα δέκα και μετά από αρκετές στάσεις άλλα 3 άτομα . Πόσα άτομα είναι αυτή τη στιγμή στο λεωφορείο ; Τα παιδιά καλούνται να τοποθετήσουν στην οθόνη δυο δεκάδες είτε , είκοσι μονάδες , και στη συνέχεια να προσθέσουν άλλα 3 για να μπορέσουν να βρούν το αποτέλεσμα. Αν αυτό το κομμάτι φανεί δύσκολο στα παιδιά , με τη βοήθεια μας μπορούν να τοποθετηθούν οι δεκάδες καλώντας τα παιδιά να μετρήσουν και στην πορεία να προστεθούν από τα ίδια τα παιδιά άλλα τρία κυβάκια σύμφωνα με τον αριθμό των επιβατών που θέλουν να ανέβουν στο λεωφορείο. Κατά τη διάρκεια επεξεργασίας της δραστηριότητας η νηπιαγωγός οφείλει να βοηθάει την εξέλιξη της, με διάφορες προσδιοριστικές ερωτήσεις , τύπου: Πόσα κουτάκια βλέπετε στην οθόνη ;μπορείτε να τα μετρήσετε; αναγνωρίζετε το σύμβολο δεξιά της οθόνης; τι πράξη πιστεύετε ότι πρέπει να κάνουμε; πόσα άτομα ακόμα θέλουν να ανέβουν στο λεωφορείο; μπορείτε να μου δείξετε με το ποντίκι και τα κυβάκια ; πόσα άτομα είναι τώρα στο λεωφορείο ; είναι περισσότερα ή λιγότερα από πριν ; Tα παιδιά ιδανικά θα πρέπει να πουν πως στο λεωφορείο υπάρχουν 23 άτομα.
Τι σχέση έχει με το Αναλυτικό Πρόγραμμα;:
Το virtual manipulative με το νέο αναλυτικό πρόγραμμα συνδέεται στην περιοχή της πρόσθεσης και της αφαίρεσης . Συγκεκριμένα , τα παιδιά μπαίνουν στη διαδικασία να προσεγγίσουν τις πράξεις , να συγκρίνουν και να λύσουν απλά προβλήματα πρόσθεσης και αφαίρεσης και να οδηγηθούν στα συμπεράσματα τους. Επιπλέον , ενθαρρύνονται να καταμετρούν ποσότητες και αξιοποιούν το ψηφιακό περιβάλλον για δραστηριότητες μαθηματικών και αρίθμησης.
Εικόνες σχετικές με τη δράση:
Ο πολλαπλασιασμός ως επαναλαμβανόμενη πρόσθεση
Submitted by valiappii on Fri, 06/14/2013 - 18:51Η έννοια του μοτίβου
Submitted by mariapsycha on Sun, 06/09/2013 - 20:15Ψύχα Μαρία
Περίληψη:
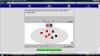
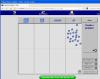
Ο άξονας που επέλεξα ήταν “αριθμοί και πράξεις” (Numbers and operations) για την ηλικία 3- 5 ετών και Virtual Manipulative ήταν το Color and Patterns το οποίο σχετίζεται με την ακολουθία μοτίβων. Οι λόγοι που το επέλεξα ήταν γιατί καταρχάς είναι ένα εύκολο και διασκεδαστικό παιχνίδι και ίσως το μοναδικό που συνοδεύται με ήχους κατά τη διάρκεια του παιχνιδιού, στο τέλος για επιβράβευση ή όταν κάτι δεν έχουμε κάνει πολύ σωστά. Τα παιδιά μπορούν να χρησιμοποιήσουν τις δικές τους γνώσεις και να πειραματιστούν με στόχο να ανακαλύψουν την έννοια της συνεχής ακολουθίας, της κανονικότητας. Θεωρώ ότι υποστηρίζει αρκετά καλά το πλαίσιο για την εξάσκηση της διερεύνησης, αναγνώρισης, συμπλήρωσης κανονικοτήτων. Επιπλέον μπορεί να χρησιμοποιηθεί για την έννοια της άμεσης εκτίμησης ποσότητας, της καταμέτρησης, ακόμα και των πράξεων με κατάλληλη βοήθεια από τον γονιό ή τον εκπαιδευτικό.
Λογισμικά:
Τι μαθηματικά κάνω;:
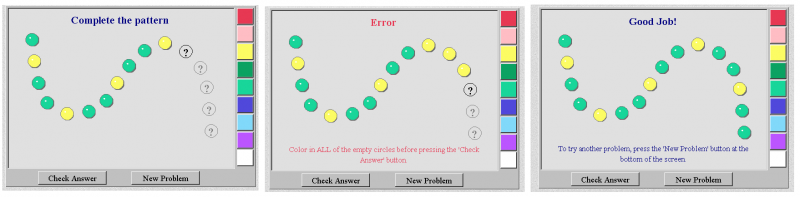
Ο μαθηματικός άξονας που εστιάζει το vm είναι Αριθμοί και Πράξεις, όμως αν παρατηρήσουμε καλά η NVLM εντάσει το ίδιο παιχνίδι και στον άξονα της Άλγεβρας. Αυτό είναι κάτι το αναμενόμενο αφού η έννοια της κανονικότητας που εξασκείται με τη χρήση του συγκεκριμένου virtual manipulative ανήκει στην θεματική ενότητα της Άλγεβρας. Τα προσδωκόμενα μαθησιακά αποτελέσματα είναι τα εξής: η αναγνώριση ύπαρξης μιας κανονικότητας, η συμπλήρωση και η επανάληψη μιας κανονικότητας, η περιγραφή και η εξήγηση επαναλαμβανόμενων κανονικοτήτων. Οι δραστηριότητες που προτείνονται είναι α) οι μαθητές να συγκρίνουν αντικείμενα με κριτήριο την ύπαρξη μοτίβου ή άλλης κανονικότητας β) να συμπληρώνουν κατασκευές με την επανάληψη μοτίβου γ) να κατασκευάζουν δικά τους αντικείμενα (π.χ. κομπολόγια, συνθέσεις σχημάτων) και να παρουσιάζουν τον κανόνα του δικού τους μοτίβου.
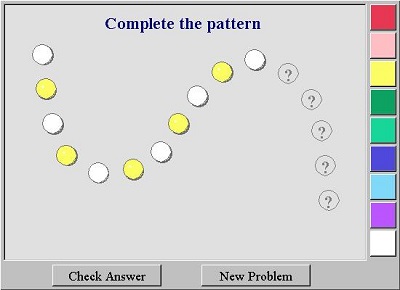
Η χρήση τεχνολογικού περιβάλλοντος με μοτίβα του πανεπιστημίου Utah των ΗΠΑ είναι μια άριστη επιλογή για την πραγματοποιήση παρόμοιων δραστηριοτήτων, όπως προτείνεται και απο το Αναλυτικό Πρόγραμμα. Επιπλέον μπορούν να αναπτυχθούν η έννοια της άμεσης εκτίμησης ποσότητας, η καταμέτρηση αντικειμένων σε εικόνες και συμβολικές παραστάσεις, για παράδειγμα έχω 2 κόκκινες φουσκίτσες και μία πράσινη κλπ.. Η αρίθμηση, ( για να μετρήσουμε πόσες μπαλίτσες είναι όλες...), ακόμα και οι πράξεις ( μία κόκκινη και δυο πράσινες πόσσες μας κάνουν); Κατά τη διάρκεια της δράσης αφήνουμε τα παιδιά ελεύθερα να χρησιμοποιήσουν τις δικές τους λέξεις για να μας περιγράψουν το μοτίβο (π.χ. μπαλίτσες ή κυκλάκια ή φουσκίτσες ή κομπολόι κλπ). Με το παιχνίδι μπορούν ακόμα να κάνουν νοερές εικόνες και έτσι να αναπτύξουν την φαντασία τους.
Τι δράση μπορώ να σχεδιάσω για τα παιδιά;:
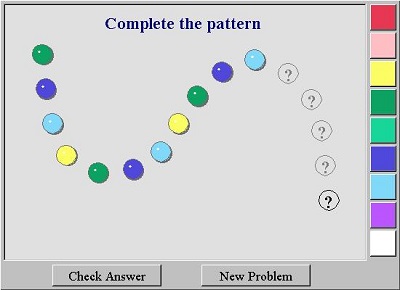
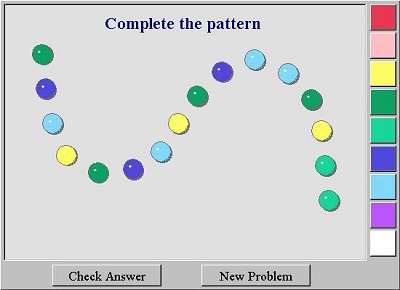
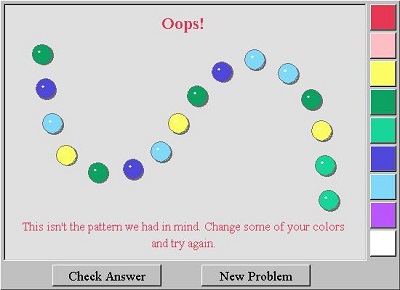
Θέλουμε να σιγουρευτούμε ότι οι μαθητές ξέρουν ότι τα μοτίβα είναι πράγματα επαναλαμβανόμενα και ότι είμαστε ικανοί να αναγνωρίσουμε και να περιγράψουμε μοτίβα , γιατί η περιγραφή και η πρόβλεψη γίνεται έτσι ευκολότερη. Οι μαθητές θα ωφεληθούν περιγράφοντας την ακολουθία των έγχρωμων κουμπιών ξεκινώντας από την πάνω αριστερή γωνία της επιφάνειας εργασίας. Καθώς δημιουργείται η ακολουθία, το κάθε κουμπάκι συνοδεύεται και απο έναν ευχάριστο ήχο σα να σκάει κάποια φούσκα. Θα πρέπει να ενθαρρύνουμε τους μαθητές να χρησιμοποιήσουν δικές τους λέξεις για να περιγράψουν όποιο μοτίβο παρατηρούν. Όταν ένα μοτίβο παρατηρηθεί οι μαθητές πρέπει να το επεκτείνουν κάνοντας “κλικ” στο κουμπί με το ερωτηματικό και κλικάροντας στο σωστό χρώμα. Αν ολοκληρώσουν με επιτυχία την άσκηση, επιβραβεύονται ( good job! ) και ακούγεται ένας ωραίος ήχος κάτι που κάνει ακόμα πιο ευχάριστο το παιχνίδι. Οι μαθητές έχουν την δυνατότητα να διορθώσουν το λάθος κάνοντας “κλικ” πάνω στο χρωματιστό κουμπί το οποίο γίνεται πάλι ερωτηματικό οπότε επιλέγουν άλλο χρώμα. Τέλος τσεκάρουν την απάντηση τους πατώντας check answer. Φυσικά μπορούν να συνεχίσουν με το επόμενο πρόβλημα και να παίξουν όσες φορές το επιθυμούν επιλέγοντας new problem.
Τι σχέση έχει με το Αναλυτικό Πρόγραμμα;:
Η δράση που προτείνω έχει άμεση σχέση με το Νέο Αναλυτικό Πρόγραμμα καθώς στόχος είναι να αναγνωρίζουν, να περιγράφουν και να συμπληρώνουν μοτίβα όπως αναφέρει και το νέο αναλυτικό πρόγραμμα στους στόχους του.
Να εντοπίζουν στοιχεία που λείπουν ή τα στοιχεία που είναι λάθος ακόμα και να καταμετρούν ποσότητες. Οι εκπαιδευτικοί μπορούν να συμβάλουν στην υλοποίηση των παραπάνω στόχων αξιοποιώντας το ψηφιακό υλικό της NVLM.
Εικόνες σχετικές με τη δράση:
Μοτίβα
Submitted by irida11 on Tue, 06/04/2013 - 01:33Χρονοπούλου Σπυριδούλα
Περίληψη:
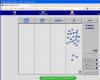
Στην συγκεκριμένη άσκηση επιλέγεται η μαθηματική έννοια του «Μοντέλου Χρωμάτων» (Color Patterns) και σκοπός είναι να δείξει στα παιδιά ότι τα μοντέλα ή αλλιώς πρότυπα είναι έννοιες που επαναλαμβάνονται, οπότε τα ίδια να καταστούν ικανά να μπορούν να αναγνωρίζουν και να περιγράφουν μοντέλα/πρότυπα. Παράλληλα, γίνεται χρήση Ηλεκτρονικού Υπολογιστή και κατάλληλης ηλεκτρονικής βιβλιοθήκης (μέσω προτεινόμενου ιστότοπου: http://nlvm.usu.edu/en/nav/topic_t_1.html).
Λογισμικά:
Τι μαθηματικά κάνω;:
Επιλέγεται η μαθηματική έννοια των «Άλγεβρας».
Πιο συγκεκριμένα, από αυτήν την μαθηματική έννοια επιλέγεται το «Μοντέλα Χρωμάτων» (Color Patterns).
H Επιλογή της συγκεκριμένης μαθηματικής έννοιας σκοπό να έχει να δείξει στα παιδιά ότι τα μοντέλα ή αλλιώς πρότυπα είναι πράγματα/έννοιες που επαναλαμβάνονται και να καταστήσουμε τα παιδιά ικανά να μπορούν να αναγνωρίζουν και να περιγράφουν μοντέλα/πρότυπα διότι η περιγραφή και η πρόβλεψη είναι πιο εύκολη με αυτόν τον τρόπο.
Οι μαθητές θα ωφεληθούν από την περιγραφή της ακολουθίας των χρωματιστών κύκλων, μιας και υπάρχει επαναλαμβανόμενη σειρά πραγματοποίησης (χρωματισμού) του γεγονότος. Συνεπώς, επιδιώκεται η ανάπτυξη της ικανότητας εύρεσης λύσης της συνέχειας στην ακολουθία χρωμάτων με στόχο την σταδικακή εισαγωγή τους στις μαθηματικές έννοιες της Άλγεβρας.
Τι δράση μπορώ να σχεδιάσω για τα παιδιά;:
1.Ζητείται από τα παιδιά να περιγράψουν μία ακολουθία/μοντέλο χρωμάτων. Συγκεκριμένα, ζητείται να παρατηρήσουν με ποιόν τρόπο και σειρά είναι τοποθετημένα οι χρωματισμένοι κύκλοι και με βάση αυτό να προβλέψουν τον χρωματισμό των επόμενων. Με λίγα λόγια να αναζητήσουν και να βρουν την διαδοχική τους ακολουθία.
2. Ερωτήσεις στα παιδιά:
α./ Τι χρώματα βλέπετε;
β./ Πόσα είναι τα χρώματα;
γ./ Τι σχήμα είναι χρωματισμένο;
δ./ Ποιό είναι το πρώτο χρώμα;
ε./ Ποιό είναι το δεύτερο χρώμα;
στ/ Ποιό είναι το επόμενο χρώμα κ.ο.κ.
3. Ζητώ από τα παιδιά να χρωματίσουν τα κενά πεδία με ένα χρώμα από τα προηγούμενα με τέτοιο τρόπο ώστε να ταιριάζει με εκείνα τα χρώματα που έχουν ήδη παρατηρήσει προηγουμένως. Επίσης, να κάνουν διάφορους συνδυασμούς που μέσω των διερευνήσεων θα καταλήξουν στο επιθυμητό αποτέλεσμα (βλ. Νέο Αναλυτικό Πρόγραμμα Σπουδών).
4. Ζητώ από τα παιδιά να παρατηρήσουν αν θα μπορούσε:
α. Να χρησιμοποιηθεί κάποιο άλλο χρώμα.
β. Κάθε πόσα πεδία έχουμε τη επανάληψη του ίδιου χρώματος.
γ. Αν υπάρχουν χρώματα στην παλέτα (δεξιά στήλη) που δεν έχουν χρησιμοποιηθεί έως τώρα.
5. Τα παιδιά είναι δυνατόν να διαμορφώσουν κάποιες υποθέσεις, όπως:
α. Τα χρώματα που χρησιμοποιούνται είναι μόνο τρία.
β. Η σειρά των χρωμάτων επαναλαμβάνεται.
6. Τα συμπεράσματα στα οποία μπορεί να οδηγηθούν τα παιδιά είναι πιθανόν:
α. Να δουν αν ο χρωματισμός που επέλεξαν είναι η σωστή λύση, κάτι που θα τους το πει είτε ο εκπαιδευτικός είτε η απάντηση από το τερματικό του ηλεκτρονικού υπολογιστή.
β. Αν δεν ακολουθηθεί η σωστή σειρά χρωματισμού, δεν θα υπάρχει η επιθυμητή λύση (κάτι που θα αποτυπωθεί με εμφάνιση ερωτηματικού ή άλλου συμβόλου στην οθόνη του Η/Υ).
γ. Πρέπει να χρησιμοποιούν μόνον τα χρώματα που ήδη υπάρχουν διαθέσιμα.
δ. Πρέπει να ακολουθείται η άλληλουχία του χρωματισμού, με την ίδια συχνότητα.
ε. Για να υπάρξει τέλος της άσκησης, θα πρέπει να έχουτν χρωματισθεί σωστά όλοι τα σύμβολα (κύκλοι).
Τι σχέση έχει με το Αναλυτικό Πρόγραμμα;:
H συγκεκριμένη προτεινόμενη δράση της περιγραφής ενός Μοντέλου Χρωμάτων, καταλήγει να αναδυκνύει πολλές από τις πτυχές που αναφέρονται μέσα στο Νέο Αναλυτικό Πρόγραμμα και ειδικότερα:
α. Ανάπτυξη βασικών ικανοτήτων των παιδιών όπως της επικοινωνίας, της δημιουργικής και κριτικής σκέψης, προσωπικής ταυτότητας και αυτονομίας και των κοινωνικών ικανοτήτων.
β. Εντός ευέλικτων μαθησιακών περιβάλλοντων (σύμφωνα με το Νέο Αναλυτικό Πρόγραμμα), οι εκπαιδευτικοί οργανώνουν μαθησιακές εμπειρίες αξιοποιώντας στη συγκεκριμένη περίπτωση το πλαίσιο των διερευνήσεων. (Σύμφωνα με το Νέο Αναλυτικό Πρόγραμμα), οι διευρευνήσεις μπορεί να λάβουν τη μορφή μιας μικρής χρονικά έρευνας, ενός σχεδίου εργασίας (όπως στην συγκεκριμένη περίπτωση) ή ενός προβλήματος που χρειάζεται άμεσα επίλυση.
γ. Στην συγκεκριμένη δράση, η μάθηση των παιδιών επέρχεται τόσο μέσω της δικής τους προσπάθειας (δοκιμή-σφάλμα) όσο και μέσω της καθοδήγησης/συμμετοχής του εκπαιδευτικού, με την παρότρυνση και την υποστήριξη του ακόμη και στις περιπτώσεις εκτέλεσης λάθους από την πλευρά των παιδιών. Σύμφωνα με το Νέο Αναλυτικό Πρόγραμμα, συνήθως τα παιδιά δείχνουν επιμονή κάνοντας συνεχείς ερωτήσεις για ότι τους προκαλεί το ενδιαφέρον και προσπαθούν να δοκιμάσουν καινούργια πράγματα και να επιλύσουν προβλήματα. Οι εκπαιδευτικοί διατυπώνουν κατάλληλες ερωτήσεις που ενεργοποιούν την δημιουργική σκέψη και φαντασία των παιδιών και αποτελούν πρόκληση για αυτά. (π.χ. τι θα μπορούσε να συμβεί αν, πώς θα μπορούσαμε να μάθουμε πως-που-τι, αναρωτιέμαι γιατί συμβαίνει αυτό). Οι εκπαιδευτικοί προτείνουν εναλλακτικές λύσεις ή στρατηγικές και αφήνουν τα παιδιά να επιλέξουν.
δ./ Η προτεινόμενη δράση της περιγραφής ενός Μοντέλου Χρωμάτων εμπίπτει στην κατηγορία του Νέου Αναλυτικού Πρόγραμματος των παιχνιδιών με κανόνες. Ειδικότερα, αναφέρεται στο λογισμικό εκπαιδευτικών παιχνιδιών και δραστηριοτήτων με πολυμέσα για προσχολική και πρώτη σχολική ηλικία.
ε./ Τέλος, η προτεινόμενη δράση εμπίπτει στην κατηγορία του Νέου Αναλυτικού Πρόγραμματος
Με βάση την προηγηθείσα ανάλυση, συνοψίζοντας αναφέρεται ότι λάμβάνει χώρα η επιλογή της μαθηματικής έννοιας των «Αριθμών και Πράξεων» (Numbers and Operations) και πιο συγκεκριμένα, εκείνης του «Μοντέλου Χρωμάτων» (Color Patterns). Σκοπός της εν λόγω δράσης είναι να δείξει στα παιδιά ότι τα μοντέλα ή αλλιώς πρότυπα είναι πράγματα/έννοιες που επαναλαμβάνονται, ενώ παράλληλα στόχος είναι να καταστήσουμε τα παιδιά ικανά να μπορούν να αναγνωρίζουν και να περιγράφουν μοντέλα/πρότυπα διότι η περιγραφή και η πρόβλεψη φαίνεται να είναι πιο εύκολη με αυτόν τον τρόπο.
Τα παιδιά αναμένεται να ωφεληθούν από την περιγραφή της ακολουθίας των χρωματιστών κύκλων, μιας και υπάρχει επαναλαμβανόμενη σειρά πραγματοποίησης (χρωματισμού) του γεγονότος. Συνεπώς, επιδιώκεται η ανάπτυξη της ικανότητας εύρεσης λύσης της συνέχειας στην ακολουθία χρωμάτων με στόχο την σταδικακή εισαγωγή τους στις μαθηματικές έννοιες (στην περίπτωση μας της Άλγεβρας).
Τέλος, γίνεται σύνδεση της εν λόγω δράσης με συγκεκριμένα πεδία του Νέου Αναλυτικού Πρόγραμματος Σπουδών για το Νηπιαγωγείο όπως άλλωστε ζητείται και από την εκφώνηση της άσκησης.
Εικόνες σχετικές με τη δράση:
