Αναγνωρίζω, αναλύω και αντιγράφω μοτίβα
Submitted by trikka on Mon, 06/17/2013 - 17:34
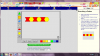
Καθώς η ομάδα παιδιών και εγώ βρισκόμαστε γύρω από τον υπολογιστή και παρατηρούμε τα δεδομένα της οθόνης, εφιστώ την προσοχή των μαθητών σε ένα συγκεκριμένο σχήμα που προβάλλεται. Τα παιδιά αναλύουν το σχήμα αυτό σε γεωμετρικά σχήματα και σε χρώματα, μετράνε και αθροίζουν τα επιμέρους αυτά σχήματα, και τέλος «διαβάζουν» τον τρόπο με τον οποίο αυτά είναι διαταγμένα κάνοντας έτσι την αναγνώριση του μοτίβου του αρχικού σχήματος. Με γνώμονα αυτή την ανάλυση τα παιδιά δημιουργούν ένα αντίγραφο του αρχικού σχήματος κοντά σε αυτό επαληθεύοντας τα δεδομένα που αναγνώρισαν προηγουμένως.
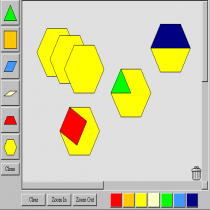
Από τον Άξονα Μαθηματικών Εννοιών της Άλγεβρας επέλεξα τοVirtual Manipulative “Pattern Blocks”. Το συγκεκριμένο Virtual Manipulative θεωρώ πως είναι ιδανικό για να εξασκηθούν τα παιδιά του νηπιαγωγείου στην αναγνώριση γεωμετρικών σχημάτων και χρωμάτων, στο μέτρημα, στην πρόσθεση, στην αντίληψη και αναπαραγωγή δεδομένων μοτίβων.
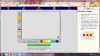
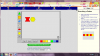
Αρχικά, αφού μαζέψω την ομάδα παιδιών γύρω από τον υπολογιστή, ανοίγοντας το VM αυτό, τα ρωτάω τι παρατηρούν σε αυτό που προβάλλεται στην οθόνη του υπολογιστή. Αφού, ίσως και με τη δική μου βοήθεια ή παρότρυνση, αναγνωρίσουν το μεγάλο ορθογώνιο πλαίσιο στο κέντρο, τα σχήματα που περιέχει μέσα και τα χρώματά τους, οδηγώ την προσοχή τους στην χρωματιστή εικόνα δεξιά της οθόνης. Πρώτα ζητώ να αναγνωρίσουν τα χρώματα που βλέπουν στο σχήμα της εικόνας αυτής. Έπειτα τους λέω να παρατηρήσουν το προβαλλόμενο σχήμα (Α). Μήπως αναγνωρίζετε μέσα σε αυτό γνωστά σας γεωμετρικά σχήματα; Αυτά τα σχήματα έχουν ίδιο ή διαφορετικό χρώμα μεταξύ τους; Ποια έχουν κόκκινο και ποια κίτρινο χρώμα; Αφού γίνει η αναγνώριση των σχημάτων και των χρωμάτων τους, τα παιδιά μπορούν να μετρήσουν πλέον πόσα είναι τα τραπέζια της εικόνας και πόσα τα εξάγωνα. Μετά τους ρωτώ πόσα είναι όλα τα σχήματα του σχεδίου Α. Για να αντιληφθούν καλύτερα το εικονιζόμενο μοτίβο παροτρύνω να περιγράψουν το σχήμα Α που βλέπουν χρησιμοποιώντας τα μικρότερα γεωμετρικά σχήματα (τραπέζιο, εξάγωνο) και τη σειρά με την οποία αυτά παρουσιάζονται (από αριστερά προς τα δεξιά > δύο παραλληλόγραμμα το ένα πάνω στο άλλο, ένα εξάγωνο, δύο παραλληλόγραμμα το ένα πάνω στο άλλο, ένα εξάγωνο, δύο παραλληλόγραμμα το ένα πάνω στο άλλο, ένα εξάγωνο).
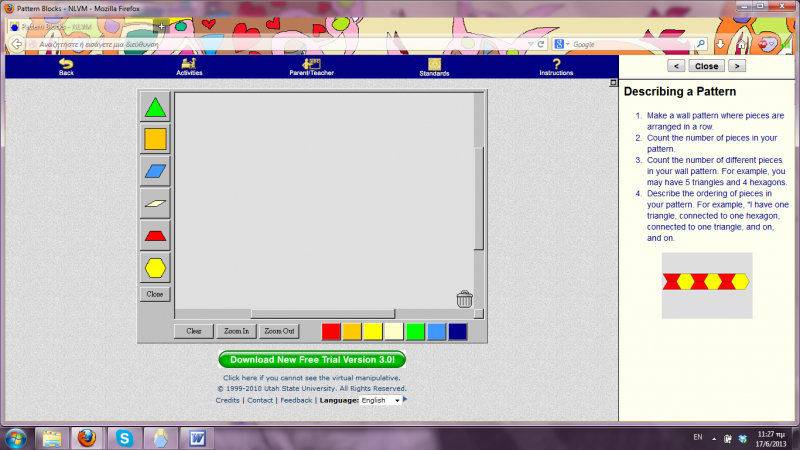
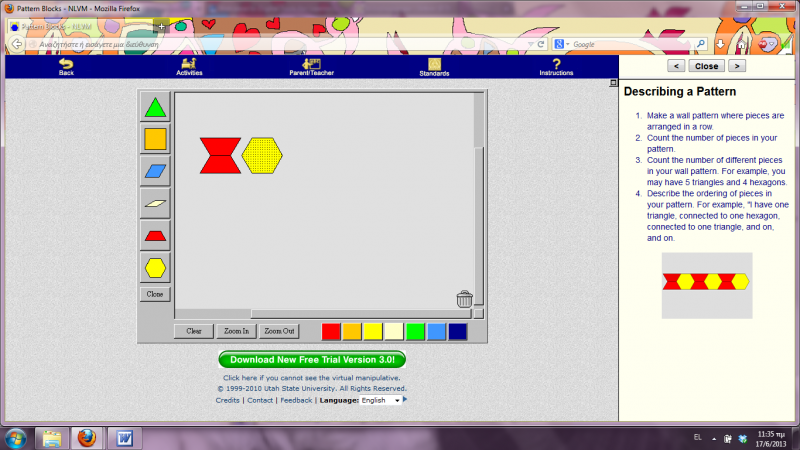
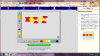
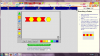
Αφού λοιπόν αναλύσαμε αρκετά το σχήμα Α δεξιά στην οθόνη, γυρνάμε στο κέντρο της και ζητώ από μεμονωμένα παιδιά να μου δημιουργήσουν με τα εργαλεία που γνωρίσαμε νωρίτερα το ίδιο μοτίβο Α θυμίζοντάς τους, όπου βρίσκουν δυσκολία, τα συμπεράσματα που αναφέραμε πριν για το μοτίβο αυτό (σχετικά με τα σχήματα που το απαρτίζουν, τα χρώματά τους, τη διάταξη και το πλήθος τους). Μετά την ορθή ολοκλήρωση της αντιγραφής του μοτίβου Α, μπορούμε να πατήσουμε το clear για να καθαρίσει η οθόνη και να έρθει ένα άλλο παιδί να επαναλάβει την άσκηση αυτή.
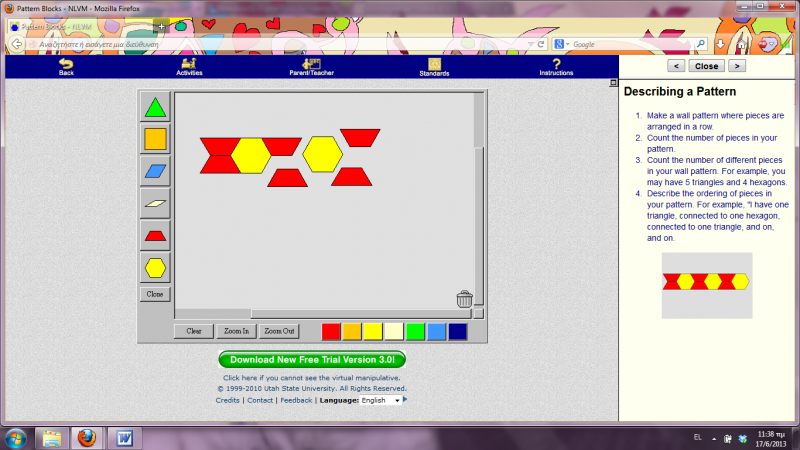
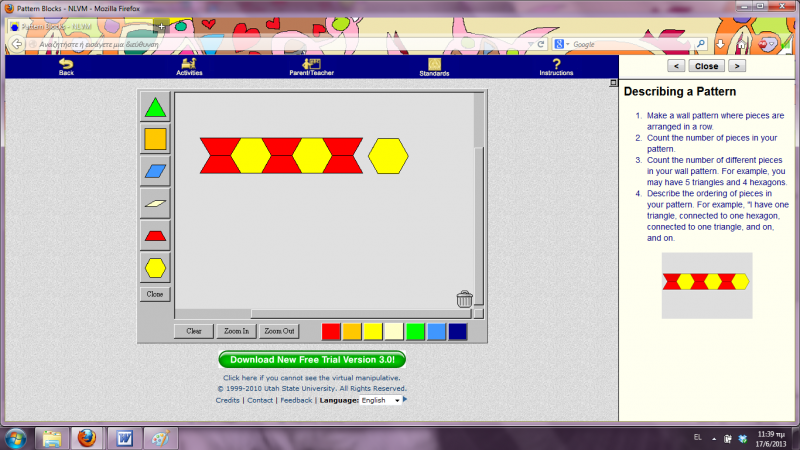
Απώτερος σκοπός είναι τα παιδιά να κατανοήσουν ότι ένα σχήμα που αρχικά μπορεί να φαίνεται άγνωστο, μπορεί να εμπεριέχει μέσα του γνωστά γεωμετρικά σχήματα τα οποία δημιουργούν ένα μοτίβο. Αν αυτό το μοτίβο αναγνωριστεί και αναλυθεί σωστά, τότε μπορούμε να δημιουργήσουμε μόνοι μας “κλώνους” του ίδιου σχήματος.
Με τη δράση αυτή, σύμφωνα με το Νέο Αναλυτικό Πρόγραμμα και την ενότητα Παιδί και Μαθηματικά (Πρόγραμμα Σχεδιασμού και Ανάπτυξης Δραστηριοτήτων Μαθηματικών) τα παιδιά εμπλέκονται σε καταστάσεις προβληματισμού και επεξεργάζονται σχήματα, χρώματα, σχέσεις, και αριθμούς. Προβληματίζονται πάνω στο μοτίβο Α , ερευνούν ποικίλες καταστάσεις, στηρίζονται σε προηγούμενες γνώσεις και εμπειρίες, κάνουν απλές υποθέσεις και καταλήγουν σε σχετικά συμπεράσματα. Τους δίνεται η ευκαιρία να παρατηρήσουν, να περιγράψουν, να συγκρίνουν και να ταξινομήσουν με βάση ορισμένα γνωρίσματα που είναι κοινά στα αντικείμενα της δράσης μας. Αναγνωρίζουν και ονομάζουν γεωμετρικά σχήματα, απαριθμούν αντικείμενα, βάζουν τα σχήματα στη σειρά και έτσι εξοικειώνονται με τα τακτικά αριθμητικά. Ενθαρρύνονται να αντιλαμβάνονται και να αναπαράγουν δεδομένα μοτίβα. Τέλος, τα παιδιά μαθαίνουν πώς να αξιοποιούν την τεχνολογία και εξοικειώνονται με αυτή.