Η Γεωμετρία της χελώνας
Submitted by chnalmpa on Sun, 06/16/2013 - 16:52
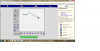
Επιλέγω το συγκεκριμένο virtual manipulative από τον άξονα γεωμετρίας. Μέσα από το συγκεκριμένο virtual manipulative επιδιώκω τα παιδιά να εξερευνήσουν τους αριθμούς, τα σχήματα, και τη λογική του προγραμματισμού με την οποία μπορεί να κινηθεί μια χελώνα.

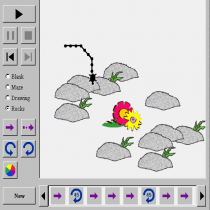
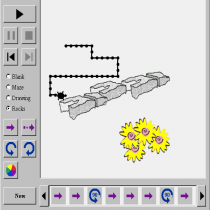
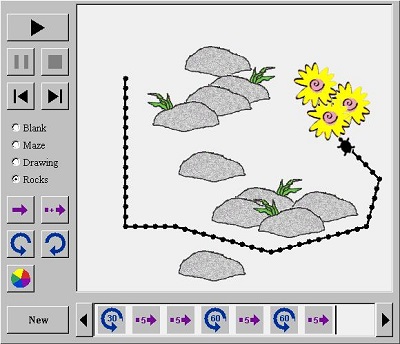
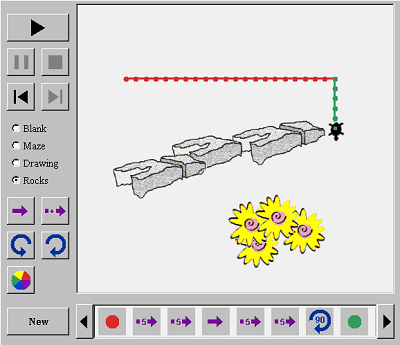
Χρησιμοποιώ το Turtle Geometry από την άξονα της γεωμετρίας. Στην οποία τα παιδιά μπορούν να κάνουν ένα σχέδιο για τη θαλάσσια χελώνα, να δοκιμάσουν το σχέδιό τους, να αλλάξουν το σχέδιό τους και να δουν ένα λαβύρινθο, μια εικόνα ή βράχια.
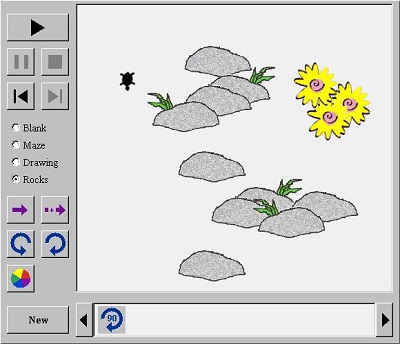
1.Αρχικά ζητάω από τα παιδιά να παρατηρήσουν την εικόνα που βλέπουν μπροστά τους και να την περιγράψουν. Επομένως να μου πουν τις σκέψεις τους σχετικά με το τι μπορεί να ζητάει αυτή η άσκηση.
2.Για να κατευθύνω την σκέψη των παιδιών κάνω κάποιες ενδεικτικές ερωτήσεις:
- Τι μπορούμε να κάνουμε για να μετακινήσουμε τη χελώνα;
-Τι έκανες πρώτα και ήρθε μέχρι εδώ η χελώνα;
-Τι έκανες μετά για να αλλάξει την κατεύθυνση της;
-Τι σκέφτεσαι να κάνεις τώρα;
-Τι θα άλλαζε αν πατούσες στο κουμπί με τα χρώματα;
-Τι συνέβη όταν πάτησες στο κουμπί που έχει τα χρώματα;
-Αν ξαναπατούσαμε σ’ αυτό (το κουμπί)τι λες να γινόταν;
3. Ζητάω από τα παιδιά να πειραματίζονται με τους εξής τρόπους:
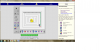
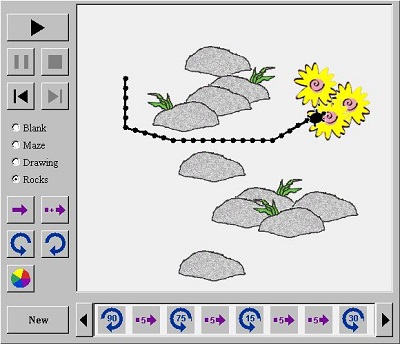
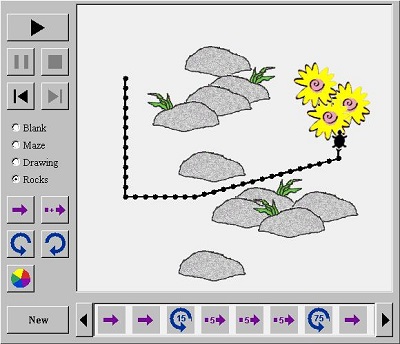
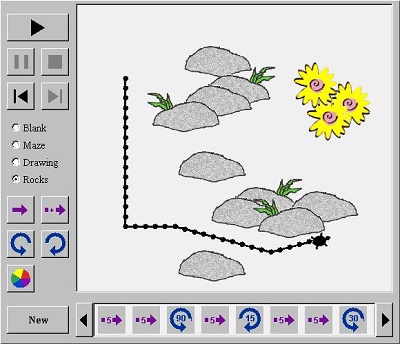
Να κάνουν ένα σχέδιο για τη θαλάσσια χελώνα:
Μπορούν να δώσουν ένα σχέδιο στη χελώνα μετακινώντας τη σειρά του, και να αλλάξουν το χρώμα της διαδρομής. Πρώτα να κάνουν ένα σχέδιο, στη συνέχεια, να το δοκιμάσουν, και να το αλλάξουν. Χρησιμοποιήσουν αυτά τα κουμπιά για να κάνουν ένα σχέδιο:  για την μετακίνηση προς τα εμπρός,
για την μετακίνηση προς τα εμπρός,
 για τη μετακίνηση προς τα εμπρός για περισσότερο από ένα χώρο,
για τη μετακίνηση προς τα εμπρός για περισσότερο από ένα χώρο,
 για να στρίψουν αριστερά
για να στρίψουν αριστερά
 για να στρίψουν δεξιά
για να στρίψουν δεξιά
 για να αλλάξουν το χρώμα της διαδρομής της χελώνας.
για να αλλάξουν το χρώμα της διαδρομής της χελώνας.
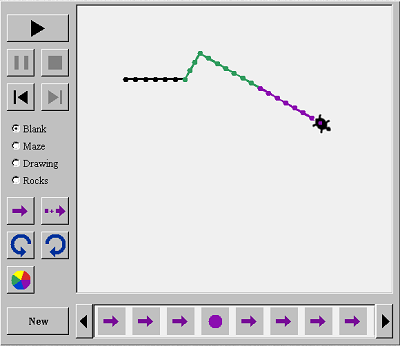
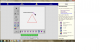
Να δοκιμάσουν το σχέδιό τους
Μετά να δοκιμάσουν το σχέδιό τους, χρησιμοποιώντας τα εξής κουμπιά:
 να εκτελέσουν το σχέδιο τους
να εκτελέσουν το σχέδιο τους
 να διακόπτουν τη λειτουργία
να διακόπτουν τη λειτουργία
 παύση της λειτουργίας
παύση της λειτουργίας
 να δημιουργήσουν αντίγραφα ασφάλεια σε μία θέση
να δημιουργήσουν αντίγραφα ασφάλεια σε μία θέση
 να εκτελέσουν ένα βήμα του σχεδίου τους
να εκτελέσουν ένα βήμα του σχεδίου τους
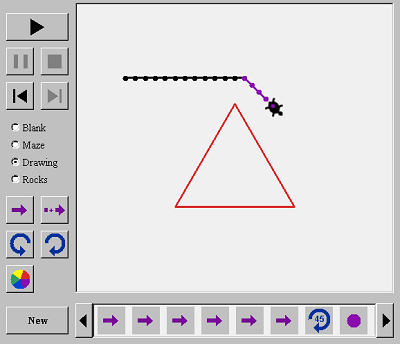
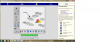
Να αλλάξουν το σχέδιο τους
Μετά τη δημιουργία ενός σχεδίου μπορεί να θέλουν να το αλλάξουν. Μπορούν να το κάνουν με την αφαίρεση ή την τροποποίηση των βημάτων όπως:
Α)Κάνοντας κλικ για το βήμα που θέλουν να αλλάξουν ή να καταργήσουν.
Β)Πατώντας το πλήκτρο Delete στο πληκτρολόγιο για να αφαιρέσουν το βήμα
Γ)Χρησιμοποιώντας το σχέδιο μωβ, μπλε, και τα κουμπιά σχέδιο χρώματος για να αλλάξουν το βήμα.
Μπορούν επίσης να προσθέτουν νέα μέτρα σε όλο το πρόγραμμα:
α. Κάνοντας κλικ ανάμεσα σε δύο βήματα.
β. Να χρησιμοποιήσουν στο σχέδιο μωβ, μπλε, με τα κουμπιά σχέδιο χρώματος επιλέγοντας το βήμα για να προσθέσουν.
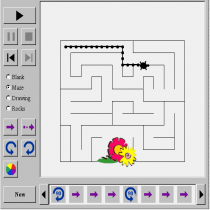
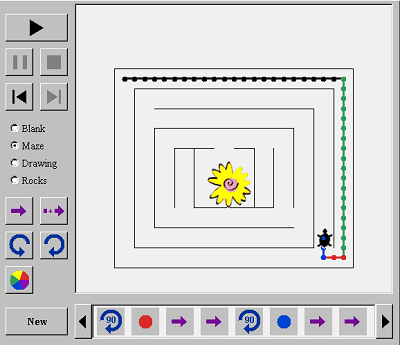
Να δοκιμάσουν ένα λαβύρινθο, μια εικόνα ή βράχια
Αφού έχουν μάθει λίγα πράγματα για το πώς να κάνουν σχέδια για τη θαλάσσια χελώνα, θα είναι διασκεδαστικό να προσθέσουν αντικείμενα που η χελώνα πρέπει να προσπαθήσει να τρέξει ανάμεσα σε αυτά. Χρησιμοποιώντας το κουμπιά Maze, Drawing, και Rocks να προσθέσουν τα εμπόδια στο σχέδιο τους.
4.Κάθε φορά που δοκιμάζουν μία από τα παραπάνω ζητάω από τα παιδιά να παρατηρούν τις διαφορές που έγιναν στο πλαίσιο. Αν έγινε κάποια αλλαγή στη διαδρομή, στο χρώμα της διαδρομής που έκανε η χελώνα. Επομένως θέλω να παρατηρούν αν κατά τη διάρκεια των πειραματισμών άλλαξε η χελώνα μέγεθος και χρώμα.
5.Τα παιδιά μπορούν να υποθέτουν ότι η χελώνα είναι δικιά τους, ή ψάχνει τον φίλο του και εμείς πρέπει να την κατευθύνουμε σωστά για να τον βρει, ή έχει χαθεί και δεν μπορεί να βρει τη θάλασσα και άλλα..
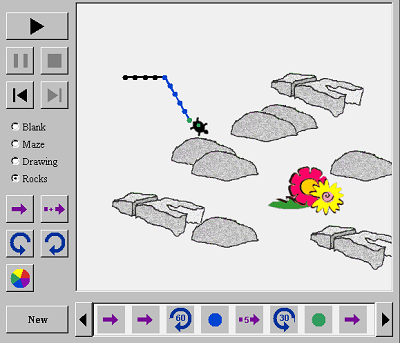
Το συγκεκριμένο virtual manipulative επιζητά την ενεργή δράση των ατόμων που εμπλέκονται γιατί έχουν ένα κίνητρο και ένα στόχο να πραγματοποιήσουν, δράση έχει μαθηματικά χαρακτηριστικά όπως είναι η διερεύνηση μέσα από τη χρήση εργαλείων και πηγών, η ανάπτυξη στρατηγικών επίλυσης προβλημάτων, η ανάπτυξη και χρήση τεχνικών, η δημιουργία εννοιολογικών συνδέσεων, η σύνδεση αναπαραστάσεων, η ανάπτυξη συλλογισμού. Επίσης η εξερεύνηση των αριθμών, των σχημάτων, και τη λογική του προγραμματισμού.