Προσυλλογιστική περίοδος (3-6 έτη)- Χαρακτηριστικά της σκέψης του νηπίου: Το νήπιο, συγκρινώμενο με το βρέφος, παρουσιάζει καταφανή νοητική υπεροχή. Έχει ξεπεράσει την ηλικία της πραξιακής αναπαράστασης και προσαρμογής. Αρχίζει να εισέρχεται στη περίοδο της συμβολικής- παραστατικής λειτουργίας και της λογικής διανόησης που αποτελεί γνώρισμα αποκλειστικό της ανθρώπινης νοημοσύνης. Συγκρινόμενο όμως το νήπιο με παιδιά μεγαλύτερης ηλικίας και με τον ώριμο ενήλικο, παρουσιάζει πλείστες και σημαντικές νοητικές ατέλειες. (Εξελικτική ψυχολογία, Παρασκευοπούλου Ι., τόμος 1,2, σελ 34). Συγκεκριμένα, η σκέψη του νηπίου είναι εγωκεντρική, επικεντρώνεται σε ένα μόνο χαρακτηριστικό κάθε φορά και δεν έχει αντιστρεψιμότητα.

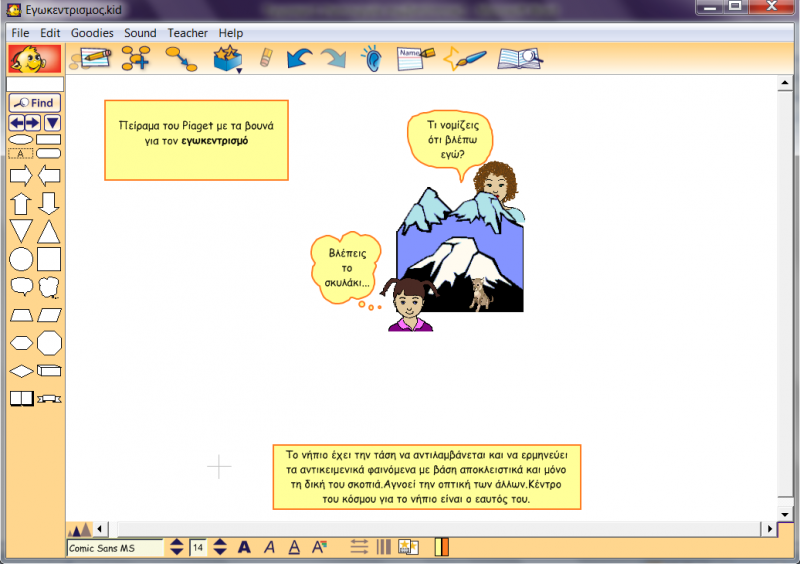
Η σκέψη του νηπίου είναι εγωκεντρική: Το νήπιο έχει την τάση να αντιλαμβάνεται και να ερμηνεύει τα αντικειμενικά φαινόμενα με βάση αποκλειστικά και μόνο την προσωπική, τη δική του σκοπιά. Είναι ανίκανο να πάρει θέση – το ρόλο – άλλου προσώπου, να κατανοήσει την άποψη κάποιου άλλου, να θεωρήσει ότι η δική του άποψη είναι μια από άλλες πιθανές απόψεις. Δεν πρόκειται για εγωισμό, για υπερτροφία του Εγώ, που είναι συνειδητό φαινόμενο ηθικής τάξης, αλλά για μια γνωστική αδυναμία του νηπίου, μια ασύνειδη τάση να μεταφράζει τα πάντα με βάση τα προσωπικά του βιώματα. Κέντρο του κόσμου για το νήπιο είναι ο εαυτός του. (Εξελικτική ψυχολογία, Παρασκευοπούλου Ι., τόμος 1,2, σελ.36)

Ο Piaget αναφέρει το εξής χαρακτηριστικό πείραμα που φανερώνει τοπικό εγωκεντρισμό: Παρουσίαζε στο παιδί μικροπλάσματα τριών βουνών τοποθετημένα επάνω σε ένα τραπέζι. Το παιδί ενθαρρυνόταν να κινείται γύρω από το τραπέζι και έτσι να παρατηρεί τον ορεινό όγκο από διάφορες θέσεις και προοπτικές. Στη συνέχεια, έβαζε το παιδί να καθίσει σε μια ορισμένη θέση (θέση Α) και μια κούκλα σε διαφορετικά σημεία γύρω από το τραπέζι (στη θέση Β, στη θέση Γ, στη θέση Δ). Ζητούσε από το παιδί να επιλέξει από 10 φωτογραφίες, τη φωτογραφία ου έδειχνε πως έβλεπε η κούκλα τα βουνά κάθε φορά. Ζητούσε δηλαδή από το παιδί να «μεταφερθεί» στη θέση της κούκλας, να αγνοήσει τη δική του άποψη. Διαπιστώθηκε ότι τα παιδιά 4 ετών και κάτω επιλέγουν συστηματικά τη φωτογραφία που δείχνει πώς βλέπει το ίδιο το παιδί τον ορεινό όγκο. Ήταν εντελώς ανυποψίαστα ότι η κούκλα μπορούσε να έχει διαφορετική άποψη από ότι εκείνα. (Εξελικτική ψυχολογία, Παρασκευοπούλου Ι., τόμος 1,2, σελ 36-38).

Η σκέψη του νηπίου επικεντρώνεται σε ένα μόνο χαρακτηριστικό κάθε φορά: Η σκέψη του νηπίου προσκολλάται κάθε φορά σε ένα μόνο χαρακτηριστικό του προβλήματος και αγνοεί άλλα σημαντικά. Η προσοχή του συγκεντρώνεται σε ένα μόνο στοιχείο, σε μια μόνο πλευρά του προβλήματος, και δεν συνυπολογίζει άλλες ουσιώδεις. Το χαρακτηριστικό το οποίο αιχμαλωτίζει την προσοχή του παιδιού είναι συνήθως ένα περίοπτο αντιληπτικό στοιχείο, που στιγμιαία κυριάρχησε στην αντίληψη του παιδιού. Η μονοσήμαντη αυτή αντιμετώπιση της πραγματικότητας οδηγεί, όπως είναι φυσικό, σε αντιφάσεις και ασυνέπειες.(Εξελικτική ψυχολογία, Παρασκευοπούλου Ι., τόμος 1,2, σελ39)

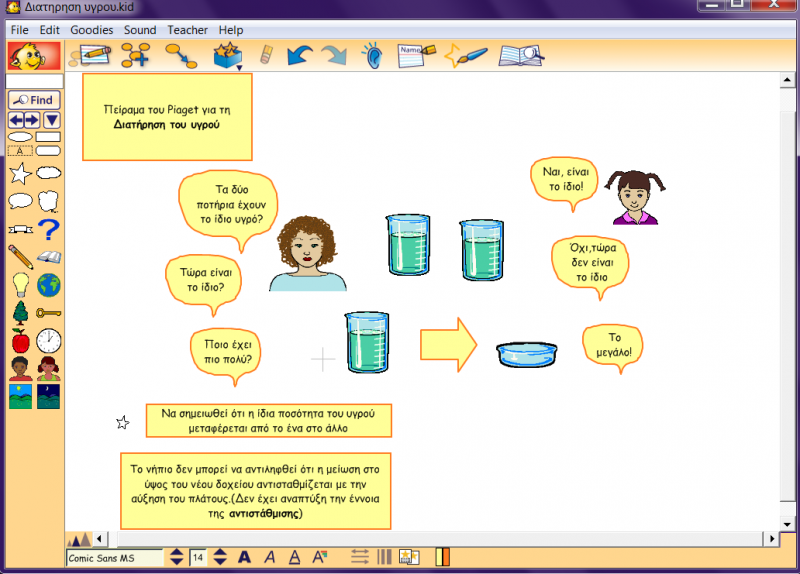
Ας εξετάσουμε ένα γνωστό πείραμα του Piaget για τη διατήρηση του υγρού: Δείχνουμε στο παιδί δύο όμοια ποτήρια με το ίδιο ποσό υγρού στο καθένα. Το παιδί μας διαβεβαιώνει ότι πράγματι και στα δύο ποτήρια υπάρχει η ίδια ποσότητα υγρού. Στη συνέχεια, μπροστά στο παιδί, αδειάζουμε το υγρό από ένα ποτήρι σε ένα πλατύ- κοντό ποτήρι. Το παιδί αρνείται ότι υπάρχει στα δύο ποτήρια η ίδια ποσότητα υγρού. Θα δηλώσει ή ότι στο στενό-υψηλό ποτήρι υπάρχει περισσότερο υγρό, γιατί η στάθμη του υγρού είναι υψηλότερη ή, ότι στο πλατύ-κοντό ποτήρι υπάρχει περισσότερο νερό, γιατί είναι πιο πλατύ. Η μια ή η άλλη απάντηση θα εξαρτηθεί από το ποιο χαρακτηριστικό θα κυριαρχήσει στην αντίληψή του: το ύψος ή το πλάτος. Το παιδί της προσχολικής ηλικίας δεν είναι ικανό να αντιληφθεί τον εξισορροπητικό ρόλο που μπορεί να διαδραματίσει η αλλαγή ενός άλλου στοιχείου. Σκέπτεται με βάση ένα μοναδικό αντιληπτικό στοιχείο και αλλοιώνει την πραγματικότητα. (Εξελικτική ψυχολογία, Παρασκευοπούλου Ι., τόμος 1,2 σελ39)

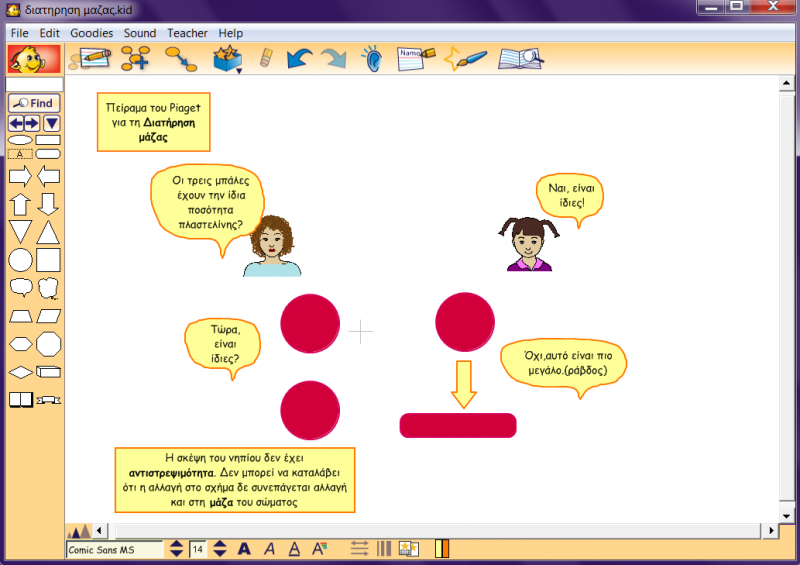
Πείραμα του Piaget για τη Διατήρηση της μάζας: Αντιφατικές απαντήσεις θα μας δώσει επίσης το νήπιο και στην εξής πειραματική κατάσταση: Του παρουσιάζουμε τρεις βώλους πλαστελίνης του ίδιου σχήματος, μεγέθους και χρώματος. Το παιδί αναγνωρίζει και μας βεβαιώνει ότι και οι τρεις βώλοι έχουν την ίδια ποσότητα πλαστελίνης. Στη συνέχεια, μπροστά στο παιδί, μεταπλάθουμε το δεύτερο βώλο σε κυλινδρικό και τον τρίτο τον χωρίζουμε σε μικρότερους βώλους. Το παιδί ισχυρίζεται ότι η ποσότητα πλαστελίνης στο δεύτερο και στον τρίτο βώλο έγινε περισσότερη ή λιγότερη, στηριζόμενο σε μια μονομερή αντιληπτική άποψη (το μήκος, το πλάτος, το πλήθος), χωρίς να μπορεί να συνυπολογίσει ταυτόχρονα τον αντισταθμιστικό ρόλο των άλλων δεδομένων του προβλήματος. Το νήπιο, κατά την ορολογία του Piaget, δεν μπορεί να «αποκεντρωθεί» (decenter), να μην εστιάζει σε ένα μοναδικό στοιχείο, να συνυπολογίζει πολλές διαστάσεις συγχρόνως και να εξετάζει την αλληλεπίδραση τους.(Εξελικτική ψυχολογία, Παρασκευοπούλου Ι., τόμος 1,2, σελ40). Το ίδιο πείραμα χρησιμοποιεί για να δείξει ότι η σκέψη του νηπίου δεν έχει αντιστρεψιμότητα.

Συναφές προς το φαινόμενο της επικέντρωσης είναι και το ότι το νήπιο αντιλαμβάνεται τα συμβαίνοντα μόνο σε στατικές καταστάσεις, σε διαδοχικές σαφώς διαχωρισμένες καταστάσεις, και όχι σε αλληλένδετους μετασχηματισμούς. Δεν έχει την εσωτερική ευελιξία να βασίσει τη σκέψη του στις αλλαγές, αλλά μόνο στο αποτέλεσμα. Δεν μπορεί να συνδέει τις διαδοχικές φάσεις σε ένα όλο με συνοχή. Να συλλάβει ταυτόχρονα, σε μια εσωτερική επιτομή, μια πλήρη σειρά διαδοχικών συμβάντων. Τα βλέπει σαν κινηματογραφική ταινία σε βραδεία κίνηση που κάθε σκηνή εμφανίζεται ως ξεχωριστή φωτογραφία. Δεν μπορεί να αναπαραστήσει ένα σύνθετο γεγονός ή αντικείμενο, συσχετίζοντας τα μέρη του με το όλο. Άλλοτε συγκεντρώνει την προσοχή του σε επιμέρους στατικά στοιχεία και άλλοτε αντιμετωπίζει το γεγονός σαν ένα αδιαφοροποίητο σύνολο. Η γνωστική αυτή αδυναμία το νηπίου λέγεται συγκρητισμός. (Εξελικτική ψυχολογία, Παρασκευοπούλου Ι., τόμος 1,2, σελ 40)

Η σκέψη του νηπίου δεν έχει αντιστρεψιμότητα: Οι νοητικές ενέργειες των μεγαλύτερων παιδιών και των ενηλίκων μπορούν να κινούνται αμφιδρομικώς. Το παιδί της σχολικής ηλικίας π.χ., ενώ ακολουθεί μια σειρά νοητικών μετασχηματισμών, μπορεί, σε οποιαδήποτε στιγμή της διαδικασίας, να ακολουθήσει την αντίστροφή πορεία και να επανέλθει στο αρχικό σημείο, στο σημείο εκκίνησης. Μπορεί να αναπαριστά το «ξεδίπλωμα» μιας σειράς νοητικών ενεργειών, να παρακολουθεί τα προηγηθέντα στάδια μιας αλυσίδας σκέψεων και να την επανεξετάζει. (Εξελικτική ψυχολογία, Παρασκευοπούλου Ι., τόμος 1,2, σελ 41)

Το νήπιο όμως δεν έχει ακόμη αποκτήσει αμφιδρομικότητα στη σκέψη. Δεν μπορεί να αντιληφθεί ότι κάθε ενέργεια έχει και την αντίθετη της, την ενέργεια που την ακυρώνει, ότι κάθε ενέργεια εξισορροπείται από μια άλλη. Οι νοητικές του πράξεις δεν έχουν αναστρεψιμότητα, κατά την ορολογία του Piaget. Στο παράδειγμά μας με τη διατήρηση της ποσότητας του υγρού, αν το παιδί μπορούσε να απεικονίσει την αντίστροφη ενέργεια, δηλαδή το άδειασμα του υγρού πάλι στο αρχικό, το υψηλό-στενό ποτήρι, ή το αναπλάσημο του βώλου της πλαστελίνης από κυλινδρικό πάλι σε σφαιρικό, θα μπορούσε να αντιληφθεί τη διατήρηση της ποσότητας, την αμεταβλητότητα της ποσότητας, παρά τις εξωτερικές εμφανείς αλλαγές που επισυμβαίνουν. (Εξελικτική ψυχολογία, Παρασκευοπούλου Ι., τόμος 1,2, σελ 41)

Η πρώτη εμφάνιση της αναστρεψιμότητας των συλλογισμών αρχίζει περί το τέλος της προσχολικής ηλικίας. 6^ο έτος, και η κατάκτηση αποτελεί σημαντικό σταθμό στη νοητική ανάπτυξη του παιδιού. (Εξελικτική ψυχολογία, Παρασκευοπούλου Ι., τόμος 1,2, σελ 41)

Διαισθητική σκέψη: Μια μεταβατική περίοδος: Η νηπιακή ηλικία καλύπτει, όπως είδαμε και προηγουμένως, δύο επιμέρους περιόδους της νοητικής ανάπτυξης: την προεννοιολογική περίοδο (3^ο και 4^ο έτος) και τη διαισθητική περίοδο (5^ο και 6^ο έτος). (Εξελικτική ψυχολογία, Παρασκευοπούλου Ι., τόμος 1,2, σελ 41). Η διαισθητική περίοδος είναι μέρος της προσυλλογιστικής σκέψης, αλλά με έντονη παρουσία της συμβολικής λειτουργίας. Το παιδί παραμένει ακόμη δέσμιο των αντιληπτικών δεδομένων, πολλά όμως αρνητικά χαρακτηριστικά της προηγούμενης περιόδου (εγωκεντρισμός, μεταγωγικός συλλογισμός, έλλειψη αναστρεψιμότητας) αρχίζουν να παρακμάζουν. (Εξελικτική ψυχολογία, Παρασκευοπούλου Ι., τόμος 1,2, σελ 41). Τρεις βασικές λειτουργίες εμφανίζονται κατά τη διαισθητική περίοδο α) Η ικανότητα του παιδιού να σχηματίζει λογικές κατηγορίες, β) η ικανότητα να διακρίνει σχέσεις και γ) η ικανότητα να χειρίζεται αριθμητικές έννοιες. Έτσι το παιδί στη φάση αυτή μπορεί να ταξινομεί αντικείμενα με βάση κάποια ομοιότητά τους. Αν του δοθούν π.χ. διάφορα σχήματα θα προσπαθήσει να τα ταξινομήσει με βάση κάποιο κοινό χαρακτηριστικό τους, όπως π.χ. «πολύγωνα», «κυκλικά», «τετράγωνα», «τρίγωνα», «κύκλοι» κ.τ.ο. Ακόμη όμως στις ταξινομήσεις του χρησιμοποιεί μια μόνο διάσταση. Επίσης, το παιδί αρχίζει να διακρίνει σχέσεις ομοιότητας και διαφοράς, όπως π.χ. «Η κ. Ελένη είναι η μαμά του Γιώργου», «Το κουτάλι και το φτυάρι είναι όμοια», «Το γάλα είναι άσπρο, ο καφές είναι μαύρος». Ομοίως, το παιδί αρχίζει να χρησιμοποιεί αριθμούς και να τοποθετεί πράγματα σε ακολουθίες με βάση την ποσότητα τους (σειροθέτηση). Αρχίζει να αγνοεί ορισμένα εξωτερικά στοιχεία των πραγμάτων και να διαπιστώνει ότι υπάρχουν σχέσεις σε αριθμητική πλέον βάση. Μπορεί να αριθμήσει διάφορα πράγματα και να παράγει ένα άθροισμα διαφορετικών πραγμάτων. Μπορεί δηλαδή να κάνει αφαίρεση κάποιου κοινού χαρακτηριστικού μεταξύ διαφορετικών πραγμάτων και να χειρίζεται ως όμοια. (Εξελικτική ψυχολογία, Παρασκευοπούλου Ι., τόμος 1,2, σελ 41-42). Η διαισθητική περίοδος είναι ένα μεταβατικό στάδιο ανάμεσα στην προεννοιολογική σκέψη (3^ο και 4^ο έτος) και της προσυλλογιστικής περιόδου και στην περίοδο των συγκεκριμένων συλλογισμών (7^ο και 10^ο έτος). Ονομάζεται διαισθητική, γιατί το παιδί μπορεί «διαισθητικά», με μια συνολική θεώρηση του προβλήματος, να βρίσκει τη λογική λύση, χωρίς ακόμη να δείχνει ότι έχει επίγνωση της διαδικασίας που ακολούθησε, ή μπορεί τη διαδικασία αυτή να μας την περιγράψει γλωσσικώς. Αρχίζει δηλαδή να συμπεριφέρεται κατά τρόπο λογικό, όπως τα μεγαλύτερα παιδιά και οι ενήλικοι, αλλά δεν μπορεί ακόμη να μας δώσει πλήρη απολογισμό της πορείας που ακολουθεί κάθε φορά για να βρει τη σωστή λύση. (Εξελικτική ψυχολογία, Παρασκευοπούλου Ι., τόμος 1,2, σελ 42)

Το νήπιο δεν έχει αναπτύξει συμπερίληψη σε ομάδα, δεν κατηγοριοποιεί: Στην ηλικία των 4 ή 5 ετών, το νήπιο δεν έχει κατανοήσει την κατηγοριοποίηση πλήρως. Δεν έχει ακόμη αναπτύξει αυτό που ο Piaget αποκαλεί συμπερίληψη σε ομάδα (class inclusion). Σε ένα κλασικό πείραμα του ο Piaget έδινε ξύλινες χάντρες, από τις οποίες οι περισσότερες ήταν καφέ και λίγες ήταν άσπρες. Παιδιά 5 ή 6 ετών δεν μπορούσαν να αντιληφθούν τη σχέση «όλες οι χάντρες είναι ξύλινες». Ότι δηλαδή τόσο οι καφέ όσο και οι άσπρες χάντρες περιλαμβάνονται στην ευρύτερη ομάδα που είναι οι «ξύλινες χάντρες». Έτσι, όταν το παιδί ερωτηθεί: «Οι καφέ χάντρες είναι περισσότερες ή οι ξύλινες χάντρες;» απαντά ότι περισσότερες είναι οι «καφέ χάντρες». Κάνει αυτό το λάθος, γιατί συγκρίνει τις «καφέ χάντρες» με την παράλληλη ομάδα «άσπρες χάντρες». Δεν μπορεί ακόμη να αντιληφθεί συγχρόνως το όλο (ξύλινες χάντρες) και τα μέρη (άσπρες χάντρες, καφέ χάντρες), γιατί δεν έχει αναπτύξει την έννοια της συμπεριληπτικής ταξινόμησης. (Εξελικτική ψυχολογία, Παρασκευοπούλου Ι., τόμος 1,2 σελ 48).

Πείραμα του Piaget για τη συμπερίληψη στην ομάδα:

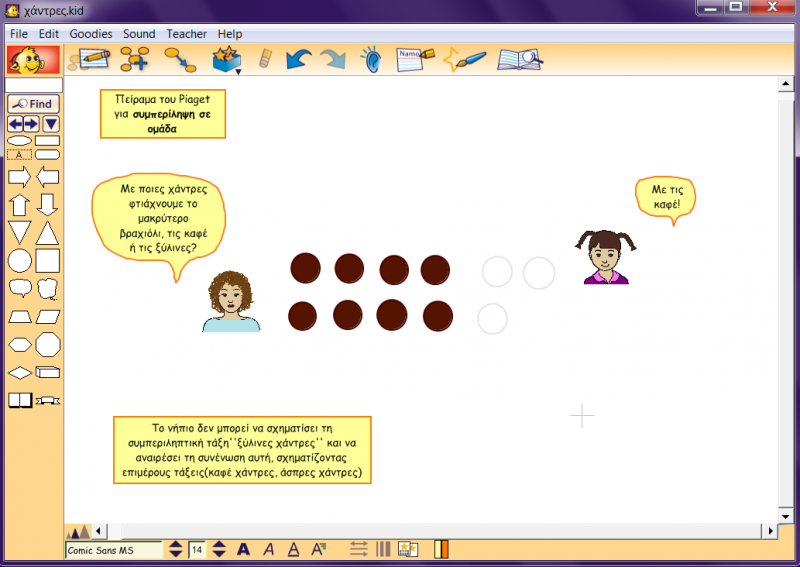
Διαστάσεις κατηγοριοποίησης: Κάθε πράγμα θεωρικά έχει άπειρα χαρακτηριστικά που μπορεί το άτομο να διαφοροποιήσει και να γενικεύσει. Καθετί στα πράγματα, το οποίο μπορεί το άτομο να αντιληφθεί με τις αισθήσεις του ή νοητικά να συλλάβει, είναι δυνατό να αποτελέσει «διάσταση» και κατηγοριοποίηση. (Εξελικτική ψυχολογία, Παρασκευοπούλου Ι., τόμος 1,2, σελ 49)

Κύρια είδη χαρακτηριστικών-διαστάσεων που χρησιμοποιούνται στην κατηγοριοποίηση είναι:

α) Φυσικές ιδιότητες: Το χρώμα, το μέγεθος, το σχήμα, το υλικό κατασκευής, η σύνθεση, ο παραγόμενος ήχος, οι τυπικές κινήσεις.

β) Λειτουργικά χαρακτηριστικά: Ό, τι μπορεί να κάνει ή ό, τι μπορεί να γίνει το αντικείμενο κάτω από ορισμένες καταστάσεις, όπως π.χ. «φαγώσιμο», «φορητό», «το χρησιμοποιούν τα παιδιά», «το χρησιμοποιούν για γράψιμο».

γ) Σχέσεις σε ένα γενικότερο σύστημα σχέσεων: π.χ. «ανεψιός», «πρωταθλητής», «πρώτος-τελευταίος»

Το παιδί της προσχολικής ηλικίας χρησιμοποιεί τα δύο πρώτα είδη διαστάσεων: τα αντικείμενα τα ορίζει με τα αντιληπτικά τους στοιχεία και τις λειτουργίες τους. Με την είσοδο του παιδιού στο σχολείο θα αρχίσει η κατανόηση και η χρησιμοποίηση σχέσεων μέσα σε ένα γενικότερο σύστημα σχέσεων. (Εξελικτική ψυχολογία, Παρασκευοπούλου Ι., τόμος 1,2, σελ 49)

Ειδικότερα, σχετικά με την προτίμηση των διαφόρων φυσικών ιδιοτήτων των αντικειμένων, έχει διαπιστωθεί ότι το νήπιο αρχικά (3^ο έτος) προτιμά το χρώμα και αγνοεί τα άλλα χαρακτηριστικά. Αν του δοθούν π.χ. μερικά κόκκινα και πράσινα τρίγωνα και μερικοί κόκκινοι και πράσινοι κύκλοι, η αυθόρμητη ταξινόμηση που θα χρησιμοποιήσει είναι μια ομάδα με τα πράσινα (τρίγωνα και κύκλους) και μια άλλη με τα κόκκινα (τρίγωνα και κύκλους). Αγνοεί το σχήμα. Δεύτερο σε προτίμηση έρχεται το μέγεθος. Αντίθετα, το σχήμα γίνεται κυρίαρχο χαρακτηριστικό στο 6^ο έτος της ηλικίας. (Εξελικτική ψυχολογία, Παρασκευοπούλου Ι., τόμος 1,2, σελ 49)

Συγκεκριμένης λογικής νόησης (7-11 έτη): Με την εμφάνιση της συμβολικής λειτουργίας το νήπιο αποκτά για πρώτη φορά τη δυνατότητα για εσωτερίκευση των εξωτερικών του δράσεων. Οι εσωτερικοποιημένες όμως αυτές πράξεις της νηπιακής ηλικίας δεν είναι αληθείς λογικές πράξεις, γιατί, η εσωτερικοποίηση δεν είναι το μόνο γνώρισμα των λογικών πράξεων. Για να χαρακτηρισθεί μια πράξη ως λογική, πρέπει, συγχρόνως με την εσωτερίκευση να έχει και άλλα χαρακτηριστικά, π.χ. αντιστρεψιμότητα. (Εξελικτική ψυχολογία, Παρασκευοπούλου Ι., τόμος 3,4, σελ 43-44). Οι λογικές πράξεις γίνονται με βάση ορισμένους λογικούς κανόνες. Από τους κανόνες αυτούς οι σημαντικότεροι είναι οι δυο κανόνες της αναστρεψιμότητας (reversibility): η αναίρεση και η αντιστάθμιση. Σύμφωνα με τον κανόνα της αναίρεσης (inversion), μια λογική πράξη μπορεί να διεκπεραιωθεί νοητικά προς την αντίθετη κατεύθυνση και έτσι να ακυρωθεί, να απαλειφθεί. Το παιδί ενώ συνενώνει τις πρωτογενείς τάξεις για να σχηματίσει τη συμπεριληπτική τάξη, γνωρίζει συγχρόνως ότι μπορεί, εκτελώντας την αντίθετη πράξη (αφαίρεση αντί πρόσθεσης), να παραγάγει από τη συμπεριληπτική τάξη τις πρωτογενείς τάξεις και το αντίστροφο. (Αυτό φαίνεται και στο πείραμα του Piaget με τις «ξύλινες χάντρες») (Εξελικτική ψυχολογία, Παρασκευοπούλου Ι., τόμος 3,4, σελ 44).

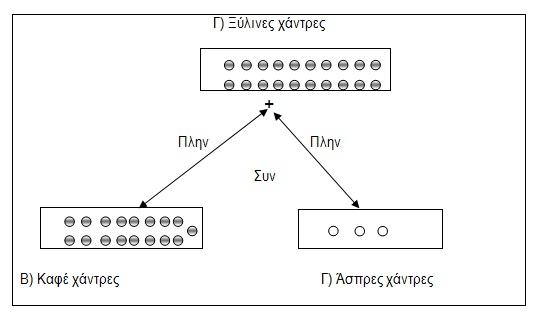
Σχηματική παράσταση της συναγωγής των αναστρέψιμων νοητικών πράξεων για την επίλυση του πειράματος του Piaget με τις ξύλινες χάντρες: Δίνονται στο παιδί 17 καφέ και 3 άσπρες χάντρες και του ζητείται να πει «Με ποιες χάντρες φτιάχνουμε το μακρύτερο βραχιόλι, με τις καφέ ή με τις ξύλινες;». Το παιδί πρέπει να μπορεί να συνενώσει λογικά τις δυο τάξεις Α και Β για να σχηματίζει την τάξη Γ, ενώ συγχρόνως να κατανοεί ότι, αν αφαιρέσει την τάξη Β από την τάξη Γ, θα λάβει την τάξη Α, καθώς επίσης και το όμοιο ότι, αν αφαιρέσει την τάξη Α από την τάξη Γ, θα λάβει την τάξη Β. Δηλαδή ότι ισχύουν συγχρόνως οι πράξεις : Α+Β=Γ, Γ-Α=Β και Γ-Β=Α. (Εξελικτική ψυχολογία, Παρασκευοπούλου Ι., τόμος 3,4, σελ 44)

Σύμφωνα με τον κανόνα της αντιστάθμισης (compensation), για κάθε νοητική πράξη που εκμηδενίζει ή ισοσταθμίζει το αποτέλεσμα της πρώτης. Έτσι, το αποτέλεσμα του πολλαπλασιασμού 2×3 για να μας δώσει 6, μπορεί να αντισταθμιστεί με τη διαίρεση 6:3 για να μας δώσει 3. Ο κανόνας αυτός είναι εμφανής σε προβλήματα διατήρησης ενός χαρακτηριστικού (ποσότητας, βάρους, όγκου κ.ά.). Αυτό αποδεικνύεται στο κλασικό πείραμα του Piaget για τη διατήρηση της ποσότητας. (Εξελικτική ψυχολογία, Παρασκευοπούλου Ι., τόμος 3,4, σελ 45)

Ένας θεμελιώδες γνώρισμα των λογικών πράξεων είναι ότι είναι οργανωμένες σε συστήματα συνόλου. Μια αληθής λογική πράξη ποτέ δεν συμβαίνει μεμονωμένα και ανεξάρτητα από άλλες, αλλά είναι μια περίπτωση σε ένα οργανωμένο σύνολο συναφών δράσεων. Τα συστήματα συνόλου που διαθέτει το παιδί της σχολικής ηλικίας περιγράφονται από τον Piaget με λογικομαθηματικά μοντέλα, τις λεγόμενες συναγωγές. (Εξελικτική ψυχολογία, Παρασκευοπούλου Ι., τόμος 3,4, σελ 45)

Πρέπει να τονιστεί ότι η αληθής πράξη προϋποθέτει τη συνύπαρξη και συλλειτουργία και των τριών παραπάνω γνωρισμάτων συγχρόνως. Αυτή η προϋπόθεση εξασφαλίζεται για πρώτη φορά περί το 7^ο έτος της ηλικίας. Σε προηγούμενες ηλικίες βεβαίως ενυπάρχουν στη νοητική συμπεριφορά του παιδιού χαρακτηριστικά της λογικής πράξης. Π.χ. ακόμη και κατά τη βρεφική ηλικία υπάρχουν γνωστικές δράσεις, μετασχηματισμοί δηλαδή δεδομένων, αλλά οι δράσεις αυτές δεν είναι ακόμη εσωτερικοποιημένες. Είναι αισθησιοκινητικές και γίνονται με την υλική διακίνηση του σώματος του παιδιού και των πραγμάτων γύρω του. (Εξελικτική ψυχολογία, Παρασκευοπούλου Ι., τόμος 3,4, σελ 45)

Εσωτερικοποίηση των δράσεων συντελείται γύρω στο 2 έτος, οπότε οι δράσεις εκτελούνται και εσωτερικώς, μέσω συμβολικής λειτουργίας. Δεν υπάρχει όμως ακόμη η δυνατότητα για αναστρεψιμότητα στη σκέψη. Το παιδί δηλαδή δεν διαθέτει ακόμη την ευελιξία της σκέψης να κινείται συγχρόνως και προς την αντίθετη κατεύθυνση, ούτε την ικανότητα να «αποκεντρώνει» την προσοχή του σε περισσότερα του ενός χαρακτηριστικά και να εκτελεί για κάθε πράξη την αντίστροφή της. Οι νοητικές πράξεις του νηπίου εξάλλου γίνονται αποσπασματικά, χωρίς συνέπεια και σταθερότητα- τις πρώιμες αυτές απόπειρες συλλογιστικής ο Piaget τις ονομάζει διαισθητικές λογικές πράξεις- και είναι μεμονωμένες γνωστικές εκδηλώσεις που δεν συνενώνονται για να δημιουργήσουν συνυπόλογα λογικά συστήματα. Για να χαρακτηριστεί μια δράση αληθής νοητική πράξη, πρέπει να είναι εσωτερικευμένη στη σκέψη, αναστρέψιμη και οργανωμένη σε ευρύτερες ομάδες συνόλου. (Εξελικτική ψυχολογία, Παρασκευοπούλου Ι., τόμος 3,4, σελ 45)

Οι συναγωγές των νοητικών πράξεων: Οι συναγωγές είναι θεωρητικά μοντέλα, λογικομαθηματικής μορφής, που διέπουν- και ερμηνεύουν- τα διάφορα νοητικά επιτεύγματα του παιδιού της σχολικής ηλικίας. Ο Piaget έχει περιγράψει 8 διαφορετικές συναγωγές. Οι 4 αναφέρονται σε τάξεις και οι άλλες 4 σε σχέσεις. Σε κάθε ομάδα υπάρχουν δυο συναγωγές που αναφέρονται σε λογική πρόσθεση (συνένωση τάξεων ή σχέσεων) και οι δυο που αναφέρονται σε λογικό πολλαπλασιασμό (εύρεση του κοινού μέρους, της τομής, τάξεων και σχέσεων). (Εξελικτική ψυχολογία, Παρασκευοπούλου Ι., τόμος 3,4, σελ 46)

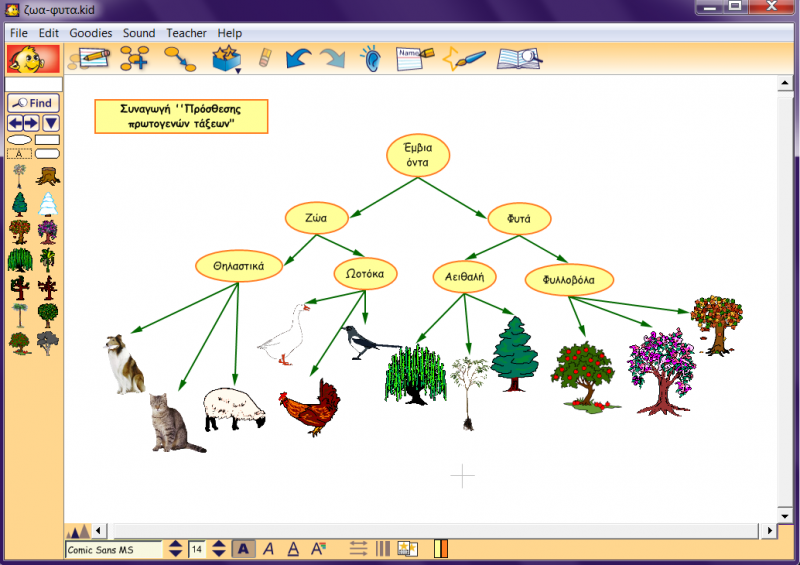
Πρόσθεση πρωτογενών τάξεων: Η συναγωγή αυτή γίνεται φανερή στην ικανότητα του παιδιού να συνενώνει πρωτογενείς- παράλληλες τάξεις και να σχηματίζει μια υπερτασσόμενη-συμπεριληπτική τάξη, δημιουργώντας έτσι ιεραρχικά συστήματα εννοιών. Π.χ. η λογική συνένωση των πρωτογενών παράλληλων τάξεων «πρόβατο», «σκύλος» και «γάτα» σχηματίζει την ανώτερου βαθμού τάξη «θηλαστικά». Ομοίως, η λογική πρόσθεση των πρωτογενών τάξεων «κότα», «χήνα» και «χελιδόνι» σχηματίζει τη συμπεριληπτική τάξη «ωοτόκα». Επίσης, η συνένωση των τάξεων «θηλαστικά» και «ωοτόκα» σχηματίζει τη συμπεριληπτική τάξη «ζώα» κ.ο.κ.. (Εξελικτική ψυχολογία, Παρασκευοπούλου Ι., τόμος 3,4, σελ.47). Σύμφωνα με τον κανόνα της αναστρεψιμότητας το παιδί μπορεί να κάνει συγχρόνως και την αντίθετη λογική πράξη, τη λογική αφαίρεση, να διασπά δηλαδή τη συμπεριληπτική τάξη και σχηματίζει πρωτογενείς τάξεις. Η αμφίδρομη αυτή λειτουργία επιτρέπει τη διατήρηση του ΟΛΟΥ και των ΜΕΡΩΝ του, (Εξελικτική ψυχολογία, Παρασκευοπούλου Ι., τόμος 3,4, σελ.47). Βεβαίως, και το παιδί της προσχολικής ηλικίας είναι σε θέση να ταξινομεί ομοειδή αντικείμενα σε τάξεις, ακόμη και να αναγνωρίζει ότι δύο ή περισσότερες τάξεις δημιουργούν μια ανώτερη τάξη. Λείπει όμως από το νήπιο η ικανότητα για μια συνολική θεώρηση του ιεραρχικού προτύπου, εφόδιο το οποίο επιτρέπει την εκτέλεση λογικών πράξεων αμφιδρομικά σε οποιοδήποτε επίπεδο της πυραμίδας με σαφή συνείδηση των μερών της, (Εξελικτική ψυχολογία, Παρασκευοπούλου Ι., τόμος 3,4, σελ.47). Τυπικό παράδειγμα πειράματος για τη διατήρηση της συναγωγής της πρόσθεσης τάξεων είναι το πείραμα του Piaget με τις «ξύλινες χάντρες διαφορετικού χρώματος» το οποίο περιγράψαμε αμέσως παραπάνω, (Εξελικτική ψυχολογία, Παρασκευοπούλου Ι., τόμος 3,4, σελ.47)

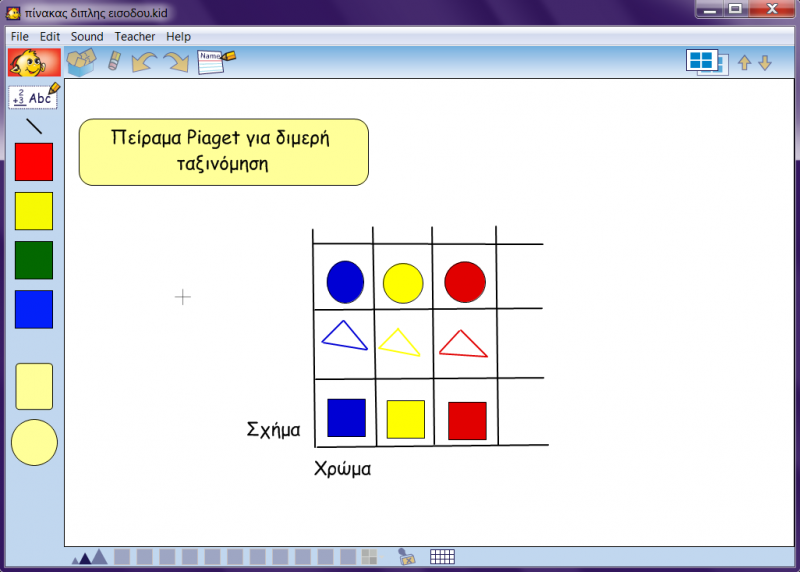
Πολλαπλασιασμός τάξεων: Το παιδί που έχει στη διάθεσή του τη συναγωγή αυτή είναι σε θέση να εντοπίζει το κοινό μέρος δύο ή περισσότερων τάξεων και να σχηματίζει τάξεις πολυμερούς ταξινόμησης. (Εξελικτική ψυχολογία, Παρασκευοπούλου Ι., τόμος 3,4, σελ.48). Τυπικό παράδειγμα πειράματος για τη διερεύνηση της συναγωγής του πολλαπλασιασμού τάξεων είναι η διμερής ταξινόμηση στοιχείων. Στο πείραμα αυτό δίνονται στο παιδί χαρτόνια διαφόρων σχημάτων (τετράγωνα, τρίγωνα, κύκλοι) και διαφόρων χρωμάτων (κόκκινα, κίτρινα, μπλε) και του ζητείται να σχηματίσει πολλαπλασιαστικές τάξεις «σχήματος και χρώματος», και να καθορίσει σε ποιο φατνίο του πίνακα πρέπει να ταξινομηθεί το κάθε χαρτόνι, (Εξελικτική ψυχολογία, Παρασκευοπούλου Ι., τόμος 3,4, σελ.48).

Πρόσθεση ασυμμετρικών σχέσεων: Οι δύο συναγωγές που περιγράψαμε αμέσως παραπάνω περιλαμβάνουν λογικές πράξεις που εκτελούνται επί τάξεων. Στη συνέχεια θα περιγράψουμε άλλες δύο συναγωγές, οι οποίες αναφέρονται σε λογικές πράξεις δύο ή περισσότερων τάξεων. (Εξελικτική ψυχολογία, Παρασκευοπούλου Ι., τόμος 3,4, σελ 49) Ο Piaget έχει μελετήσει την πορεία που ακολουθεί η απόκτηση εκ μέρους του παιδιού της έννοιας διαφόρων ειδών σχέσεων. Ας πάρουμε για παράδειγμα την ασυμμετρική σχέση (όπως Α είναι μικρότερο του Β, το Α είναι βαρύτερο του Β, το Α είναι ταχύτερο του Β), της οποίας τα στοιχεία έχουν σύνδεση μεταβατική. Ο όρος μεταβατικότητα (transitivity) δηλώνει ότι αν το Α είναι μικρότερο του Β (Α<Β) και το Β μικρότερο του Γ (Β<Γ), τότε κατά λογική αναγκαιότητα και το Α είναι μικρότερο του Γ (Α<Γ). Το παιδί της σχολικής ηλικίας, έχοντας ενώπιων του πρώτα το ζεύγος των βώλων Α και Β και στη συνέχεια το ζεύγος των βώλων Β και Γ, μπορεί να κάνει δύο συγκρίσεις: «Ο βώλος Α είναι μικρότερος από το βώλο Β και ο βώλος Β είναι μικρότερος από το βώλο Γ» και να μας βεβαιώσει ότι «και ο βώλος Α είναι μικρότερος από το βώλο Γ», χωρίς να κάνει απευθείας σύγκριση των βώλων Α και Γ, γιατί διαβλέπει την Τρίτη αυτή σχέση ως λογική συνέπεια των δύο πρώτων σχέσεων. Το παιδί της προσχολικής ηλικίας δεν μπορεί να παραγάγει λογικώς την τρίτη σχέση χωρίς εμπειρική διαπίστωση, χωρίς την απευθείας σύγκριση των δύο μεγεθών. Το παιδί της σχολικής ηλικίας λύνει προβλήματα πρόσθεσης ασυμμετρικών σχέσεων –το είδος των προβλημάτων αυτών λέγεται σειροθέτηση- γιατί κατανοεί ότι κάθε στοιχείο της σειράς πρέπει να εξετάζεται κάτω από τη διπλή σχέση: ότι είναι συγχρόνως μικρότερο από το επόμενο του και μεγαλύτερο από το προηγούμενο του (Α<Β και συγχρόνως Β<Γ). (Εξελικτική ψυχολογία, Παρασκευοπούλου Ι., τόμος 3,4, σελ 49)

Πολλαπλασιασμός ασύμμετρων σχέσεων: Στη παρούσα συναγωγή, αντί τάξεων, περιέχονται ασυμμετρικές σχέσεις. Το παιδί που έχει στη διάθεσή του τη συναγωγή αυτή είναι σε θέση να σχηματίζει σχέσεις πολυμερούς ταξινόμησης. (Εξελικτική ψυχολογία, Παρασκευοπούλου Ι., τόμος 3,4, σελ 50). Τυπικό παράδειγμα διερεύνησης της συναγωγής του πολλαπλασιασμού σχέσεων είναι το εξής πείραμα του Piaget: Δίνονται στο παιδί κούκλες διαφόρων μεγεθών και ισάριθμα κουτιά διαφορετικού μεγέθους και του ζητείται να διαρρυθμίσει τις κούκλες και τα κουτιά κατά τρόπο ώστε κάθε κούκλα να αντιστοιχεί στο κουτί της. Το παιδί της σχολικής ηλικίας γνωρίζει ότι, αν διαρρυθμίσει τις κούκλες σε μια σειρά με αυξανόμενο μέγεθος και στη συνέχεια τα κουτιά σε μια άλλη σειρά με αυξανόμενο μέγεθος, θα έχει επιτύχει την επιθυμητή αντιστοιχία. (Εξελικτική ψυχολογία, Παρασκευοπούλου Ι., τόμος 3,4, σελ 50,51).

Πείραμα του Piaget για: τον πολλαπλασιασμό ασυμμετρικών σχέσεων (αντιστοίχιση)

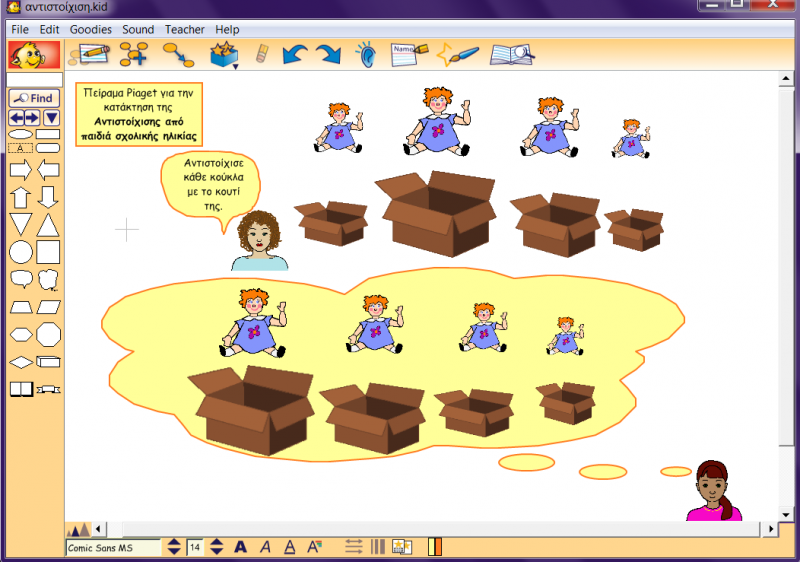
Γνωστικά επιτεύγματα του παιδιού της σχολικής ηλικίας: Είναι φανερό ότι το παιδί της σχολικής ηλικίας έχει να επιδείξει στο νοητικό τομέα θεμελιώδεις προόδους, έναντι των προηγουμένων ηλικιών, με κορυφαία κατάκτηση την ικανότητα να χρησιμοποιεί αληθείς νοητικές λογικές πράξεις κατά τρόπο σταθερό και συνεπή. Τα νέα αυτά γνωστικά εφόδια κάνουν φανερή την παρουσία τους στον ιδιαίτερο τρόπο με τον οποίο το παιδί της ηλικίας αυτής λύνει ορισμένα χαρακτηριστικά γνωστικά προβλήματα.

Στη συνέχεια θα περιγράψουμε τον τρόπο με τον οποίο το παιδί της σχολικής ηλικίας λύνει τέσσερα είδη γνωστικών προβλημάτων: 1) την ταξινόμηση, 2) τη σειροθέτηση, 3) τη διατήρηση και 4) την αρίθμηση. (Εξελικτική ψυχολογία, Παρασκευοπούλου Ι., τόμος 3,4, σελ 52)

1)Ταξινόμηση: Ως την ηλικία των 7 ετών το παιδί έχει μια στοιχειώδη ικανότητα για κατηγοριοποίηση. Δεν έχει όμως αναπτύξει πλήρως την ικανότητα για να διακρίνει τα κυρίαρχα χαρακτηριστικά που διαφοροποιούν τα μέλη μιας ομάδας από τα μέλη μιας άλλης ομάδας, ούτε είναι σε θέση να κατασκευάσει πλήρη ιεραρχικά συστήματα με επάλληλες, παράλληλες και υπάλληλες τάξεις.(Εξελικτική ψυχολογία, Παρασκευοπούλου Ι., τόμος 3,4, σελ 52). Ειδικότερα στο προεννοιολογικό στάδιο (3^ο και 4^ο έτος), το παιδί ομαδοποιεί τα αντικείμενα που του δίνονται με βάση κυρίως τις άμεσες αντιληπτικές του εμπειρίες (μορφολογικά συναθροίσματα, μερική κατηγοριοποίηση), χωρίς όμως να μπορεί να σχηματίζει πραγματικές τάξεις-κατηγορίες. Η αδυναμία αυτή οφείλεται στο ότι το νήπιο δεν μπορεί να διακρίνει ακόμη τα κύρια γνωρίσματα που καθορίζουν τα όρια μιας τάξης. Στο διαισθητικό στάδιο (5^ο και 6^ο έτος), το παιδί ομαδοποιεί τα αντικείμενα σε σύνολα που μοιάζουν με λογικές τάξεις. Παρουσιάζει δηλαδή για πρώτη φορά μια κάποια ικανότητα για ιεράρχηση των τάξεων. Οι κατηγοριοποιήσεις όμως αυτές γίνονται κατά τρόπο διαισθητικό-ενορατικό, χωρίς το παιδί σαφώς να κατανοεί τις σχέσεις ανάμεσα στα επίπεδα της ιεραρχικής ταξινόμησης και να τις εφαρμόζει στις κατηγοριοποιήσεις του με συνέπεια και σταθερότητα, (Εξελικτική ψυχολογία, Παρασκευοπούλου Ι., τόμος 3,4, σελ 52). Το παιδί της σχολικής ηλικίας, των συγκεκριμένων νοητικών πράξεων, ξεπερνά τους περιορισμούς της προσχολικής ηλικίας: μπορεί να σχηματίζει λογικές τάξεις, τις οποίες μπορεί να εντάσσει σε ευρύτερα ιεραρχικά συστήματα. Το παιδί από το 7^ο έτος ακόμη έτος μπορεί να απομονώνει κάθε φορά ένα ή περισσότερα διαφορετικά χαρακτηριστικά των αντικειμένων και να σχηματίζει τάξεις με σαφή όρια. Συγχρόνως όμως, ενώ ταξινομεί ένα αντικείμενο σε μια ορισμένη τάξη, δεν παύει να γνωρίζει ότι το αντικείμενο αυτό μπορεί να ταξινομηθεί παράλληλα, κα σε μια δεύτερη, μια τρίτη…… τάξη. Επίσης, μπορεί να συνενώνει διάφορες παράλληλες τάξεις για να σχηματίσει μια υποκείμενη τάξη. Συγχρόνως όμως, ενώ σχηματίζει την υποκείμενη αυτή τάξη -το ΟΛΟ-, δεν παύει να γνωρίζει ότι παράλληλα μπορεί να σχηματίζει, από τη συμπεριληπτική αυτή τάξη, τις επιμέρους πρωτογενείς τάξεις- τα ΜΕΡΗ. (Εξελικτική ψυχολογία, Παρασκευοπούλου Ι., τόμος 3,4, σελ 52-53). Τυπικό παράδειγμα πειράματος για τη διερεύνηση του γνωστικού σχήματος της ιεραρχικής οργάνωσης τάξεων είναι το εξής πείραμα του Piaget: Ο ερευνητής παρουσίαζε στα παιδιά εικόνες με λουλούδια και με άλλα αντικείμενα. Το παιδί έπρεπε «να βάλει μαζί σε ομάδες όλα τα πράγματα που είναι παρόμοια». Από την ηλικία των 7 ετών το παιδί αρχίζει όχι μόνο να ομαδοποιεί χωριστά τις εικόνες με λουλούδια από τις εικόνες χωρίς λουλούδια, αλλά και να δημιουργεί υποκατηγορίες –υπάλληλες τάξεις- σε ένα πλήρες ιεραρχικό σύστημα και να κατανοεί τις σχέσεις μεταξύ των διαφόρων βαθμίδων στην ταξινόμηση. Έτσι, μπορεί με βεβαιότητα να δηλώσει π.χ. ότι τα λουλούδια είναι περισσότερα από τα τριαντάφυλλα ή ότι αν από τα λουλούδια βγάλουμε τα τριαντάφυλλα, θα μας μείνουν τα γαρίφαλα ή ότι τα κίτρινα τριαντάφυλλα είναι λιγότερα από τα τριαντάφυλλα και από τα λουλούδια κ.τ.ό. Αντίθετα, το παιδί της προσχολικής ηλικίας αδυνατεί να απαντήσει σωστά τις ερωτήσεις αυτές, γιατί η σκέψη του δεν είναι ακόμη αναστρέψιμη και δεν διατηρεί συγχρόνως το ΟΛΟ και τα ΜΕΡΗ του. (Εξελικτική ψυχολογία, Παρασκευοπούλου Ι., τόμος 3,4, σελ 53).

2)Σειροθέτηση: Το πρόβλημα της σειροθέτησης συνίσταται στη τοποθέτηση αντικειμένων σε λογική σειρά που αναπαριστά σχέσεις ανισότητας μεταξύ αυτών των αντικειμένων, όπως: Α>Β>Γ>Δ… ή Α<Β<Γ<Δ… Βασική προϋπόθεση για επιτυχή σειροθέτηση είναι η ικανότητα να αναπαριστά εσωτερικώς την όλη σειρά όπως αναμένεται να διαμορφωθεί όταν σειροθετηθούν όλα τα αντικείμενα, καθώς επίσης και η ικανότητα να κατανοεί ότι κάθε στοιχείο της ακολουθίας βρίσκεται συγχρόνως σε σχέση «ανωτερότητας» προς το αμέσως προηγούμενό του στοιχείο και σε σχέση «κατωτερότητας» προς το αμέσως επόμενό του στοιχείο. (Εξελικτική ψυχολογία, Παρασκευοπούλου Ι., τόμος 3,4, σελ 54). Ο Piaget διακρίνει δύο είδη σειροθετήσεων: την απλή σειροθέτηση, όπου η διευθέτηση των διαφορών γίνεται σε ανιούσα ή κατιούσα σειρά ως προς μία μόνο διάσταση και την πολλαπλή σειροθέτηση, όπου η διευθέτηση των διαφορών, σε ανιούσα ή κατιούσα σειρά, γίνεται ως προς δύο διαστάσεις συγχρόνως. Παράδειγμα προβλήματος απλής σειροθέτησης είναι όταν δίνουμε στο παιδί μερικά όμοια ξυλάκια διαφορετικού μήκους και του ζητάμε να τα διευθετήσει στην «κανονική» τους θέση, από το μικρότερο ως το μεγαλύτερο (ή το αντίστροφο), ή, όταν του δίνουμε μερικούς όμοιους κύβους διαφόρων μεγεθών και του ζητάμε να φτιάξει έναν «κανονικό» πύργο, ή, όταν του δίνουμε όμοια κύπελλα διαφορετικού διαμετρήματος και του ζητάνε να τα βάλει το ένα μέσα στο άλλο και όλα να χωρέσουν στο μεγαλύτερο κύπελλο. Παράδειγμα πολλαπλής σειροθέτησης είναι όταν δίνουμε στο παιδί μερικές όμοιες κούκλες διαφορετικών μεγεθών και ισάριθμα όμοια κουτιά διαφορετικού ύψους και του ζητάμε να βάλει την κάθε κούκλα μέσα στο κουτί της. (Εξελικτική ψυχολογία, Παρασκευοπούλου Ι., τόμος 3,4, σελ 54). Η ικανότητα της σειροθέτησης, τόσο απλής όσο και πολλαπλής, κατακτάται, όπως η ικανότητα της ταξινόμησης, σε τρία στάδια. Στο πρώτο στάδιο- το προεννοιολογικό (3 και 4 ετών)- δεν υπάρχει εσωτερική αναπαράσταση της τελικής μορφής που αναμένεται να πάρει η σειρά των αντικειμένων. Η σειροθέτηση στο στάδιο αυτό συνίσταται σε μια ασυντόνιστη και ασυστηματοποίητη τοποθέτηση των αντικειμένων σε ακολουθίες των 2-3 αντικειμένων, με συχνή παρεμβολή και μεμονωμένων αδιάτακτων στοιχείων. Το νήπιο δεν διαθέτει ακόμη την ορθόδοξη μέθοδο της σειροθέτησης, δηλαδή πρώτα να επιλέξει, από όλα τα αντικείμενα, το μικρότερο (ή το μεγαλύτερο). Ενσυνεχεία, από τα υπόλοιπα στοιχεία να επιλέξει πάλι το μικρότερο (ή το μεγαλύτερο) και να το τοποθετήσει δίπλα στο πρώτο. Κατόπιν, να επιλέξει πάλι το μικρότερο (ή το μεγαλύτερο) από τα υπόλοιπα και να το τοποθετήσει δίπλα στο δεύτερο στοιχείο κ.ο.κ. Η διαδικασία αυτή της επιλογής του μικρότερου (ή του μεγαλύτερου) από τα αντικείμενα που κάθε φορά απομένουν και της τοποθέτησής του στην επόμενη θέση συνεχίζεται ωσότου εξαντληθούν όλα τα αντικείμενα. (Εξελικτική ψυχολογία, Παρασκευοπούλου Ι., τόμος 3,4, σελ 55).

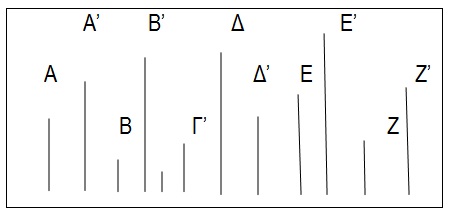
Στο δεύτερο στάδιο -διαισθητικό (5 και 6 ετών)- υπάρχει κάποια εσωτερική αναπαράσταση της αναμενόμενης τελικής ακολουθίας. Τα αντικείμενα σειροθετούνται επιτυχώς μερικές φορές, αλλά το παιδί καταλήγει στο σωστό αυτό αποτέλεσμα μετά από πολλές δοκιμές και αποτυχίες. Η έλλειψη σαφούς εσωτερικής αναπαράστασης της όλης σειράς γίνεται φανερή αν, σε μια σειρά που μόλις το παιδί της ηλικίας αυτή κατασκεύασε σωστά, παρεμβάλουμε αντικανονικά ένα στοιχείο, το παιδί συναντά δυσκολία να αποκαταστήσει την κανονικότητα της σειράς. Αντί να εντοπίσει την προσοχή του μόνο στο αδιάτακτο στοιχείο και να το τοποθετήσει στην κατάλληλη θέση, καταστρέφει ολόκληρη τη σειρά και προσπαθεί να την ανασυνθέσει εξαρχής. Στο τρίτο στάδιο -της συγκεκριμένης σκέψης (7 ως 11 έτος)- το παιδί, κατέχοντας τις λογικές πράξεις και συναγωγές τους, μπορεί πλέον σταθερά να προβαίνει σε επιτυχείς σειροθετήσεις, χωρίς δοκιμές και αποτυχίες. Στη σκέψη του παιδιού της ηλικίας αυτής υπάρχει σαφής αναπαράσταση της αναμενόμενης τελικής μορφής της ακολουθίας και η έννοια της μεταβατικότητας των διαφορών. (Εξελικτική ψυχολογία, Παρασκευοπούλου Ι., τόμος 3,4, σελ 55-56). Η πολλαπλή σειροθέτηση, σε σύγκριση προς την απλή, προϋποθέτει πολυπλοκότερη διαδικασία. Κατά την προσχολική ηλικία δεν είναι δυνατή η πολλαπλή ταξινόμηση ή σειροθέτηση, γιατί το νήπιο δεν μπορεί να συνεξετάσει περισσότερα του ενός χαρακτηριστικά τη φορά. Η δυνατότητα πολλαπλής σειροθέτησης αρχίζει να εμφανίζεται μετά το 7 έτος, όταν πλέον η αντίληψη του παιδιού αποκεντρώνεται. Στην ηλικία αυτή το παιδί μπορεί να συνεξετάσει περισσότερα του ενός χαρακτηριστικά συγχρόνως. Κατέχει δηλαδή το γνωστικό σχήμα της συναγωγής του πολλαπλασιασμού ασυμμετρικών τάξεων. (Εξελικτική ψυχολογία, Παρασκευοπούλου Ι., τόμος 3,4, σελ 56).

3)Διατήρηση: Γνωστική διατήρηση σημαίνει σταθεροποίηση στη σκέψη ενός διανοητικού στοιχείου, μιας μόνιμης πνευματικής εικόνας, με την οποία γίνεται δυνατή η αναγνώριση του αναπαριστώμενου αντικειμένου, ανεξάρτητα από τις οποιεσδήποτε εξωτερικές αλλοιώσεις που υφίσταται το αντικείμενο αυτό. Η ικανότητα αυτή, η οποία είναι απαραίτητη προϋπόθεση για τη συνεπή οργάνωση του γνωσιολογικού μας συστήματος και την κατανόηση του κόσμου, δεν είναι παρούσα κατά τη γέννηση. Θα αναπτυχθεί σε επάλληλα στάδια, καθώς το παιδί προχωρεί στις διάφορες βαθμίδες οργάνωσης των διανοητικών του μηχανισμών. (Εξελικτική ψυχολογία, Παρασκευοπούλου Ι., τόμος 3,4, σελ 56). Στο χώρο της αμεταβλησίας του μεμονωμένου αντικειμένου, από το τέλος του 1ου έτους ήδη έχει εξασφαλιστεί μια γενική και αδιαφοροποίητη διατήρηση της μονιμότητας του αντικειμένου, ανεξάρτητα από τις εξωτερικές του μεταβολές. Η διατήρηση όμως αυτής έχει ένα βασικό περιορισμό: είναι περισσότερο αναγνωριστική, παραμένει δηλαδή λίγο μόνο χρόνο μετά την εξαφάνιση του αντικειμένου από το πεδίο της άμεσης αντίληψης. Περί το τέλος του 2ου έτους, με την εμφάνιση της συμβολικής λειτουργίας, η διατήρηση γίνεται και ανακλητική, αναφέρεται δηλαδή ακόμη και σε αντικείμενα που απουσιάζουν από το πεδίο της άμεσης αντίληψης επί πολύ χρόνο. Έτσι, το νήπιο από το 2ο έτος διαθέτει τη γενική έννοια του αδιαφοροποίητου μεμονωμένου αντικειμένου. (Εξελικτική ψυχολογία, Παρασκευοπούλου Ι., τόμος 3,4, σελ 56).

Στο χώρο της αμεταβλησίας των διαφόρων φυσικών μεγεθών (της ποσότητας, του βάρους, του όγκου), το παιδί της προσχολικής ηλικίας συναντά ανυπέρβλητες δυσκολίες τόσο στο στάδιο της προεννοιολογικής όσο και της διαισθητικής περιόδου, στο πείραμα με τις ποσότητες υγρού που μεταφέρουμε σε δοχεία διαφορετικού ύψους ή πλάτους και με τους βώλους πλαστελίνης που τους αλλάζουμε το σχήμα ή τους τεμαχίζουμε σε μικρότερους βώλους. Το νήπιο αρνείται ότι η ποσότητα του υγρού παραμένει η ίδια, ανεξάρτητα από το σχήμα του δοχείου που το περιέχει, ή ότι η ποσότητας πλαστελίνης παραμένει αμετάβλητη, ανεξάρτητα από το σχήμα που παίρνει. Το νήπιο, κατά την ορολογία του Piaget, δεν μπορεί να αποκεντρωθεί, να μην εστιάζει την αντίληψή του σε ένα μοναδικό στοιχείο, ώστε αν συνυπολογίζει πολλές διαστάσεις συγχρόνως και να εξετάζει την αλληλεπίδρασή τους. Στηρίζεται σε μια μονομερή αντιληπτική άποψη (το μήκος, το πλάτος, το ύψος ή το πλήθος), χωρίς να συνυπολογίζει ταυτόχρονα τον αντισταθμιστικό ρόλο άλλων αλλαγών (αλλαγές στο ύψος του δοχείου αντισταθμίζονται από αντίστοιχες αλλαγές στο πλάτος του, αλλαγές στο μήκος του κυλίνδρου εξισορροπούνται από αλλαγές στην ακτίνα του, ή αλλαγές στο πλήθος αντισταθμίζονται σε αντίστοιχες αλλαγές στο μέγεθος). (Εξελικτική ψυχολογία, Παρασκευοπούλου Ι., τόμος 3,4, σελ 57). Αντίθετα το παιδί σχολικής ηλικίας, που έχει στη διάθεσή του το λογικό κανόνα της αντιστρεψιμότητας, κατανοεί για πρώτη φορά την έννοια της αντιστάθμισης, ότι δηλαδή αλλαγές στο ύψος του υγρού αντισταθμίζονται από αλλαγές στο πλάτος, με αποτέλεσμα η ποσότητα να παραμένει η ίδια. Η στρατηγική του παιδιού έχει επίσης αλλάξει: παύει να εστιάζει τώρα την προσοχή του μόνο στο ύψος ή μόνο στο πλάτος κάθε φορά, αλλά συνεκτιμά και τις δυο διαστάσεις συγχρόνως. Επιπλέον, έχει την ικανότητα να παρακολουθεί και να κατανοεί τις διαδοχικές φάσεις μετασχηματισμού της μορφής του υγρού, από τις όμοιες (με το ίδιο πλάτος και ύψος) φιάλες, στις φιάλες με διαφορετικές διαστάσεις, μια ικανότητα που δεν είχε στην νηπιακή ηλικία. (Εξελικτική ψυχολογία, Παρασκευοπούλου Ι., τόμος 3,4, σελ 57). Πρέπει να τονιστεί ότι η ικανότητα για γνωστική διατήρηση δεν κατακτάται ταυτόχρονα για όλες τις ιδιότητες των φυσικών αντικειμένων, αλλά σε διαφορετικές χρονικές περιόδους από το 7ο ως το 11ο έτος. Πρώτη κατακτάται η διατήρηση της ποσότητας (και η συναφής προς την κατάκτηση αυτή έννοια του αριθμού) στο 7ο ή 8ο έτος, κατόπιν η διατήρηση του βάρους στο 9ο έτος και τελευταία η διατήρηση του όγκου στο 11ο έτος. Το φαινόμενο αυτό, ότι δηλαδή η κατάκτηση της έννοιας της γνωστικής αμεταβλησίας δεν γίνεται συγχρόνως για όλες τις ιδιότητες των φυσικών αντικειμένων, αλλά κλιμακώνεται μέσα στα όρια της ίδιας περιόδου νοητικής ανάπτυξης, λέγεται οριζόντια κλιμάκωση της ανάπτυξης. (Εξελικτική ψυχολογία, Παρασκευοπούλου Ι., τόμος 3,4, σελ 57).

4)Αρίθμηση: Ο Piaget υποστηρίζει ότι η εξέλιξη της έννοιας του αριθμού οικοδομείται σε συνάφεια με την κατάκτηση της ικανότητας για ταξινόμηση, για σειροθέτηση και για διατήρηση της ποσότητας. (Εξελικτική ψυχολογία, Παρασκευοπούλου Ι., τόμος 3,4, σελ 58). Αναφορικά με την έννοια του αριθμού και την έννοια της ταξινόμησης και της σειροθέτησης, πρέπει να λεχθεί ότι κάθε στοιχείο του αριθμητικού συστήματος υποδηλώνει συγχρόνως μια τάξη-κατηγορία ομοειδών μονάδων και μια θέση σε κάποια σειρά. Ο αριθμός 5 π.χ. υποδηλώνει την τάξη των πέντε ομοειδών μονάδων και συγχρόνως την Πέμπτη θέση στη σειρά 1,2,3,4,5,6….. Η τάξη που υποδηλώνει κάθε αριθμός σχετίζεται με την ποσοτική ή την απόλυτη σημασία του αριθμού (μια, δύο, τρεις, τέσσερις, πέντε…. μονάδες), ενώ η θέση σχετίζεται με την τακτική σημασία του αριθμού (πρώτος, δεύτερος, τρίτος, τέταρτος, πέμπτος,…… στη σειρά). Η απόκτηση λοιπόν της έννοιας του αριθμού προϋποθέτει την κατανόηση τόσο της απόλυτης όσο και της τακτικής σημασίας του αριθμού. Το παιδί λοιπόν κατέχει την έννοια του αριθμού π.χ. 8, όταν μας δώσει αποδείξεις ότι έχει κατανοήσει τη διττή σημασία του αριθμού 8, ότι δηλαδή πρόκειται για ένα σύνολο 8 ομοειδών μανάδων (8 μολυβιών, 8 βιβλίων…….) και συγχρόνως ότι το σύνολο αυτό των 8 μονάδων είναι μεγαλύτερο του συνόλου των 7 μονάδων και μικρότερο του συνόλου των 9 μονάδων. (Εξελικτική ψυχολογία, Παρασκευοπούλου Ι., τόμος 3,4, σελ 58).

Τίθεται λοιπόν το ερώτημα: σε ποια ηλικία αποκτά το παιδί την αληθινή έννοια του αριθμού; Ποια είναι η εξελικτική πορεία που ακολουθεί η κατάκτηση της έννοιας του αριθμού; Είναι γεγονός ότι από τα πρώτα χρόνια της νηπιακής ηλικίας τα παιδιά μπορούν να μετρούν άνετα, ανεβαίνοντας και κατεβαίνοντας την αριθμητική κλίμακα σωστά. Τέτοιου είδους προφορικές αριθμήσεις τις κάνουν τα νήπια είτε ως είδος απαγγελίας (απλώς απαγγέλουν τα ονόματα των αριθμών στη σωστή σειρά, χωρίς να έχουν μπροστά τους συγκεκριμένα αντικείμενα τα οποία να καταμετρούν) είτε σε συνάρτηση με την καταμέτρηση αντικειμένων, όπου σαφώς προσπαθούν, αξιοποιώντας κυρίως τοποχωρικά στοιχεία, να μην παραλείψουν κανένα αντικείμενο και κάθε αντικείμενο να το μετρούν μόνο μια φορά. Επίσης, είναι γνωστό ότι το παιδί της προσχολικής ηλικίας μπορεί να εκτιμήσει σωστά αριθμητικές ποσότητες όταν αυτές είναι μικρές (3 ξυλάκια, 4 κουμπιά) με μια συνολική ματιά, χωρίς να μετρήσει ένα-ένα τα αντικείμενα. Οι πρώιμες αυτές αριθμητικές κατακτήσεις των παιδιών, όσο και αν εντυπωσιάζουν και χαροποιούν τους γονείς, επουδενί δείχνουν ότι το παιδί έχει κατακτήσει την αληθή έννοια του αριθμού. (Εξελικτική ψυχολογία, Παρασκευοπούλου Ι., τόμος 3,4, σελ 58).

Την εξελικτική πορεία που ακολουθεί η απόκτηση και η συνοργάνωση της έννοιας της διατήρησης της ποσότητας και της έννοιας του αριθμού την έχει μελετήσει ο Piaget με διάφορα πειράματα αντιστοιχίας ποσοτήτων και ισοδυναμίας συνόλων. Τυπικό παράδειγμα τέτοιου πειράματος είναι το πείραμα του Piaget που ακολουθεί: Παρουσιάζουμε στο παιδί μια σειρά από αυγοθήκες, σε ίση απόσταση η μια αυγοθήκη από την άλλη, και μια ισάριθμη σειρά αυγά διευθετημένα σε ένα προς ένα αντιστοιχία με τις αυγοθήκες. Το παιδί αναγνωρίζει ότι υπάρχει ποσοτική- αριθμητική ισότητα μεταξύ των δύο σειρών. Κατόπιν, αφήνουμε τις αυγοθήκες στη θέση τους και αραιώνουμε τα αυγά. Το παιδί του προεννοιολογικού σταδίου (3^ο και 4^ο έτος) θα δηλώσει ότι τα αυγά τώρα είναι περισσότερα από ότι οι αυγοθήκες, γιατί τα αυγά καταλαμβάνουν μεγαλύτερο συνολικό μήκος. Ακόμη και αν τα αυγά είναι λιγότερα, το παιδί της ηλικίας αυτής επιμένει ότι τα αραιωμένα αυγά είναι περισσότερα από ότι οι συμπτυγμένες αυγοθήκες, στηριζόμενο αποκλειστικά και μόνο στη διαφορά μήκους των σειρών. Στην ηλικία αυτή το παιδί ταυτίζει το χώρο που καταλαμβάνει η σειρά με το αριθμητικό της μέγεθος, χωρίς να συνυπολογίζει την πυκνότητα της σειράς. (Εξελικτική ψυχολογία, Παρασκευοπούλου Ι., τόμος 3,4, σελ 58-59). Συναφές με το παραπάνω πείραμα, αποτελεί το πείραμα του Piaget με τα κρεβάτια και τις κούκλες για τη διατήρηση του αριθμού και την αντιστοίχιση. (Piagetian tests for the primary school, K.R. Fogelman, σελ 50).

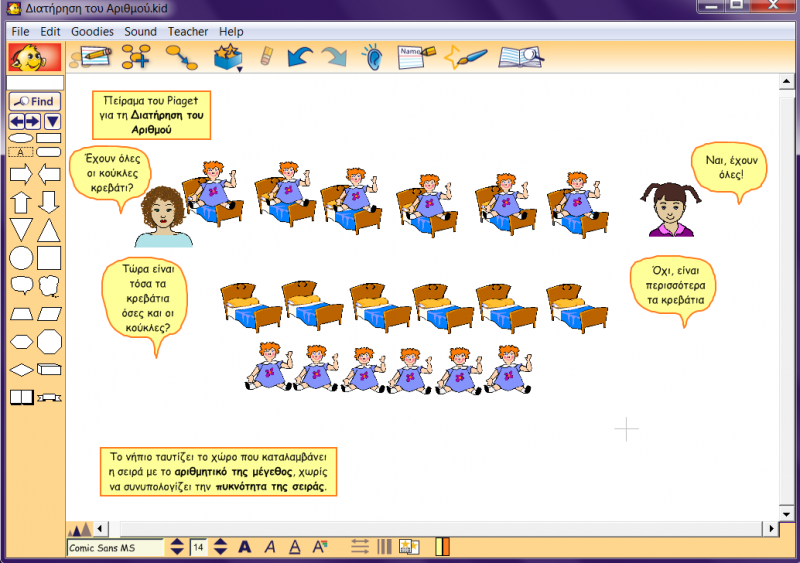
Ας εξετάσουμε ακόμη ένα συναφές πείραμα: Παρουσιάζουμε στο παιδί ζεύγη σειρών από χάντρες διαφορετικού μήκους, όπως στο σχ. 12. Το παιδί καλείται να κρίνει ποια από τις δύο σειρές έχει κάθε φορά τις περισσότερες χάντρες. Όπως μπορεί κανείς να διακρίνει, υπάρχουν δύο στοιχεία που παρέχουν πληροφορίες για το αριθμητικό μέγεθος του ζεύγους των παράλληλων σειρών: το μήκος και η πυκνότητα. Αν οι δύο σειρές είναι του ίδιου μήκους, αλλά η μία είναι πυκνότερη της άλλης, η πυκνότερη σειρά είναι πολυπληθέστερη. Αν η μια σειρά είναι μικρότερη σε μήκος και πυκνότερη και οι διαφορές μήκους-πυκνότητας εξισορροπούνται αμοιβαία, τότε οι δύο σειρές έχουν τον ίδιο αριθμό χαντρών. Αν, τέλος, η μια σειρά είναι μακρύτερη και πυκνότερη, η σειρά αυτή είναι και η πολυπληθέστερη. Οι απαντήσεις των παιδιών απηχούν και το εξελικτικό στάδιο το οποίο διέρχονται, ανάλογα με την ηλικία τους:

Α) Στις ηλικίες ως το 4^ο έτος, οι απαντήσεις του παιδιού υπαγορεύονται απόλυτα από το σχετικό μήκος των σειρών. Έτσι, στο σχ.12 για το ζεύγος Α το παιδί επιμένει ότι και οι δύο σειρές έχουν ίσο αριθμό χαντρών, γιατί και οι δυο σειρές έχουν το ίδιο μήκος. Το ίδιο ισχυρίζεται και για το ζεύγος Β. Για τα υπόλοιπα ζεύγη επιμένει ότι η μακρύτερη σειρά είναι και η πολυπληθέστερη ( στο ζεύγος Γ η 2^η σειρά, στο ζεύγος Δ η 1^η σειρά, στο ζεύγος Ε η 2^η σειρά και στο ζεύγος Ζ η 1^η σειρά)

Β) Στις ηλικίες 5^ο και 6^ο έτος, το παιδί αρχίζει να μη βασίζει την εκτίμησή του, σε όλες τις περιπτώσεις, αποκλειστικά στο μήκος της σειράς, αλλά να λαμβάνει υπόψη του και την πυκνότητα της σειράς. Συχνά δηλώνει, όπως και στις μικρότερες ηλικίες, ότι η μακρύτερη σειρά είναι η πολυπληθέστερη, αλλά μερικές φορές αντιλαμβάνεται επίσης ότι η μικρότερη σειρά είναι η πολυπληθέστερη, γιατί οι χάντρες της είναι πιο κοντά η μια στην άλλη. Η αυξανόμενη σημασία της πυκνότητας για τις απαντήσεις του παιδιού καταφαίνεται και από τη σύγκριση των απαντήσεων που δίνει σχετικά με τα έξι ζεύγη

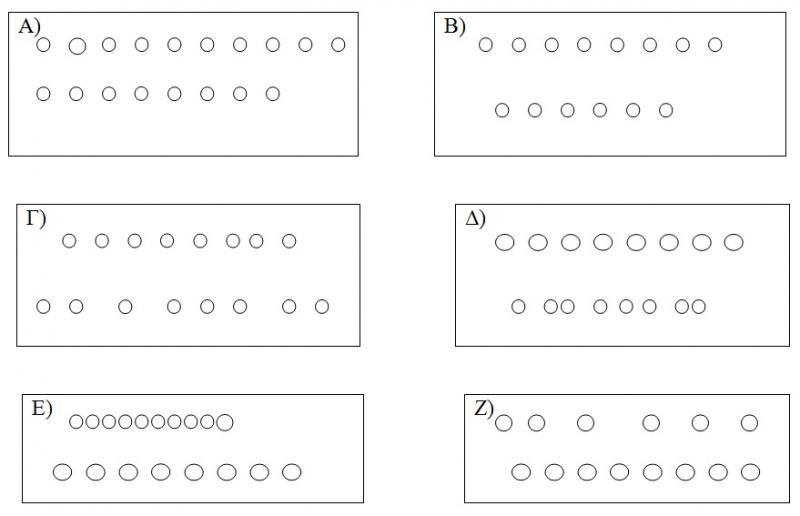
σειρών του σχ. 12. Έτσι, στα ζεύγη Γ, Δ, Ε και Ζ, οι μακρύτερες σειρές θεωρούνται ως πολυπληθέστερες. Αντίθετα, στα ζεύγη Α και Β, όπου οι δυο σειρές είναι ισομήκεις, οι απαντήσεις του παιδιού καθορίζονται από τη σχετική πυκνότητα κάθε σειράς : πολυπληθέστερες θεωρούνται – και είναι- και στα δυο ζεύγη η 1^η σειρά. Η πρόοδος που έχει κάνει το παιδί στο στάδιο αυτό είναι σαφής. Υπάρχει όμως ακόμα μια βασική αδυναμία: το παιδί δεν έχει την ικανότητα να λαμβάνει υπόψη του το μήκος και την πυκνότητα συγχρόνως. Γι’ αυτό οι απαντήσεις του είναι σωστές, όταν εξαρτώνται μόνο από το μήκος ή μόνο από την πυκνότητα. Συνήθως όμως είναι λανθασμένες, όταν απαιτείται συνεξέταση και συγκερασμός των δυο διαστάσεων. Αυτός ο περιορισμός αίρεται μετά το 7^ο έτος.

Γ) Από το 7^ο έτος της ηλικίας, το παιδί αρχίζει να κρίνει ότι η αρχική αριθμητική σχέση μεταξύ δυο ομάδων αντικειμένων (ίσων ή άνισων) διατηρείται, έστω και αν μεταβάλλεται το μήκος ή η πυκνότητά τους. Η κρίση του αυτή έχει ως αφετηρία το νέο γνωστικό σχήμα ότι κάθε αλλαγή στο μήκος συνεπάγεται και ανάλογη αλλαγή στην πυκνότητα, ότι δηλαδή η σειρά που επιμηκύνεται γίνεται συγχρόνως και αραιότερη. Με άλλα λόγια, στο στάδιο αυτό έχουμε πλήρη λειτουργία του κανόνα της αντιστάθμισης. (Εξελικτική ψυχολογία, Παρασκευοπούλου Ι., τόμος 3,4, σελ 60-61)

Η παράλληλη εξέλιξη της έννοιας του αριθμού και της έννοιας της διατήρησης της ποσότητας, όπως διαγράφεται στη θεωρία του Piaget, έχει επιβεβαιωθεί και από σχετικές διαπολιτιστικές έρευνες. Σε μια έρευνα που έγινε με παιδιά προσχολικής και σχολικής ηλικίας στη χώρα μας εξετάστηκε η εξέλιξη της έννοιας του αριθμού με πειράματα διατήρησης της ύλης και σειροθέτησης. Τα ευρήματα της έρευνας αυτής επιβεβαίωσαν την άποψη του Piaget ότι η έννοια διατήρησης της ποσότητας συμβαδίζει με την εξέλιξη της έννοιας του αριθμού. Επιβεβαιώθηκαν επίσης τα τρία στάδια που κατά τον Piaget διέρχεται το παιδί ωσότου κατακτήσει την έννοια της διατήρησης της ύλης και του αριθμού. Αξίζει να σημειωθεί ότι στην παραπάνω έρευνα διαπιστώθηκε ότι, ενώ η τυπική ηλικία για την κατάκτηση της έννοιας της διατήρησης της ποσότητας και του αριθμού είναι το 7^ο ή 8^ο έτος, υπάρχουν παιδιά (ποσοστό 12%) που κατακτούν και το τελευταίο αναπτυξιακό στάδιο των εννοιών αυτών ακόμη και από το 5^ο έτος αλλά (ποσοστό 5%) που δεν έχουν κατακτήσει το στάδιο αυτό ακόμη και μετά το 10^ο έτος της ηλικίας. (Εξελικτική ψυχολογία, Παρασκευοπούλου Ι., τόμος 3,4, σελ 61)

Από όσα είπαμε παραπάνω γίνεται φανερό ότι η κατάκτηση εκ μέρους των παιδιών της έννοιας του αριθμού διέρχεται τρία εξελικτικά στάδια:

Στο πρώτο στάδιο, ως την ηλικία 4 ετών, δεν υπάρχει αληθής έννοια του αριθμού, όπως εξάλλου δεν υπάρχει πλήρως αναπτυγμένη η ικανότητα για το σχηματισμό οποιασδήποτε έννοιας. Στην περίοδο αυτή το παιδί οδηγείται σε εσφαλμένη εκτίμηση αριθμητικών μεγεθών, γιατί είναι ακόμη δέσμιο των άμεσων αντιληπτικών δεδομένων. Αυτό που βαρύνει στην κρίση του νηπίου είναι οι διάφορες αντιληπτικές εικόνες συνόλου, στις οποίες το κυρίαρχο στοιχείο είναι συνήθως μια εξωτερική διάσταση (πχ διάταξη, μέγεθος, πυκνότητα). Παρόλα αυτά, το παιδί έχει την ικανότητα να αριθμεί –πολλές φορές μάλιστα αριθμεί σωστά ως την Τρίτη δεκάδα. Η αρίθμηση όμως αυτή είναι επιφανειακή, γιατί δεν έχει κατανοηθεί ακόμη η έννοια του απόλυτου-ακέραιου αριθμού, ότι δηλαδή μπορούμε να πάρουμε ένα νέο αριθμό, προσθέτοντας κάθε φορά μία μονάδα στον προηγούμενό του. Δεν μπορεί επίσης το παιδί να προβεί σε ποσοτικές συγκρίσεις και εκτιμήσεις. Οι συγκρίσεις και οι εκτιμήσεις του είναι ολικές, συγκριτικές επινοήσεις. Έτσι, μπορεί να εκτιμήσει σωστά μόνο μικρές ποσότητες -2 ως 3 αντικείμενα- χωρίς ακόμη να μπορεί να τα καταμετρήσει. (Εξελικτική ψυχολογία, Παρασκευοπούλου Ι., τόμος 3,4, σελ 61-62)

Το δεύτερο στάδιο, κατά το 5^ο και 6^ο έτος, είναι μια μεταβατική φάση, η οποία από πολλές απόψεις προαγγέλλει την πλήρη κατανόηση του αριθμού όπως την πραγματοποιούν τα μεγαλύτερα παιδιά. Η προσήλωση στα αντιληπτικά δεδομένα του προηγούμενου σταδίου αρχίζει τώρα να υποχωρεί, αλλά αυτό γίνεται ευκαιριακά και σποραδικά. Οι αντιφάσεις αυτές πάντως είναι εποικοδομητικές, από την άποψη ότι δείχνουν την αυξανόμενη ευαισθητοποίηση του παιδιού σε περισσότερες της μιας διαστάσεις του προβλήματος. Το παιδί δεν βασίζει πλέον τις εκτιμήσεις του αποκλειστικά στο μήκος πχ που καταλαμβάνει μια σειρά αντικειμένων, αλλά και στην πυκνότητα των αντικειμένων. Αρχίζει να κάνει καταμερισμό της προσοχής του σε περισσότερες της μίας όψεις του προβλήματος συγχρόνως. Ακόμη όμως δεν μπορεί να προβεί σε συνεπή συνεξέταση των διαφόρων όψεων του προβλήματος. Οι απαντήσεις του είναι σωστές μόνο στις εύκολες περιπτώσεις. Αντίθετα, στις δύσκολες περιπτώσεις (πχ οι 2 σειρές είναι άνισου μήκους, αλλά διαφέρουν ως προς την πυκνότητα) οι απαντήσεις του είναι κατά κανόνα εσφαλμένες. Ένα άλλο επίτευγμα του παιδιού των 5 και 6 ετών είναι ότι αρχίζει να αντιλαμβάνεται ότι, για να καταστήσει δυο σύνολα ίσα, πρέπει να προβεί σε προσθέσεις ή αφαιρέσεις στοιχείων. Η κατανόηση της αναγκαιότητας αυτής βεβαίως είναι ακόμα εποπτική, και όχι λογική, και δεν οδηγεί πάντοτε σε ορθά αποτελέσματα, αλλά είναι ασφαλώς μια αναμφισβήτητη πρόοδος σε σχέση προς τις προηγούμενες ηλικίες. Μπορεί λοιπόν κανείς να πει συμπερασματικά ότι το παιδί στο στάδιο αυτό έχει να επιδείξει επιτυχίες, αλλά οι επιτυχίες αυτές δεν είναι ούτε μόνιμες ούτε συστηματικές, γιατί δεν είναι ακόμη απόρροια λογικής σκέψης. (Εξελικτική ψυχολογία, Παρασκευοπούλου Ι., τόμος 3,4, σελ 62)

Στο τρίτο στάδιο, από το 7^ο και ύστερα, το παιδί εμπεδώνει πλέον και τελειοποιεί τα γνωστικά λογικά του επιτεύγματα. Η διατήρηση της ποσότητας και του αριθμού γίνεται πλέον ένα σταθερό γνωστικό σύστημα: το παιδί όχι μόνο βεβαιώνει αμέσως για την αμεταβλησία της ύλης, αλλά και δικαιολογεί τις απαντήσεις του με λογικά πλέον επιχειρήματα. Κατανοεί αντιστοιχίες μεταξύ δυο συνόλων και η γνώμη του για την ισοδυναμία δεν εξαρτάται από τις αλλαγές στη διάταξή τους στο χώρο, αλλά μόνο από προσθέσεις ή αφαιρέσεις στοιχείων. Η αντιστοιχία δηλαδή στο στάδιο αυτό ελευθερώνεται εντελώς από την εποπτική της μορφή και εκτελείται πλέον εσωτερικά σε λειτουργικό, λογικό επίπεδο. Τόσο η απόλυτη όσο και η τακτική σημασία του αριθμού γίνονται τώρα πλήρως κατανοητές. Το παιδί γνωρίζει πχ ότι το 10 μπορεί να αναφέρεται τόσο σε μια ποσότητα δέκα πραγμάτων όσο και στη δέκατη θέση σε μια σειρά. (Εξελικτική ψυχολογία, Παρασκευοπούλου Ι., τόμος 3,4, σελ 62-63)

Η κατάκτηση της έννοιας του αριθμού από το παιδί της σχολικής ηλικίας γίνεται φανερή και σε πολλούς άλλους τομείς που μπορούν να συνοψιστούν στα ακόλουθα:

Α) Το παιδί της σχολικής ηλικίας μπορεί να υπολογίσει, με μια πρώτη ματιά, το αριθμητικό μέγεθος μιας μικρής ομάδας αντικειμένων, χωρίς να καταφύγει στην αρίθμησή τους. Τέτοιες ολικές-συγκριτικές επινοήσεις μπορεί βέβαια να κάνει και το νήπιο, τώρα όμως το παιδί κατανοεί επιπλέον ότι η εκτίμηση αυτή είναι δυνατή μόνο όταν τα αντικείμενα είναι πολύ λίγα (2ή3). Όταν πρόκειται για περισσότερα αντικείμενα, γνωρίζει ότι πρέπει να τα καταμετρήσει.

Β) Η μέτρηση-αρίθμηση είναι βεβαίως ένα επίτευγμα ακόμη και προηγούμενων ηλικιών. Το νήπιο είναι σε θέση να αριθμεί σε –ή χωρίς- αντιστοιχία με αντικείμενα. Η δεξιότητα αυτή όμως δε σημαίνει ότι το νήπιο έχει κατανοήσει την έννοια του αριθμού. Στη σχολική ηλικία η μέτρηση είναι όχι μόνο ακριβής ( το παιδί κάθε αντικείμενο μία φορά χωρίς να παραλείπει κανένα) αλλά και πολυπλοκότερη. Το παιδί υποδιαιρεί ένα σύνολο σε μικρότερες ομάδες, εξάγει από μια ομάδα έναν συγκεκριμένο αριθμό αντικειμένων ή προσθέτει στην ομάδα τόσα αντικείμενα όσα του ζητηθούν. Με άλλα λόγια, μπορεί να εκτελεί αριθμητικές πράξεις με πραγματικούς χειρισμούς αντικειμένων.

Γ) Όπως ήδη αναφέραμε, το παιδί από το 7^ο έτος και ύστερα κατανοεί τις δυο βασικές διαστάσεις του αριθμού, δηλαδή την τακτική και την απόλυτη. Όταν πχ αριθμεί το 10^ο αντικείμενο σε μια ομάδα αντικειμένων, γνωρίζει ότι : 1) Το αντικείμενο αυτό είναι το 10 ο στη σειρά και 2) το σύνολο ή η ποσότητα των αντικειμένων που καταμετρήθηκαν είναι δέκα. Αντιλαμβάνεται επίσης ότι, σε μια αριθμητική σειρά, το 8 πχ είναι μια θέση υψηλότερα του 7 και μια θέση χαμηλότερα του 9

Δ) Αν δοθεί στο παιδί της σχολικής ηλικίας ένα σύνολο αντικειμένων και του ζητηθεί να κατασκευάσει ένα άλλο ισοδύναμο, το παιδί συνήθως μετράει τα αντικείμενα του πρώτου συνόλου και εν συνεχεία ξεχωρίζει άλλα τόσα –ίσο αριθμό- για το 2^ο σύνολο. Ένας άλλος τρόπος που χρησιμοποιεί το παιδί της σχολικής ηλικίας για να λύσει προβλήματα αριθμητικής ισοδυναμίας είναι να τοποθετεί τα αντικείμενα της 2^ης ομάδας ένα προς ένα, σε αντιστοιχία με τα αντικείμενα της 1^ης ομάδας. Γνωρίζει δηλαδή ότι δυο σύνολα είναι αριθμητικά ίσα, όταν υπάρχει πλήρης αντιστοιχία μεταξύ των στοιχείων τους.

Ε) Στη σχολική ηλικία το παιδί μπορεί να συγκρίνει δυο ομάδες αντικειμένων και να αποφανθεί ποια είναι μεγαλύτερη ή μικρότερη, κατανοεί δηλαδή τις σχέσεις που υποδηλώνουν οι έννοιες «περισσότερο» , «λιγότερο» ή «ίσο». Αναγνωρίζει το παιδί ότι το «περισσότερο από» ή «λιγότερο από» αναφέρεται στη σχέση ποσότητας μεταξύ των δυο συνόλων και όχι σε σύγκριση με μια τρίτη, απόλυτη ποσότητα. Η κατανόηση της ποσοτικής σχέσης μεταξύ δυο συνόλων επιτρέπει στο παιδί να προβαίνει εν συνεχεία σε αριθμητικές πράξεις που ανάλογα διατηρούν ή μεταβάλλουν αυτή τη σχέση. Συναφές είναι το ακόλουθο πείραμα του Piaget, με το οποίο προσπαθεί να διαπιστώσει την ικανότητα του παιδιού να εξισώνει δυο άνισες ποσότητες με προσθετικούς ή αφαιρετικούς συνδυασμούς: Ο ερευνητής παρουσιάζει δύο ομάδες από ξυλάκια, τη μια με 8 και την άλλα με 14, και ζητάει από το παιδί να τις κάνει ίσες. Ως την ηλικία των 5 ετών το παιδί δεν αντιλαμβάνεται τη σχέση μεταξύ των δύο συνόλων, δεν ξέρει δηλαδή ότι προσθέτοντας ξυλάκια στη μια ομάδα, τα αφαιρεί συγχρόνως από την άλλη. Στο 5^ο και 6^ο έτος το παιδί συσχετίζει τις δύο ομάδες, αλλά κατά τρόπο εμπειρικό και μετά από δοκιμές και αποτυχίες. Από το 7^ο έτος και ύστερα το παιδί είναι σε θέση πλέον να εξισώνει τις δύο ομάδες, αφαιρώντας από τη μεγαλύτερη τόσα στοιχεία όσα θα την κάνουν ίση με τη μικρότερη ομάδα (14-3=11 , 8+3 =11). Στο στάδιο αυτό δηλαδή το παιδί έχει κατακτήσει τις έννοιες της αντιστοιχίας και ισοδυναμίας δύο ομάδων, καθώς επίσης και την ικανότητα να διατηρεί ή να μεταβάλλει αυτή την ισοδυναμία με προσθέσεις και αφαιρέσεις.

Στ) Είδαμε αμέσως παραπάνω ότι το παιδί της σχολικής ηλικίας μπορεί να μεταβάλλει το σχετικό μέγεθος δυο ομάδων αντικειμένων, με προσθέσεις και αφαιρέσεις, και να κατανοεί αυτές τις μεταβολές. Είδαμε επίσης ότι το παιδί από το 7^ο έτος αρχίζει να κατακτά σταδιακά τη διατήρηση του αριθμού και της ποσότητας. Οι δυο αυτές βασικές κατακτήσεις σε συνδυασμό υποδηλώνουν την ικανότητα του παιδιού να διακρίνει τον ουσιώδη μετασχηματισμό από τον επουσιώδη, τι δηλαδή αλλοιώνει πραγματικά το αριθμητικό μέγεθος μιας ομάδας αντικειμένων. Έτσι, το παιδί της σχολικής ηλικίας αναγνωρίζει ότι η αριθμητική τιμή ενός συνόλου μεταβάλλεται, μόνο αν προστεθούν ή αφαιρεθούν στοιχεία από το σύνολο αυτό, όχι αν πχ τα στοιχεία του συμπτυχθούν ή εκταθούν στο χώρο. Τέλος, η πρόσθεση και η αφαίρεση αντιμετωπίζονται από το παιδί- όπως πραγματικά είναι- ως δυο αντίθετες πράξεις που η μια μπορεί να αναιρεί την άλλη

Ζ) Ένα τελευταίο επίτευγμα του παιδιού της σχολικής ηλικίας είναι ότι κατανοεί για πρώτη φορά τη φύση και τον τρόπο δημιουργίας των ακέραιων αριθμών. Το παιδί είναι ικανό να αναγνωρίζει το γεγονός ότι κάθε αριθμός προκύπτει πάντοτε αν στον προηγούμενό του προστεθεί μια μονάδα και ότι με τον τρόπο μια σειρά αριθμών μπορεί να επεκταθεί ωε το άπειρο με τη μορφή ασυμμετρικής σειράς. (Εξελικτική ψυχολογία, Παρασκευοπούλου Ι., τόμος 3,4, σελ 63-64).

Ικανότητες του παιδιού σχολικής ηλικίας

Από όσα είπαμε για την περίοδο των συγκεκριμένων νοητικών πράξεων γίνεται φανερό ότι το παιδί της σχολικής ηλικίας έχει πραγματοποιήσει στον τομέα της νοητικής ανάπτυξης θεμελιώδεις προόδους. Στην περίοδο των 7 ως 11 ετών για πρώτη φορά το παιδί :

Α) Παρουσιάζει αληθείς λογικές πράξεις που βασίζονται στην ικανότητα για γνωστική αντιστρεψιμότητα. Στις προηγούμενες ηλικίες οι νοητικές πράξεις γίνονται κατά τρόπο αποσπασματικό, δεν έχουν συνέπεια και σταθερότητα, είναι διαισθητικές.

Β) Ταξινομεί κατά τρόπο λογικό πρόσωπα και πράγματα. Το επίτευγμα αυτό προϋποθέτει την ικανότητα να σχηματίζει και να κατανοεί πλήρως λογικές έννοιες και τις μεταξύ τους σχέσεις.

Γ) Μπορεί να τοποθετεί σε σειρά, κατά ανιούσα ή κατιούσα κλίμακα, διάφορα μεγέθη. Μπορεί δηλαδή να σειροθετεί ασυμμετρικές σχέσεις και να εφαρμόζει στις σειροθετήσεις του αυτές το λογικό κανόνα της μεταβατικότητας.

Δ) Έχει αποκτήσει την έννοια της διατήρησης των διαφόρων φυσικών μεγεθών (ποσότητας, βάρους, όγκου). Αναγνωρίζει δηλαδή ότι ένα πράγμα είναι το ίδιο, τόσο ποιοτικά (δεν έχει αλλάξει η υφή του) όσο και ποσοτικά (δεν έχει γίνει μικρότερο ή μεγαλύτερο), παρά τις τυχόν εξωτερικές μεταβολές που έχει υποστεί.

Ε) Έχει κατακτήσει την έννοια του αριθμού τόσο ως τάξη ομοειδών πραγμάτων ( απόλυτοι αριθμοί) όσο και ως θέση μέσα στη σειρά του αριθμητικού συστήματος ( τακτικοί αριθμοί).

Στ) Εξάγει συμπεράσματα για την πραγματική κατάσταση του κόσμου που τον περιβάλλει, χωρίς να είναι απόλυτα δέσμιο των κατ’ αίσθηση αντιλήψεων.

Ζ) Έχει αποκτήσει την ικανότητα να στρέφει την προσοχή του σε περισσότερα του ενός χαρακτηριστικά κάθε φορά δηλαδή «αποκεντρώνει» την προσοχή του.

Η) Συλλαμβάνει νοητικά –και επομένως προβλέπει- όχι μόνο τις σταθερές καταστάσεις, αλλά και τις ενδιάμεσες φάσεις που παρεμβάλλονται μεταξύ της αρχικής και της τελικής φάσης. (Εξελικτική ψυχολογία, Παρασκευοπούλου Ι., τόμος 3,4, σελ 65-66)

Η νοητική όμως ανάπτυξη, παρά τις έκδηλες προόδους που έχει επιτελέσει το παιδί στις ηλικίες 7-11 έτη, δεν έχει ακόμη ολοκληρωθεί. Το παιδί της σχολικής ηλικίας υπερτερεί μεν σε σύγκριση με τον έφηβο και τον ώριμο άνθρωπο. Ο κύριος περιορισμός της σκέψης του παιδιού των 7 ως 11 ετών είναι ότι παραμένει συγκεκριμένη. Έτσι, πχ το παιδί μπορεί να λύσει σωστά το πρόβλημα της λογικής πρόσθεσης ασυμμετρικών σχέσεων με τις άνισες γραμμές, που αναφέραμε παραπάνω, μόνο όταν έχει άμεση οπτική αντίληψη του μήκους των γραμμών, όταν το υλικό της λογικής πράξης είναι συγκεκριμένο, όταν είναι απόρροια της άμεσης εμπειρίας. Αντίθετα, παρόμοιο πρόβλημα που του δημιουργεί ανυπέρβλητες δυσκολίες. (Εξελικτική ψυχολογία, Παρασκευοπούλου Ι., τόμος 3,4, σελ 66)

Η προσκόλληση του παιδιού στα φυσικά χαρακτηριστικά των ερεθισμάτων εξηγεί και ένα δεύτερο γνώρισμα-μειονέκτημα της ηλικίας αυτής. Το παιδί της σχολικής ηλικίας, στην προσπάθειά του να γνωρίσει τα πράγματα, εξετάζει τα διάφορα χαρακτηριστικά ενός ερεθίσματος ( μάζα, βάρος, μήκος, χρόνος κ.τ.ό) χωριστά το ένα από το άλλο και όχι όλα μαζί, γιατί οι γνωστικές του δυνάμεις δεν του επιτρέπουν μια συνολική, αφαιρετική, θεώρηση των πραγμάτων, η οποία να είναι ανεξάρτητη από τις φυσικές τους διαστάσεις. Η αδυναμία του παιδιού φαίνεται και από το γεγονός ότι την έννοια της διατήρησης των φυσικών αυτών μεγεθών δεν την κατακτά ταυτόχρονα για όλα, αλλά αλληλοδιαδόχως. Γίνεται δηλαδή, οριζόντια κλιμάκωση, μέσα στο ίδιο εξελικτικό στάδιο, του χρόνου απόκτησης των διαφόρων μορφών διατήρησης των διαστάσεων ενός ερεθίσματος. Έτσι, πρώτη κατακτάται η διατήρηση της ποσότητας (περί το 7^ο ή 8^ο έτος), στη συνέχεια η διατήρηση του βάρους (περί το 9^ο ή το 10^ο έτος) και τελευταία η διατήρηση του όγκου ( περί το 11^ο ή 12^ο έτος). (Εξελικτική ψυχολογία, Παρασκευοπούλου Ι., τόμος 3,4, σελ 66-67)

Ένα άλλο σημαντικό γνώρισμα-μειονέκτημα της σκέψης του παιδιού της σχολικής ηλικίας είναι ότι οι διάφορες συναγωγές των νοητικών πράξεων λειτουργούν μάλλον μεμονωμένα, δεν έχουν δηλαδή ακόμη οργανωθεί σε ένα ενιαίο, ευέλικτο και συνυπόλογο σύστημα που θα επέτρεπε τη θεώρηση ενός προβλήματος από όλες τις πλευρές του συγχρόνως. Το παιδί των 7 ως 11 ετών, ενώ κατέχει ήδη τους δυο κανόνες της αναστρεψιμότητας, την αναίρεση και την αντιστάθμιση, δεν μπορεί να συντονίσει ακόμα τους δυο αυτούς κανόνες ώστε να λειτουργούν υπό ένα ενιαίο σύστημα, όπως απαιτείται για τη λύση περίπλοκων προβλημάτων. Η ικανότητα αυτή θα εμφανιστεί μετά το 11^ο έτος, στην εφηβική ηλικία, με τις τυπικές ή αφαιρετικές, όπως λέγονται, νοητικές πράξεις. (Εξελικτική ψυχολογία, Παρασκευοπούλου Ι., τόμος 3,4, σελ 67)

Μέθοδοι που χρησιμοποίησε ο Piaget στα πειράματά του

Ο Piaget εξελίχθηκε σε ψυχολόγο στη δεκαετία του 1920. Διερεύνησε την κρυφή πλευρά του παιδικού μυαλού. Ισχυρίστηκε ότι τα παιδιά μετακινούνται από τη θέση του εγωκεντρισμού (egocentrism) στον κοινωνιοκεντρισμό (sociocentrism). Προς εξήγηση, συνδύασε τη χρήση ψυχολογικών κλινικών μεθόδων για να δημιουργήσει αυτό που ονόμασε ημικλινική (semiclinical) συνέντευξη. Ξεκίνησε τη συνέντευξη ζητώντας από τα παιδιά τυποποιημένες ερωτήσεις, και ανάλογα με τις απαντήσεις τους , έκανε μια σειρά μη τυποποιημένων ερωτήσεων. Ο Piaget αναζητούσε αυτό που ονόμασε "αυθόρμητη απόφαση" ("spontaneous conviction"), έτσι ώστε οι απαντήσεις που ζητούσε από τα παιδιά να μην είναι ούτε αναμενόμενες ούτε προβλέψιμες. Ωστόσο, ο Piaget αναγνώρισε τις δυσκολίες που υπάρχουν όταν παίρνει κανείς συνέντευξη από ένα παιδί και ότι είναι πολύ σημαντικό να γίνεται διάκριση μεταξύ των κατευθυνόμενων και των αυθόρμητων απαντήσεων. Στις έρευνές του, παρατήρησε ότι υπήρχε μια σταδιακή εξέλιξη από διαισθητικές σε επιστημονικές και κοινωνικά αποδεκτές απαντήσεις. Υποστήριξε ότι τα παιδιά το έκαναν αυτό εξαιτίας της κοινωνικής αλληλεπίδρασης και της επίδρασης των ιδεών μεγαλύτερων παιδιών, που βρίσκονταν σε πιο προχωρημένο επίπεδο. (el.wikipedia.org/wiki/Ζαν_Πιαζέ)

Μολαταύτα, ο Piaget θέλησε να επαναστατήσει όσον αφορά τον τρόπο με τον οποίο ήταν οργανωμένες οι ερευνητικές μέθοδοι. Παρόλο που ξεκίνησε την έρευνα με τους συνεργάτες του χρησιμοποιώντας την παραδοσιακή μέθοδο συλλογής στοιχείων (συνέντευξη) δεν ήταν πλήρως ευχαριστημένος με τα αποτελέσματα και θέλησε να συνεχίσει την προσπάθεια προκειμένου να βρει νέους τρόπους έρευνας, χρησιμοποιώντας ένα συνδυασμό στοιχείων, που περιλαμβάνουν : νατουραλιστική παρατήρηση, ψυχομετρία και ψυχιατρική κλινική εξέταση, με σκοπό να ακολουθήσει μία λιγότερο καθοδηγούμενη μορφή έρευνας με γνήσια αποτελέσματα. Η βασική ιδέα ήταν να παρατηρήσει πως τα παιδιά απαντούσαν σε ορισμένες περιπτώσεις για δικούς τους λόγους, προκειμένου να εξετάσει τις διαδικασίες της σκέψης τους. (el.wikipedia.org/wiki/Ζαν_Πιαζέ)

Ο Piaget κατάλαβε ότι τα ψυχομετρικά τεστ είχαν και τα όρια τους, καθώς τα παιδιά δεν ήταν ικανά να φανερώσουν στον ερευνητή τις ενδότερες σκέψεις και την εσωτερική νόησή τους. Επίσης, ήταν δύσκολο να γνωρίζει εάν τα αποτελέσματα των εξετάσεων ενός παιδιού αντανακλούσαν αυτό που πραγματικά πίστευαν τα παιδιά, ή εάν ήταν μόνο μια προσποιητή κατάσταση. Για παράδειγμα, είναι πολύ δύσκολο να γνωρίζει κανείς με σιγουριά, αν ένα παιδί που συζητά με ένα παιχνίδι πιστεύει ότι αυτό είναι ζωντανό ή απλά προσποιείται. Έπειτα από αρκετά συμπεράσματα σχετικά με τις ψυχομετρικές μελέτες, ο Piaget ξεκίνησε να αναπτύσσει την κλινική μέθοδο της εξέτασης. Η μέθοδος αυτή περιελάμβανε ερωτήσεις προς το παιδί και προσεκτική εξέταση των απαντήσεών του - προκειμένου να παρατηρήσει πως απαντούσε το παιδί σύμφωνα με τις ερωτήσεις που ζητούνταν - και μετά εξέταζε την αντίληψη του παιδιού σχετικά με τον κόσμο μέσα από τις απαντήσεις του. (el.wikipedia.org/wiki/Ζαν_Πιαζέ)