Σκοπός της παρούσας εργασίας είναι η παρουσίαση μίας εναλλακτικής διδακτικής πρότασης για τη διδασκαλία του πολλαπλασιασμού, η οποία εντάσσεται στο πλαίσιο της διερευνητικής μάθησης. Το «Μάθημα της Διερεύνησης» ορίζεται ως μία εκπαιδευτική καινοτομία που «συνίσταται στη διεξαγωγή ενός άτυπου σχολικού μαθήματος εστιασμένου στη βιωματική και επικοινωνιακή μαθησιακή διαδικασία, όπου διμελείς ή τριμελείς ομάδες μαθητών εκπονούν διερευνητικά συνεργατικά Projects. Βασική παράμετρος της διερευνητικής παιδαγωγικής και συνεπώς του συγκεκριμένου πονήματος, είναι η ένταξη και αξιοποίηση της ψηφιακής τεχνολογίας μέσα στο χώρο του σχολείου. Άλλωστε, οι νέες τεχνολογίες θεωρείται σήμερα ότι μπορούν να διαδραματίσουν θετικό ρόλο στην εκπαιδευτική διαδικασία, με βασική προϋπόθεση την τήρηση των προδιαγραφών που έχει ορίσει το παιδαγωγικό ινστιτούτο για το εκπαιδευτικό λογισμικό.

Ο κύριος στόχος της διδακτικής πρότασης είναι να αντιληφθούν τα παιδιά τον αλγόριθμο του πολλαπλασιασμού μέσα από τις οπτικές αναπαραστάσεις του. Η θεματική της εργασίας συνδέεται άμεσα με τη στοχοθεσία που ορίζει το Αναλυτικό Πρόγραμμα και χρησιμοποιεί την τεχνολογία τόσο για την αφήγηση του σεναρίου όσο και για την οπτικοποίηση του πολλαπλασιασμού. Η διδακτική παρέμβαση διάρκειας δύο διδακτικών ωρών (90 λεπτών), απευθύνεται σε μαθητές της τρίτης τάξης του δημοτικού, ηλικίας 9 ετών και πραγματοποιήθηκε στους 24 μαθητές των δύο τμημάτων του δημοτικού σχολείου Πορταριάς.

Στο εισαγωγικό κεφάλαιο της εργασίας επιχειρείται η ανάλυση της μαθηματικής έννοιας, δηλαδή του πολλαπλασιασμού και των ιδιοτήτων του, καθώς και τα αποτελέσματα που προέκυψαν από τη διεξαγωγή της άτυπης συνέντευξης. Στο επόμενο κεφάλαιο παρουσιάζονται αναλυτικά οι μαθησιακοί στόχοι που τέθηκαν και οι δραστηριότητες που οργανώθηκαν για την επίτευξή τους. Παράλληλα, δεν παραλείπεται να γίνει μία εκτενής και αναλυτική περιγραφή των υλικών που υποστήριξαν τις συγκεκριμένες δραστηριότητες. Στη συνέχεια, γίνεται η λεπτομερής παρουσίαση των βημάτων που ακολουθήθηκαν, ώστε να επιτευχθούν οι μαθησιακοί και γνωστικοί στόχοι. Στο τελευταίο κεφάλαιο, επιχειρείται η ανάλυση των αποτελεσμάτων και εξετάζεται ο ρόλος της ψηφιακής τεχνολογίας μέσα στο πλαίσιο της διδακτικής παρέμβασης.

Μαθηματική Έννοια και Δεξιότητες:

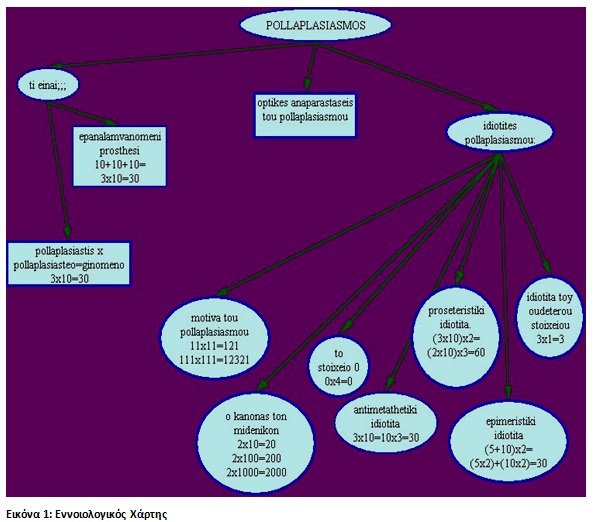
Η παρούσα εργασία θέτει στο επίκεντρο τη μαθηματική έννοια του πολλαπλασιασμού. Πιο συγκεκριμένα, εστιάζει στα αριθμητικά μοτίβα που προκύπτουν μέσα από τον πολλαπλασιασμό συγκεκριμένων αριθμών, στον κανόνα των μηδενικών και στις οπτικές αναπαραστάσεις του πολλαπλασιασμού. Δεν στρέφεται αυστηρά στην ορθότητα επιτέλεσης των αριθμητικών πράξεων με χαρτί και μολύβι. Αντίθετα, γίνεται προσπάθεια να αναδειχθεί ο τρόπος που τα παιδιά κατανοούν τις αριθμητικές πράξεις του πολλαπλασιασμού, ενώ παράλληλα υπάρχει ενδιαφέρον για τις μεθόδους που ακολουθούν, ώστε να φτάσουν στην επίλυση τους. Είναι γεγονός ότι ο αλγόριθμος του πολλαπλασιασμού θεωρείται ο δυσκολότερος από τους τέσσερις αλγόριθμους. Οι μαθητές δυσκολεύονται να κατανοήσουν τόσο τα σύνολα ως ξεχωριστές δομές, όσο και ότι ένα σύνολο αποτελείται από ένα δεδομένο αριθμό αντικειμένων. Ο Κώστας Ζαχαρός επισημαίνει:

«Ο Piaget (1965) υπογραμμίζει ότι ο πολλαπλασιασμός και η διαίρεση απαιτούν ικανότητες που βασίζονται σε ποιοτικές αλλαγές στην παιδική σκέψη. Στον προσθετικό συλλογισμό (additive reasoning), για παράδειγμα, που εμφανίζεται στα προβλήματα πρόσθεσης και αφαίρεσης με διάφορες μορφές, αντικείμενα ή σύνολα αντικειμένων ενώνονται ή διαχωρίζονται. Όμως ο πολλαπλασιαστικός συλλογισμός διαφέρει, γιατί δεν εμπλέκει μόνο τις πράξεις της ένωσης και του διαχωρισμού. Εδώ εμφανίζονται ποικίλα είδη συλλογισμών, όπως η αντιστοίχηση ένα προς πολλά, οι αναλογικές σχέσεις μεταξύ μεταβλητών, οι λειτουργίες διανομής, διαίρεσης και διαχωρισμού (Nunes & Bryant, 1996)»

Η απόκτηση της μαθηματικής γνώσης είναι μία «διαρκής διαδικασία επαναδόμησης», απαιτεί δηλαδή τον αναστοχασμό των μαθητών για να αναδιοργανώσουν τις γνώσεις τους και δεν αποτελεί μια γραμμική μαθησιακή εξέλιξη. Γι’ αυτό το λόγο πριν την εφαρμογή της διδακτικής παρέμβασης προηγήθηκε η άτυπη συνέντευξη. Στόχος μας ήταν η ανίχνευση των γνώσεων των μαθητών για τον πολλαπλασιασμό, για να μπορέσουμε στη συνέχεια να εισάγουμε τις νέες γνώσεις. Οι ερωτήσεις που τέθηκαν στόχευαν στη σύνδεση του πολλαπλασιασμού με τον αλγόριθμο της πρόσθεσης και στη συνέχεια με τις ιδιότητες του (επιμεριστική, προσεταιριστική, αντιμεταθετική, ιδιότητα του ουδέτερου στοιχείου και το ρόλο του μηδενός). Η άτυπη συνέντευξη πλαισιώθηκε από μια ιστορία, που δημιουργήθηκε με αφορμή το βιβλίο «Το πειραχτήρι των αριθμών». Η αφήγηση της ενέπλεκε την επίλυση προβλημάτων. Εξαιτίας του αριθμού των μαθητών η συνέντευξη δεν έγινε ατομικά, αλλά απευθυνόταν σε όλα τα παιδιά. Τα εποπτικά μέσα ενεργοποίησαν το ενδιαφέρον των μαθητών και προκάλεσαν τη συμμετοχή τους στη διαδικασία μάθησης. Η αφήγηση των περιπετειών των δύο πρωταγωνιστών κινητοποίησε την τάξη και διέγειρε την περιέργεια τους για την έκβαση της ιστορίας.

Σχεδιασμός Διδακτικής Παρέμβασης:

Η διδακτική παρέμβαση στηρίχθηκε στην βασική παραδοχή του κονστρουκτιβισμού ότι ο άνθρωπος συμμετέχει ενεργά στην κατασκευή της γνώσης και δεν τη δέχεται παθητικά. Επομένως, για να παραχθεί νέα γνώση χρειάζεται να προκύψει μια προβληματική κατάσταση που θα ενεργοποιήσει τις γνωστικές δομές για την επίλυση του προβλήματος. Η διδασκαλία που σχεδιάστηκε στοχεύει στην παροχή ευκαιριών και την ενθάρρυνση του μαθητή να κατασκευάζει μόνος του τις μαθηματικές γνώσεις, μέσα από την εξερεύνηση, τον πειραματισμό, το σχηματισμό υποθέσεων και την αιτιολόγηση. Όλα τα παραπάνω συντελούν στην επίτευξη της ουσιαστικής μάθησης.

Ο αναλυτικός σχεδιασμός της διδασκαλίας θεωρείται κάτι παραπάνω από αναγκαίος και οφείλει να στηρίζεται όχι μόνο στο διδακτικό εγχειρίδιο, αλλά να ενσωματώνει πρόσθετο υλικό του εκπαιδευτικού, εκπληρώνοντας πάντα τους στόχους του αναλυτικού προγράμματος Επιπλέον, είναι σκόπιμο να καθορίζει το ρόλο του μαθητή και του διδάσκοντα και να πλαισιώνεται από ποικίλα ενισχυτικά διδακτικά μέσα, όπως η ψηφιακή τεχνολογία. Τέλος, είναι σημαντικό να εμπλέκει βιωματικά τους μαθητές και να ενεργοποιεί περισσότερες από μία αισθήσεις, καθώς με αυτό τον τρόπο επιτυγχάνεται η κατανόηση του διδασκόμενου αντικειμένου.

Στόχοι και Δραστηριότητες:

Άξονες Διδακτικής Παρέμβασης:

Οι άτυπες γνώσεις και οι εμπειρίες των παιδιών αποτελούν το εφαλτήριο για το σχεδιασμό της διδακτικής παρέμβασης. Σημαντικό ρόλο παίζει το σενάριο που την πλαισιώνει καθώς ενεργοποιεί το ενδιαφέρον τους. Η οργάνωση των μαθησιακών δραστηριοτήτων βασίστηκε στους παρακάτω τέσσερις άξονες:

• Πλαισιοθέτηση: Η εισαγωγή στην έννοια του πολλαπλασιασμού στηρίζεται στην αφήγηση μιας φανταστικής ιστορίας. Οι περιπέτειες των δύο πρωταγωνιστών, του Ρόμπερτ και του Αριθμούλη, εισάγουν τα παιδιά στην έννοια του πολλαπλασιασμού.

• Αναπαράσταση: Η οπτική αναπαράσταση της ιστορίας, μέσα από την προβολή της σε προτζέκτορα -εμπλουτισμένη τόσο με εικόνες όσο και με κείμενο- και η δική μας αφηγηματική επένδυση, δίνει φωνή στους δύο πρωταγωνιστές. Η αλληλεπίδραση μαθητών και πρωταγωνιστών είναι συνεχής κατά τη διάρκεια της άτυπης συνέντευξης. Η απάντηση στα ερωτήματα, προωθεί την εξέλιξη της ιστορίας.

• Μαθηματικοποίηση: Διατηρώντας το θεματικό πλαίσιο της άτυπης συνέντευξης, σχεδιάστηκαν δύο δραστηριότητες. Η πρώτη δραστηριότητα περιλαμβάνει δύο αποστολές/φύλλα εργασίας, όπου τα παιδιά μέσα από τη διερευνητική μάθηση καλούνται να ανακαλύψουν τον κανόνα των μηδενικών και εν συνεχεία να αναγνωρίζουν τα αριθμητικά μοτίβα που προκύπτουν από τον πολλαπλασιασμό συγκεκριμένων αριθμών. Η δεύτερη δραστηριότητα αποσκοπεί στην οπτική αναπαράσταση του πολλαπλασιασμού, διαμεσολαβημένη από την ψηφιακή τεχνολογία (virtual manipulatives).

• Δημοσιοποίηση: Η δημοσιοποίηση πραγματοποιείται με την οργάνωση της αξιολόγησης των δραστηριοτήτων. Η αξιολόγηση κάνει εμφανή την κατάκτηση των γνωστικών στόχων, αλλά και τη διάγνωση των δυσκολιών που προέκυψαν κατά τη διάρκεια των δραστηριοτήτων.

Ανάλυση Μαθησιακών Δραστηριοτήτων:

Το αρχικό στάδιο της διδακτικής παρέμβασης στηρίζεται στο σαφή και ρεαλιστικό ορισμό της στοχοθεσίας. Ως συνέπεια, ο εκπαιδευτικός καλείται να θέσει από τη μία πλευρά τους γενικούς και από την άλλη τους ειδικούς διδακτικούς στόχους.

Σκοποί:

1. Να αντιληφθούν τον αλγόριθμο του πολλαπλασιασμού φυσικών μονοψήφιων ή πολυψήφιων αριθμών.

1. Να κατανοούν και να χρησιμοποιούν τις ιδιότητες του πολλαπλασιασμού, όπως τον επιμερισμό του πολλαπλασιασμού ως προς την πρόσθεση.

1. Να κατανοούν ότι όταν μιλάμε για το εμβαδό ενός σχήματος, εννοούμε το μήκος επί το πλάτος και ότι σε αυτό μας βοηθάει ο πολλαπλασιασμός.

1. Να αναπτύξουν επικοινωνιακές δεξιότητες (συνεργασία, εργασία σε ομάδες) μέσα από τη χρήση αναπαραστατικών μέσων.

1. Να αναπτύξουν στρατηγικές ελέγχου και επαλήθευσης.

Δραστηριότητα 1^η

«Δε με φοβίζουν οι μεγάλοι αριθμοί»

Στόχοι:

1. Να αναγνωρίσουν τα αριθμητικά μοτίβα που προκύπτουν από τον πολλαπλασιασμό συγκεκριμένων αριθμών.

1. Να χρησιμοποιήσουν τα αριθμητικά μοτίβα, ώστε να επιλύουν τους πολλαπλασιασμούς με το μυαλό.

Πορεία: Η διδακτική παρέμβαση ξεκινά με την εξέλιξη της ιστορίας του «Ρόμπερτ και του Αριθμούλη» που πλαισίωσε την άτυπη συνέντευξη, ώστε να επιτευχθεί η σύνδεση και η ομαλή εισαγωγή στη διδασκαλία. Στη συνέχεια, ο εκπαιδευτικός μοιράζει στους μαθητές τα δύο φύλλα εργασίας. Παροτρύνει τα παιδιά να δουλέψουν τις ασκήσεις με το μυαλό, αλλά επιτρέπει τη χρήση υπολογιστικής μηχανής σε όποιον το επιθυμεί. Ενθαρρύνει τα παιδιά να σκεφτούν τον τρόπο επίλυσης των ασκήσεων, παρατηρώντας τι αλλάζει κάθε φορά στους αριθμούς που προκύπτουν. Προκαλεί παράλληλα το δημόσιο διάλογο, κοινοποιώντας την απορία κάποιου μαθητή στους υπόλοιπους.

Αξιολόγηση: Καλούμε τα παιδιά να απαντήσουν στις ερωτήσεις που υπάρχουν στις κάρτες τους, μετά το τέλος των ασκήσεων. Ερωτήσεις όπως «Τι παρατηρείς;» «Τι αλλάζει στους αριθμούς που προέκυψαν;» επιτρέπουν στον εκπαιδευτικό να αξιολογήσει την κατάκτηση των παραπάνω γνωστικών στόχων και να διαγνώσει τον τρόπο σκέψης των παιδιών.

Δραστηριότητα 2^η

«Μετατρέπω τον πολλαπλασιασμό σε σχήματα»

1. Να συνδέσουν την πράξη του πολλαπλασιασμού με τις οπτικές αναπαραστάσεις του (κυβάκια)

1. Να πειραματιστούν με το λογισμικό virtual manipulatives

1. Να αποδώσουν στο virtual manipulatives, τις οπτικές αναπαραστάσεις συγκεκριμένων πολλαπλασιασμών

Πορεία: Συνεχίζουμε την προβολή της ιστορίας για να είναι ομαλή η μετάβαση στη δεύτερη δραστηριότητα. Οι δύο πρωταγωνιστές, ο Ρόμπερτ και ο Αριθμούλης, συνδέουν τον πολλαπλασιασμό με τις οπτικές αναπαραστάσεις του. Έπειτα, ο εκπαιδευτικός παροτρύνει τα παιδιά να πειραματιστούν σε ομάδες με το virtual manipulatives, ώστε να κατανοήσουν τη δομή του προγράμματος. Μετά το στάδιο του πειραματισμού τους δίνει συγκεκριμένα γινόμενα και τους ζητά να τα αποτυπώσουν στο πρόγραμμα. Αρχικά, τα γινόμενα αφορούν τον πολλαπλασιασμό μονοψήφιων αριθμών και αργότερα διψήφιων αριθμών. Έπειτα, ο εκπαιδευτικός ζητά από τις ομάδες να δουλέψουν συνεργατικά, αναπαριστώντας οπτικά, διάφορα γινόμενα που θέτει ο ένας μαθητής στον άλλο. Ενθαρρύνει επίσης τη μεταξύ τους συζήτηση ώστε να οπτικοποιηθούν επιτυχώς οι πολλαπλασιασμοί.

Αξιολόγηση: Ο εκπαιδευτικός μοιράζει στους μαθητές τα φύλλα αξιολόγησης που περιλαμβάνουν την μετατροπή των οπτικών αναπαραστάσεων σε πράξεις πολλαπλασιασμού και το αντίθετο.

Ψηφιακά και μη ψηφιακά υλικά:

Η χρήση του ψηφιακού και μη ψηφιακού υλικού στηρίζει ουσιαστικά ολόκληρη τη δομή και την ανάπτυξη των δραστηριοτήτων. Η οπτικοποίηση του σεναρίου με τη βοήθεια του προτζέκτορα, οι αριθμομηχανές και το λογισμικό virtual manipulatives αποτελούν τα μέσα για την αποσαφήνιση της μαθηματικής έννοιας του πολλαπλασιασμού και την κατάκτηση των γνωστικών στόχων που τέθηκαν.

Οι αριθμομηχανές σχετίζονται άμεσα με τις καθημερινές βιωματικές εμπειρίες των παιδιών, αν και μέσα στο σχολικό πλαίσιο συνοδεύονται από στερεότυπα που αποτρέπουν παρά ενθαρρύνουν τη χρήση τους (πχ τα παιδιά τεμπελιάζουν, δεν σκέφτονται). Εντούτοις, σήμερα πολλοί συμφωνούν ότι η σωστή χρήση της αριθμομηχανής μέσα στο πλαίσιο μιας διδακτικής παρέμβασης μπορεί να συμβάλει στην εμπέδωση των μαθηματικών. Μακροχρόνιες μελέτες άλλωστε έχουν αποδείξει ότι οι μαθητές που τις χρησιμοποίησαν βελτίωσαν σημαντικά την εννοιολογική κατανόηση μαθηματικών εννοιών και την ικανότητα επίλυσης προβλημάτων. Με αυτή τη λογική εντάχθηκαν στη δραστηριότητα, εξυπηρετώντας τους σκοπούς της διερεύνησης και του πειραματισμού.

Όσο αφορά το virtual manipulatives, πρόκειται για ένα ψηφιακό περιβάλλον, η πρόσβαση στο οποίο δίνει τη δυνατότητα ανάπτυξης επιμέρους μαθηματικών δεξιοτήτων. Ο τρόπος χρήσης του λογισμικού στην δραστηριότητα που περιγράφηκε παραπάνω, δεν απαιτούσε ιδιαίτερες τεχνικές δεξιότητες των μαθητών. Η πρόσβαση σε αυτό είναι ιδιαίτερα απλή και σε καμιά περίπτωση δεν απαιτεί κάποιου είδους εξάσκηση. Η κίνηση του ποντικιού αποτελεί ουσιαστικά την εντολή του χρήστη για την επιτέλεση των πράξεων του πολλαπλασιασμού, οι οποίες αποτυπώνονται στο δεξί μέρος της οθόνης. Το virtual manipulatives εντάσσεται στις «ανοιχτές τεχνολογίες μάθησης», δηλαδή στα περιβάλλοντα εκείνα που παρέχουν στο χρήστη αυτονομία και επιτρέπουν τη δημιουργική σχεδίαση δραστηριοτήτων. Πιο συγκεκριμένα πρόκειται για ένα λογισμικό δυναμικής γεωμετρίας, το οποίο υποστηρίζει τον στόχο της συγκεκριμένης διδακτικής παρέμβασης, δηλαδή τη σύνδεση του πολλαπλασιασμού με την οπτική αναπαράστασή του. Η υλοποίηση των διδακτικών στόχων χωρίς τη χρήση του συγκεκριμένου λογισμικού θα μπορούσε να επιτευχθεί με την ένταξη στη δραστηριότητα απτικού υλικού (κυβάκια), εναλλακτική που θα παρείχε στους μαθητές τη δυνατότητα της βιωματικής εμπλοκής τους και δεν θα υποβάθμιζε το ρόλο της οπτικής αναπαράστασης. Είναι γεγονός πάντως πως η χρήση του ηλεκτρονικού υπολογιστή στη μαθησιακή διαδικασία καθιστά το γνωστικό αντικείμενο πιο ελκυστικό.

Η τεχνολογία μέσα στο πλαίσιο μιας σχολικής τάξης λειτουργεί υποστηρικτικά προς τους μαθητές τόσο με άμεσο όσο και με έμμεσο τρόπο. Η άμεση προσφορά του στην ανάπτυξη της μαθηματικής έννοιας του πολλαπλασιασμού εντοπίζεται στη σύνδεση των πράξεων πολλαπλασιασμού με την οπτική αποτύπωση τους. Η αναπαράσταση ενός γινόμενου με τη μορφή ενός σχήματος, οπτικοποιεί μια αφηρημένη μαθηματική πράξη. Το ψηφιακό υλικό αποτελεί το διαμεσολαβητικό μέσο που μετατρέπει το αφηρημένο σε συγκεκριμένο, που εντάσσει τον πολλαπλασιασμό στην πρακτική εφαρμογή της καθημερινότητας. Από την άλλη πλευρά, η ενασχόληση των μαθητών με το λογισμικό μέσα από την ομαδική εργασία, δημιουργεί κλίμα συνεργατικότητας και τους προσφέρει τη δυνατότητα να συνδιαλέγουν, να διαφωνήσουν, να συμφωνήσουν και στο τέλος να αναπαραστήσουν το γινόμενο δύο αριθμών. Η ανάληψη συγκεκριμένων κάθε φορά ρόλων από τους μαθητές κάνει τη μάθηση δημιουργική. Εντούτοις, ο σχεδιασμός και η εφαρμογή μιας διδασκαλίας δεν βρίσκονται πάντα σε πλήρη αρμονία. Είναι πιθανό η δυνατότητα αυτενέργειας που δίνεται στους μαθητές να δημιουργήσει προβλήματα σε ομαδοσυνεργατικό επίπεδο και να μην γίνουν σεβαστοί οι κανόνες που τίθενται από τον εκπαιδευτικό ως προς τη χρήση του λογισμικού και την ανάληψη ρόλων από τους μαθητές.

Μάθηση και Δράσεις Παιδιών:

Κομβικό σημείο στο σχεδιασμό μιας διδακτικής παρέμβασης αποτελεί η εκ των προτέρων ανάλυση των αλληλεπιδράσεων ανάμεσα στους μαθητές που ο εκπαιδευτικός επιθυμεί να προκαλέσει. Παράλληλα, μεγάλη σημασία έχει να ανιχνευθεί ο τρόπος που οι αλληλεπιδράσεις αυτές θα επηρεάσουν τη μάθηση των παιδιών. Επιχειρώντας την κατηγοριοποίηση των αλληλεπιδράσεων, μπορούμε να ισχυριστούμε ότι μπορούν να λάβουν τις εξής διαστάσεις, τις λεκτικές αλληλεπιδράσεις και τις κοινωνικές αλληλεπιδράσεις.

Στο πλαίσιο των λεκτικών αλληλεπιδράσεων, τα ερωτήματα της άτυπης συνέντευξης, που έχουν ως στόχο να διερευνήσουν τις ανάγκες και τις εμπειρίες των παιδιών αναδύονται μέσα από την αφήγηση του σεναρίου και ουσιαστικά τίθενται δια στόματος των δύο πρωταγωνιστών. Δεν είναι όμως μόνο προφορικά αλλά προβάλλονται μέσω του PowerPoint. Ουσιαστικά, προσπαθούν να ανιχνεύσουν τις γνώσεις των μαθητών για τον πολλαπλασιασμό και τις ιδιότητές του. Οι ερωτήσεις δεν είναι αποκομμένες από την υπόθεση της ιστορίας, αλλά απόλυτα ενταγμένες σε αυτή. Η απάντηση των παιδιών στους γρίφους της ιστορίας επιτρέπει τη συνέχιση της. Τα ερωτήματα της πρώτης δραστηριότητας διατυπώνονται γραπτά και εμπλέκουν τα παιδιά σε μια διαδικασία αναστοχασμού. Έχουν σκοπό να ανιχνεύσουν τις μεταγνωστικές ικανότητες των μαθητών, επιτρέποντας τους να αναλογιστούν τον τρόπο που τους οδήγησε στα συγκεκριμένα αποτελέσματα. Τέλος, τα ερωτήματα της δεύτερης δραστηριότητας τίθενται προφορικά από τον εκπαιδευτικό αλλά και από μαθητή σε μαθητή.

Στο πλαίσιο των κοινωνικών αλληλεπιδράσεων η οργάνωση της τάξης έγινε με τέτοιο τρόπο ώστε να επιτρέπει ταυτόχρονα δράσεις των παιδιών ομαδικές και ατομικές. Η άτυπη συνέντευξη ενθαρρύνει το δημόσιο διάλογο μέσα στην τάξη και δεν αφορά κάθε μαθητή ατομικά. Η πρώτη δραστηριότητα επιτρέπει την ατομική δράση του μαθητή ώστε να διαπιστωθεί η εμπέδωση του γνωστικού αντικειμένου. Η δεύτερη δραστηριότητα είναι ομαδική, επιβάλλει τη συνεργασία της ομάδας, την εναλλαγή ρόλων (κάποιος ρωτάει, κάποιος δημιουργεί τα σχήματα στο virtual manipulatives) και την κοινή προσπάθεια για την κατανόηση της οπτικής αναπαράστασης του πολλαπλασιασμού.

Πίνακας 1: Ανάλυση μαθησιακών δραστηριοτήτων

Εφαρμογή στην πράξη μιας διδακτικής παρέμβασης:

Για να συλλέξουμε και να καταγράψουμε τα δεδομένα, χρησιμοποιήσαμε φύλλα παρατήρησης (παραθέτονται στο παράρτημα), βιντεοκάμερα με την οποία καταγράψαμε την άτυπη συνέντευξη και την εφαρμογή των δραστηριοτήτων και δεν λησμονήσαμε, η κάθε μία από μας, να κρατήσει προσωπικό ημερολόγιο, καθ’ όλη τη διάρκεια των διάφορων φάσεων. Επίσης, καθώς εξελισσόταν αρχικά η άτυπη συνέντευξη και στη συνέχεια η διδακτική παρέμβαση, παρατηρούσαμε την πρόοδο των παιδιών και την συμμετοχή τους στο μάθημα, το κατά πόσο ανταποκρίνονταν στα ερεθίσματα μας και πόσο πρόθυμα ήταν να πειραματιστούν ή να εκφράσουν τους προβληματισμούς τους.

H σχολική τάξη και τα παιδιά:

Το σχολείο που πραγματοποιήσαμε την άτυπη συνέντευξη και τη διδακτική παρέμβαση ήταν το Ολοήμερο Δημοτικό Πειραματικό Σχολείο Πορταριάς Πηλίου. Διέθετε μεγάλο προαύλιο χώρο, όπου τα παιδιά είχαν την δυνατότητα να ψυχαγωγούνται και να αλληλεπιδρούν, ένα χώρο πολυμέσων με προτζέκτορα, όπου εκεί πραγματοποιήθηκαν η άτυπη συνέντευξη και η διδακτική παρέμβαση και μία αίθουσα υπολογιστών για τα μαθήματα πληροφορικής και για την εξάσκηση των παιδιών στον χειρισμό των ηλεκτρονικών υπολογιστών.

Η τάξη δεν ήταν ιδιαίτερα ευρύχωρη, δε διέθετε γωνιές και τα τραπεζάκια, όπου κάθονταν τα παιδιά σε ομάδες, σχημάτιζαν νοερά ένα τετράγωνο. Στην άκρη της τάξης υπήρχαν παγκάκια που προφανώς εξυπηρετούσαν περιστασιακές ανάγκες σε περίπτωση έλλειψης χώρου. Το σύνολο των παιδιών των δύο τμημάτων της τρίτης δημοτικού ήταν συνολικά 24, αλλά την ημέρα της διδακτικής παρέμβασης ήταν παρόντα 23. Τα δυο τμήματα της τρίτης τάξης διέθεταν αγόρια και κορίτσια ηλικίας 8 χρονών, με ένα ποσοστό αλλοδαπών παιδιών. Το κοινωνικο-οικονομικό επίπεδο των οικογενειών των παιδιών ήταν καλό.

Τα παιδιά ανέπτυξαν κοινές εμπειρίες για τη μαθηματική έννοια του πολλαπλασιασμού, μέσω της άτυπης συνέντευξης που πραγματοποιήθηκε δύο μέρες πριν εφαρμοστεί η διδακτική παρέμβαση. Αφού είχαμε αξιολογήσει το επίπεδο των παιδιών ως προς την έννοια του πολλαπλασιασμού και τις ιδιότητες του -μέσω της εξιστόρησης του παραμυθιού με ήρωες τον Αριθμούλη και τον Ρόμπερτ- φροντίσαμε να σχεδιάσουμε ανάλογα την διδακτική παρέμβαση, ώστε να είναι ευχάριστη και να μην είναι αποκομμένη από το σενάριο της άτυπης συνέντευξης. Ο Ρόμπερτ λοιπόν ανέθεσε αποστολές στα παιδιά προκειμένου να τον βοηθήσουν να μάθει τον πολλαπλασιασμό καλύτερα.

Σκοπός της διδακτικής παρέμβασης ήταν να κατανοήσουν τα παιδιά την έννοια του πολλαπλασιασμού και τις ιδιότητες του. Για την επίτευξή του χρησιμοποιήθηκαν υλικά και εποπτικά μέσα (αριθμομηχανή και ηλεκτρονικός υπολογιστής). Η διδακτική παρέμβαση απαιτούσε τη συμμετοχή όλων των παιδιών είτε σε ομάδες ή είτε ως μονάδες. Και στις δύο περιπτώσεις τα παιδιά μπορούσαν να συνεργαστούν, να συμφωνήσουν ή να ανταλλάξουν απόψεις, δοκιμάζοντας ακόμα και το λάθος και επαληθεύοντας το αποτέλεσμα με πολλούς διαφορετικούς τρόπους.

Η συνολική διάρκεια της διδακτικής παρέμβασης ήταν 55 λεπτά. Βασιστήκαμε σε 4 βασικούς άξονες σχεδιασμού:

• Γνωριμία και ανάλυση της μαθηματικής έννοιας του πολλαπλασιασμού, μέσω της άτυπης συνέντευξης και της διερεύνησης των γνώσεων.

• Σχεδιασμός διδακτικής παρέμβασης / επιλογή κατάλληλου λογισμικού σύμφωνα με το επίπεδο των παιδιών και τις ήδη κατεκτημένες γνώσεις.

• Εφαρμογή διδακτικής παρέμβασης και χρησιμοποίηση του ανάλογου λογισμικού.

• Αξιολόγηση ως προς την πορεία εξέλιξης της διδακτικής παρέμβασης και ως προς το τι κατέκτησαν τα παιδιά– αναστοχασμός τι πήγε καλά και τι δεν πήγε καλά.

Διαδικασίες εφαρμογής της διδακτικής παρέμβασης:

Όταν επισκεφτήκαμε τον χώρο του σχολείου, χρειάστηκε να γίνουν κάποιες σημαντικές αλλαγές στον αρχικό σχεδιασμό μας. Ενώ είχαμε εξασφαλίσει την αίθουσα των υπολογιστών και είχαμε συμφωνήσει με τις εκπαιδευτικούς των δύο τάξεων ως προς την διαθεσιμότητα και την καταλληλότητα της, τελικά δεν κατέστει δυνατό να την χρησιμοποιήσουμε. Καθυστερημένα, οι εκπαιδευτικοί μας πληροφόρησαν ότι ο χώρος δεν θα επαρκούσε για να συμπληρωθούν τα φύλλα εργασίας και ότι η αίθουσα υπολογιστών δεν διέθετε προτζέκτορα τον οποίο εμείς χρειαζόμασταν προκειμένου να προβάλουμε την εξέλιξη του παραμυθιού.

Συγκεντρώσαμε τελικά τα δύο τμήματα της τρίτης τάξης του δημοτικού και μεταφερθήκαμε ξανά, όλοι μαζί στην αίθουσα που διέθετε έναν ηλεκτρονικό υπολογιστή και έναν προτζέκτορα, εκεί όπου είχε διεξαχθεί και η άτυπη συνέντευξη. Αξίζει να σημειωθεί ότι για την εφαρμογή της διδακτικής παρέμβασης χρειάστηκαν ακόμα 3 προσωπικοί υπολογιστές/λάπτοπ. Ο χώρος δεν ήταν επαρκής, ώστε να χωράει τα 23 παιδιά των δύο τάξεων. Σε κάθε θρανίο υπήρχε ένας υπολογιστής όπου τα παιδιά έπρεπε να τον χρησιμοποιούν προσεκτικά εκ περιτροπής, με αποτέλεσμα να αλλάζουν θέση μεταξύ τους συνεχώς, κάτι που δεν βοηθούσε την ομαλή εξέλιξη της διδακτικής παρέμβασης. Έτσι, ενώ τα παιδιά θα μπορούσαν να δουλεύουν σε ομάδες τις οποίες εμείς πιο εύκολα θα μπορούσαμε να κατευθύνουμε και να παρατηρούμε, ο χώρος δεν επέτρεψε κάτι τέτοιο. Η αναταραχή ήταν μεγάλη και η δραστηριότητα δεν εφαρμόστηκε σε ένα περιβάλλον οικείο και ήσυχο, κατάλληλο για την προώθηση της γνώσης και της μάθησης.

Εφόσον συγκεντρώσαμε τα 23 παιδιά στην αίθουσα των πολυμέσων, προβάλλαμε στα παιδιά τη συνέχεια της ιστορίας, όπου ο Ρόμπερτ αναθέτει στα παιδιά αποστολές προκειμένου να τον βοηθήσουν να αντιληφθεί τον κανόνα των μηδενικών και τα αριθμητικά μοτίβα που προκύπτουν από συγκεκριμένους πολλαπλασιασμούς, κάνοντας πράξεις, υπολογίζοντας γινόμενα, με ή χωρίς την βοήθεια του Αριθμομηχανούλη, δηλαδή της αριθμομηχανής. Τα παιδιά είχαν τη δυνατότητα να την χρησιμοποιήσουν, αν τυχόν δυσκολεύονταν να υπολογίσουν με το μυαλό τους κάποια από τα γινόμενα. Τα παιδιά αρχικά δυσανασχέτησαν με τα φύλλα εργασίας. Μοιράσαμε στο κάθε παιδί από ένα φύλλο εργασίας και εξηγήσαμε τι πρέπει να κάνουν.

Η πρώτη αποστολή-δραστηριότητα που έθεσε ο Ρόμπερτ στους μαθητές ήταν να υπολογίσουν κάποια γινόμενα διψήφιων αριθμών, κάνοντας πολλαπλασιασμό, είτε με το μυαλό είτε με την αριθμομηχανή, και τέλος ως αξιολόγηση, στο ίδιο φυλλάδιο καλούνταν να απαντήσουν σε ερωτήσεις όπως το τι παρατηρούν ως προς τα γινόμενα και τους αριθμούς που σχηματίζονται και να καταγράψουν τι συμπεραίνουν. Στόχοι αυτής της δραστηριότητας ήταν να ανακαλύψουν τον κανόνα των μηδενικών και να χρησιμοποιήσουν τον κανόνα των μηδανικών για να πολλαπλασιάσουν διαφόρους αριθμούς με το 10, το 100, το 1.000, το 1.000.000.000.

Αφού ολοκλήρωσαν το πρώτο φύλλο εργασίας, τους μοιράσαμε και το δεύτερο φύλλο, το οποίο ήταν στο ίδιο ύφος, και καλούσε τα παιδιά να συμπληρώσουν κάποια γινόμενα τριψήφιων ή και μεγαλύτερων αριθμών. Στόχοι αυτής της δραστηριότητας ήταν να αναγνωρίσουν τα αριθμητικά μοτίβα που προκύπτουν από τον πολλαπλασιασμό συγκεκριμένων αριθμών και να χρησιμοποιήσουν τα αριθμητικά μοτίβα, ώστε να επιλύουν τους πολλαπλασιασμούς με το μυαλό.

Και στα δύο φύλλα εργασίας που δόθηκαν στην πρώτη δραστηριότητα –αποστολή, κάποια παιδιά χρησιμοποίησαν την αριθμομηχανή και εξέφρασαν ενστάσεις γιατί δεν γνωρίζουν αριθμούς όπως το 1.000.000 ή να πολλαπλασιάζουν τριψήφιους με τριψήφιους ή πολυψήφιους. Οι αριθμομηχανές ήταν λιγότερες από τον αριθμό των παιδιών και έτσι έπρεπε να τις χρησιμοποιούν συνεργατικά, γεγονός που ενεργοποίησε τη συζήτηση και τελικά προκάλεσε φασαρία και σύγχυση.

Στην συνέχεια, η προβολή της ιστορίας στον προτζέκτορα έδειχνε τον Ρόμπερτ να βρίσκεται σε μια θαυμάσια λιλιπούτεια κυβο-χώρα γεμάτη κυβάκια. Όλα ήταν κυβάκια, οι καραμέλες τα ζαχαρωτά… Έτσι θέλαμε να εντάξουμε ομαλά τα παιδιά στην οπτική απεικόνιση του πολλαπλασιασμού, όπως αυτή δίνεται μέσω του εμβαδού (ύψος επί πλάτος). Στην ιστορία δινόταν κάποια εύκολα γινόμενα να τα υπολογίσουν τα παιδιά, μετρώντας στον προτζέκτορα-πίνακα τα κυβάκια και στην συνέχεια υπολογίζοντας το αποτέλεσμα.

Έτσι παρακινήσαμε τα παιδιά να περάσουν στη συνέχεια στους υπολογιστές. Εκεί, είχαμε εγκαταστήσει νωρίτερα το demo του virtual manipulatives. Πιο συγκεκριμένα, εισάγαμε τα παιδιά στον ιστότοπο που αναφέρεται στον πολλαπλασιασμό και στην οπτική του απεικόνιση. Εκεί τα παιδιά, είχαν την δυνατότητα αρχικά να πειραματιστούν με τα γινόμενα και τις οπτικές αναπαραστάσεις που σχηματίζουν, κατευθύνοντας το ποντίκι σωστά και μεθοδευμένα, ώστε να καταλήξουν στα επιδιωκόμενα αποτελέσματα. Στη συνέχεια, δίνονταν προφορικά από εμάς, κάποια τυχαία γινόμενα σε κάθε παιδί με σκοπό για να τα αναπαραστήσει στον υπολογιστή με τη βοήθεια του ποντικιού.

Στόχοι αυτής της δραστηριότητας ήταν να συνδέσουν την πράξη του πολλαπλασιασμού με τις οπτικές αναπαραστάσεις του (κυβάκια), να πειραματιστούν με το λογισμικό virtual manipulatives και να αποδώσουν στο virtual manipulatives, τις οπτικές αναπαραστάσεις συγκεκριμένων γινομένων. Σε αυτή την δραστηριότητα τα παιδιά συνεργάστηκαν επιτυχώς, αντάλλαξαν απόψεις, περίμεναν υπομονετικά την σειρά τους και κάποια από αυτά θέλησαν να σχηματίσουν παραπάνω από ένα γινόμενα, παίζοντας με το ποντίκι ή συμβουλευόμενα κάποιο συμμαθητή τους πώς να το κάνει. Στην συνέχεια ως αξιολόγηση, μοιράσαμε στα παιδιά φύλλα εργασίας στα οποία καλούνταν να ζωγραφίσουν τα τετραγωνάκια, σύμφωνα με το γινόμενο που τους δινόταν από κάτω και να συμπληρώσουν το αποτέλεσμα. Σε ένα δεύτερο φύλλο αξιολόγησης, τα παιδιά καλούνταν να γράψουν το γινόμενο των αριθμών, αφού μετρήσουν τα κυβάκια που ήταν ήδη γραμμοσκιασμένα και σχηματισμένα στο μιλιμετρέ χαρτί. Έτσι μπορούσαμε να αξιολογήσουμε τι αποκόμισαν τα παιδιά από την οπτική αναπαράσταση των γινομένων και πως τη σχηματοποίηση τους σε κυβάκια. Με αυτές τις δραστηριότητες ολοκληρώθηκε η διδακτική παρέμβαση στα δύο τμήματα της τρίτης Δημοτικού.

Προκειμένου να υλοποιηθεί επιτυχώς η διδακτική παρέμβαση, έπρεπε να προβούμε σε συνεννοήσεις που αφορούσαν το πού θα γινόταν η διδακτική παρέμβαση, σε ποια τάξη, πώς θα γινόταν, πόσο θα διαρκούσε, σε τι αναφερόταν. Καθ’ όλη τη διάρκεια της εφαρμογής της δραστηριότητας οι δύο εκπαιδευτικοί των τμημάτων της τρίτης Δημοτικού ήσαν παρούσες, ρωτούσαν τι πρέπει να κάνουν τα παιδιά, αν είναι σωστό που χρησιμοποιούν αριθμομηχανή, πως πρέπει να κάνουν τους υπολογισμούς των γινομένων και πως είναι δύσκολο για αυτά να κάνουν πολλαπλασιασμούς πολυψήφιων αριθμών, αφού δεν έχουν διδαχθεί. Η παρέμβαση αυτή σε συνδυασμό με τον ακατάλληλο χώρο είχε ως αποτέλεσμα να «σαμποτάρει» ως ένα βαθμό ολόκληρη τη φιλοσοφία της διδασκαλίας μας που ήταν η διερευνητική μάθηση. Ωστόσο και οι ίδιες διαπίστωσαν ότι ο χώρος ήταν μικρός σε σχέση με τον αριθμό των παιδιών και πως ήταν δύσκολο να λειτουργήσουμε αποτελεσματικά σε ένα τόσο περιοριστικό πλαίσιο σε συνδυασμό κιόλας με την απουσία πρότερης επαφή με το διδακτικό αντικείμενο και με παιδιά αυτής της ηλικίας.