Μια πρόταση διδακτικής παρέμβασης με το Cabri-geometry II σε παιδιά προσχολικής ηλικίας
Submitted by ltme on Wed, 07/23/2014 - 23:43Η παρούσα εργασία εντάσσεται στα πλαίσια της κατεύθυνσης του Ηλεκτρονικού Παιδαγωγικού Υλικού του Προγράμματος Μεταπτυχιακών Σπουδών. Σκοπός της εργασίας μας ήταν να οργανώσουμε, να πραγματοποιήσουμε και να αξιολογήσουμε μια διδακτική παρέμβαση, κάνοντας χρήση ενός εκπαιδευτικού λογισμικού. Αποφασίσαμε λοιπόν, να χρησιμοποιήσουμε το λογισμικό Cabri-Geometry II σε παιδιά προσχολικής εκπαίδευσης, γιατί μας ενδιέφερε ν’ ανακαλύψουμε το πώς θα λειτουργήσουν τα παιδιά αυτής της ηλικίας με αυτό, μιας και το Cabri απευθύνεται σε μαθητές γυμνασίου και λυκείου. Μέλημά μας ήταν να σχεδιάσουμε δραστηριότητες, που να ανταποκρίνονται στο γνωστικό επίπεδο των παιδιών και να εναρμονίζονται με τους στόχους που ορίζει το Δ.Ε.Π.Π.Σ. για το Νηπιαγωγείο.
Προτού αναφερθούμε στη παρουσίαση των χαρακτηριστικών του Cabri και των Δραστηριοτήτων, θα κάνουμε μια σύντομη νύξη γύρω από την χρήση του υπολογιστή στη Προσχολική Εκπαίδευση.
ΤΠΕ και Εκπαίδευση
Ο Ηλεκτρονικός Υπολογιστής στη Προσχολική Εκπαίδευση
Ζούμε σε μια εποχή που δε μπορούμε να φανταστούμε τη ζωή μας χωρίς τον ηλεκτρονικό υπολογιστή. Αναπόφευκτα, έχει εισχωρήσει και σε όλες τις βαθμίδες της εκπαίδευσης. Όπως, έχει τονίσει ο Papert o υπολογιστής είναι τόσο σημαντικό εργαλείο για τα παιδιά της τεχνολογικής εποχής, όσο το μολύβι και το χαρτί για τα παιδιά της προηγούμενης γενιάς (Ντολιοπούλου, 1999). Η εισαγωγή του στις προσχολικές τάξεις αποτελεί μία από τις πιο σημαντικές καινοτομίες των τελευταίων ετών στην εκπαίδευση των μικρών παιδιών. Ένα βασικό πλεονέκτημα του υπολογιστή, και πιθανόν ένας από τους λόγους διάδοσής του, είναι η δυνατότητά του να προσφέρει πολλές διαφορετικές εμπειρίες, δίνοντας την ευκαιρία σε παιδιά από διαφορετικά κοινωνικά, οικονομικά κ.α. πλαίσια να αποκτήσουν γνώσεις και να εκφραστούν με πολλαπλούς τρόπους.
Όσον αφορά την αξιοποίηση των νέων τεχνολογιών στην προσχολική εκπαίδευση έχουν γίνει σπουδαιότατες ενέργειες. Ενδεικτικά αναφέρουμε την προσπάθεια να προσεγγιστούν οι φυσικές επιστήμες, η περιβαλλοντική εκπαίδευση και οι νέες τεχνολογίες στην προσχολική και πρώτη σχολική ηλικία σύμφωνα με το εποικοδομητικό μοντέλο μάθησης. Έχουν επίσης ανιχνευτεί θέματα όπως η χρήση υπολογιστών σε νηπιαγωγεία η στάση των νηπιαγωγών απέναντι στην εισαγωγή των υπολογιστών στην πρώτη σχολική ηλικία, η προσέγγιση των φυσικών επιστημών και των μαθηματικών ή η χρήση συστημάτων εικονικής πραγματικότητας με μικρά παιδιά. Μάλιστα όσον αφορά τη στάση των νηπίων τα αποτελέσματα πρόσφατης έρευνας σε μαθητές προσχολικής αγωγής με στόχο «τη διερεύνηση των εμπειριών των νηπίων και τη μελέτη των γνώσεων, δεξιοτήτων, στάσεων και συμπεριφορών που καλλιεργούν οι μαθητές και οι μαθήτριες του νηπιαγωγείου, όταν εμπλέκονται σε μαθησιακές δραστηριότητες με υπολογιστή», έδειξαν ότι η παιδαγωγική αξιοποίηση του υπολογιστή στην εκπαιδευτική διαδικασία είχε θετική επίδραση στην ποιότητα της μάθησης των παιδιών μέσω της ενεργού συμμετοχής τους σε αυθεντικές, βιωματικές μαθησιακές διαδικασίες, καθώς επίσης και ότι ανέπτυξαν και καλλιέργησαν πνευματικές δεξιότητες υψηλού επιπέδου και δεξιότητες σε γνωστικό, συναισθηματικό, και κοινωνικό επίπεδο (Ντολιοπούλου, 2000).
Μαθηματικά και Υπολογιστές
Οι σύγχρονες αντιλήψεις σχετικά με τη διδασκαλία και τη μάθηση των Μαθηματικών, θεωρούν ότι η διδασκαλία των Μαθηματικών δεν αφορά μόνο γνώσεις και κατάκτηση ενός συγκεκριμένου επιπέδου ικανοτήτων, αλλά περιλαμβάνει διαδικασίες μάθησης, οι οποίες αντιμετωπίζουν τα μαθηματικά με μια νέα παιδαγω-διδακτική προσέγγιση, που στηρίζεται στην ερευνητική – ανακαλυπτική διάθεση του μαθητή (Δημητρακοπούλου, 1998). Ο σκοπός της διδασκαλίας των Μαθηματικών εντάσσεται στους γενικότερους σκοπούς της εκπαίδευσης, μεταξύ των οποίων είναι η ολοκλήρωση της προσωπικότητας του μαθητή και η επιτυχής κοινωνική ένταξή του (Δ.Ε.Π.Π.Σ., 2000). Για την επίτευξη των παραπάνω στόχων χρειάζονται συνδυαστικές μέθοδοι διδασκαλίας που θα εξασφαλίζουν την ενεργητική συμμετοχή όλων των μαθητών μέσα στην τάξη ανάλογα με τις δυνατότητές τους. Οι μαθητές θα εργάζονται κριτικά, ανακαλυπτικά, συνεργατικά, δημιουργικά μέσα από ομάδες εργασίας, παράλληλη χρήση Η/Υ και άλλων δραστηριοτήτων. Ο ρόλος του εκπαιδευτικού θα είναι συμβουλευτικός και καθοδηγητικός.
Είναι, πλέον παραδεκτό ότι μια από τις εν δυνάμει καινοτόμες χρήσεις των υπολογιστών είναι και η ανάπτυξη της μαθηματικής παιδείας των μαθητών. Ολοένα και περισσότερο αναγνωρίζεται η σημασία της πληροφορικής ως εργαλείου στη διδασκαλία και τη μάθηση μαθηματικών εννοιών αλλά και όλων των άλλων γνωστικών αντικειμένων. Στην περίπτωση των Μαθηματικών τονίζεται το ότι η Τεχνολογία η οποία διαμορφώνεται και διαμορφώνει τα Μαθηματικά επηρεάζει επίσης και τον τρόπο της διδασκαλίας και της μάθησής τους και δίνει νέες διαστάσεις στο αντικείμενο το οποίο διδάσκεται. Με τη χρήση των υπολογιστών στο σχολείο μπορεί να αλλάξει η κουλτούρα της μάθησης των μαθηματικών κατά τρόπο που δεν κατάφερε η παραδοσιακή διδασκαλία. Βέβαια κάτι τέτοιο δεν σημαίνει ότι καταργούνται τα παραδοσιακά μαθηματικά, αλλά η προσέγγιση μέσω του υπολογιστή τα διευρύνει και τα ζωντανεύει.
Θεωρίες μάθησης
Κοινωνικές και εποικοδομιστικές προσεγγίσεις στη μάθηση
Α) Η σημασία της εμπειρίας του ατόμου στην κατασκευή της γνώσης του
Σύμφωνα με τις σύγχρονες θεωρίες μάθησης, η εμπλοκή του ατόμου στην επίλυση εμπειρικών προβλημάτων θεωρείται βασική κατασκευή της γνώσης του. Η αξία των γνωστικών δομών του ατόμου καθορίζεται από το κατά πόσον αυτές ταιριάζουν με την εμπειρία του και κατά πόσον είναι βιώσιμες, δηλαδή κατά πόσον μπορούν να λύσουν προβλήματα. Για να μπορέσει το άτομο να μάθει μέσα από την εμπειρία του, θα πρέπει να παρατηρήσει και να οργανώσει τα γεγονότα που την αποτελούν χωρίζοντάς τα σε μέρη. Στη συνέχεια, θα πρέπει να ερμηνεύσει την εμπειρία προβλέποντας τα αναμενόμενα αποτελέσματα σε μελλοντικές παρόμοιες καταστάσεις. Εάν μέσα από την οργάνωση αυτή κάποιο συμπέρασμα φανεί χρήσιμο, τότε σημαίνει ότι η οργάνωση αυτή είναι βιώσιμη και το άτομο κατανόησε τον πραγματικό κόσμο.
Στο περιβάλλον Cabri-geometry II οι μαθητές έχουν τη δυνατότητα να πειραματιστούν προκειμένου να πραγματοποιήσουν μια γεωμετρική κατασκευή ή να προβληματιστούν για το τι είναι δυνατόν να συμβαίνει σε ένα γεωμετρικό πρόβλημα και να διατυπώσουν εικασίες- προβλέψεις- γενικεύσεις. Μέσα από την πειραματική διαδικασία ο μαθητής αποκτά σιγουριά για το τι είναι αυτό που συμβαίνει και αποζητά πλέον τρόπους προκειμένου να το αποδείξει. Συνεπώς, στην προσπάθεια τους να αναπτύξουν μεθόδους απόδειξης, είναι δυνατόν να συνδυάσουν την επαγωγική και την παραγωγική μέθοδο στα πλαίσια της καλλιέργειας της γεωμετρικής τους λογικής.
Β) Η σημασία των ενεργειών του ατόμου στη μάθησή του
Η μαθηματική γνώση συνδέεται με τη δυνατότητα κατασκευής νέων αποτελεσμάτων και να δεν περιορίζεται στην ανάκληση πληροφορίας από τη μνήμη του ατόμου. Σύμφωνα με τον Piaget, η μαθηματική γνώση είναι περισσότερο λειτουργική παρά εικονική. Οι λειτουργίες αποτελούν ενέργειες που έχουν εσωτερικευτεί από το άτομο μέσω του αναστοχασμού, μπορούν να αντιστραφούν, είναι αμετάβλητες και αποτελούν μέρος ενός συστήματος λειτουργιών. Για τον Piaget ένα σχήμα (scheme) αποτελείται από τα επαναλαμβανόμενα και γενικεύσιμα χαρακτηριστικά που προέκυψαν από τις ενέργειες του ατόμου. Έτσι λοιπόν, σημασία πρέπει να δίνεται στη διαδικασία και στην προσπάθεια κατασκευής αυτής της υποκειμενικής γνώσης και όχι μόνο στα αποτελέσματα αυτής της διαδικασίας.
Το Cabri-geometry II είναι ένα περιβάλλον το οποίο δεν προσφέρει στο μαθητή γνώση που να στηρίζεται στην πληροφορία, αλλά διαθέτει βασικά γεωμετρικά εργαλεία προκειμένου να κατασκευάσει τη γνώση του ενεργητικά. Ο μαθητής χρησιμοποιώντας τα εργαλεία που προσφέρει το περιβάλλον μπορεί να δημιουργήσει γεωμετρικές κατασκευές. Επιπλέον, ο μικρόκοσμος του Cabri-geometry II, παρέχει στο μαθητή δυνατότητες υψηλής αλληλεπίδρασης καθώς όλες οι ενέργειες του συνοδεύονται από εικονική ανατροφοδότηση ή από λεκτικά μηνύματα. Αυτό συμβαίνει ώστε ο χρήστης να μην αισθάνεται χαμένος στο περιβάλλον ή ξένος μέσα σε αυτό. Σύμφωνα με τον Clements (1989), οι δυνατότητες αυτές μπορούν να δώσουν στο μαθητή ευκαιρίες για «δραστήρια» μάθηση σε σύγκριση μάλιστα, με τα παραδοσιακά αδρανή περιβάλλοντα (χαρτί-μολύβι ή φυσικά αντικείμενα), στα οποία οι ενέργειες του μαθητή δεν συνδέονται με κάποια αποτελέσματα (Κορδάκη, 2001).
Γ) Η σημασία του αναστοχασμού στη μάθηση του
Η λειτουργική γνώση είναι αποτέλεσμα αναστοχασμού ο οποίος παρόλο που δεν είναι παρατηρήσιμος, έχει παρατηρήσιμα αποτελέσματα. Σύμφωνα με τον Locke, αναστοχασμός είναι η ικανότητα του νου να παρατηρεί τις λειτουργίες του και είναι το προαπαιτούμενο στάδιο της ερμηνευτικής διαδικασίας. Η ερμηνευτική διαδικασία έχει ως στόχο να βοηθήσει το άτομο να απαντήσει σε ερωτήματα όπως «τι έγινε;» και «γιατί έγινε;». Ο αναστοχασμός κατά τη διαδικασία της μάθησης είναι απαραίτητος στο μαθητή ώστε να φέρει εις πέρας τη δραστηριότητα, εφόσον μπορεί να την ελέγχει και να την παρακολουθεί, να ξέρει οποιαδήποτε στιγμή τι κάνει και γιατί κάτι είναι σωστό. Η προσπάθεια αναστοχασμού που έχει θετικό αποτέλεσμα, αποτελεί ισχυρό κίνητρο για τον μαθητή και συγκεκριμένα, όταν η επιβράβευση της ορθότητας μιας προσπάθειας προέρχεται από την ικανοποίηση που νιώθει ο ίδιος ο μαθητής για το αποτέλεσμα.
Ο υπολογιστής ίσως είναι το μοναδικό μέσο το οποίο επιτρέπει στο μαθητή να κατασκευάσει γραφικές αναπαραστάσεις, να βλέπει τα αποτελέσματα των κατασκευών του, να τα διαχειρίζεται και να τα τροποποιεί δημιουργώντας πιο έξυπνους και πολύπλοκους σχεδιασμούς. Η εικονική ανατροφοδότηση των ενεργειών του μαθητή στο περιβάλλον του Cabri-geometry II, μπορεί να αποτελέσει πολύ αποδοτικό τρόπο εικονικής επικοινωνίας των μαθηματικών ιδεών των παιδιών. Παράλληλα, η Laborde (1992) επισημαίνει τη σημασία που έχει η αισθητηριακή αντίληψη στη λύση των γεωμετρικών προβλημάτων. Ειδικά στο Cabri-geometry II, η δυνατότητα που δίνει ώστε τα σχήματα να μεταβάλλονται στην οθόνη του υπολογιστή, διατηρώντας τις βασικές τους ιδιότητες, μαζί με την εικονική ανατροφοδότηση, διαμορφώνουν ένα νέο είδος αισθητηριακής αντίληψης. Τέλος, η ανατροφοδότηση εκτός από αισθητηριακή, περιέχει και πληροφορίες που βοηθούν τοι μαθητή να ελέγξει την ορθότητα των υποθέσεων που είχε κάνει αρχικά για τις ιδιότητες των σχημάτων (Κορδάκη, 2001).
Δ) Ο υποκειμενικός χαρακτήρας της γνώσης
Σύμφωνα με πρόσφατες έρευνες, οι μαθητές φαίνεται να μην αφομοιώνουν τις πληροφορίες που δέχονται από τις διδακτικές παρεμβάσεις, αλλά να επεξεργάζονται τις πληροφορίες που τους παρέχονται ξεχωριστά ο κάθε ένας, μέσα από τις δικές τους γνωστικές λειτουργίες. Γι’ αυτό άλλωστε τον λόγο, οι αντιλήψεις και οι γνώσεις που έχει ένα άτομο, διαφέρουν από τις γνώσεις και αντιλήψεις που έχει ένα άλλο άτομο. Επιπλέον, οι αντιλήψεις των μικρών παιδιών έχουν κατασκευαστεί μέσα από διαφορετικές ενέργειες, σε διαφορετικές καταστάσεις και δραστηριότητες και δεν μπορούν να θεωρηθούν μη τελειοποιημένες αντιλήψεις των ενηλίκων. Σύμφωνα με τον Piaget (1970), ο αισθησιοκινητικός αντιληπτικός κόσμος των παιδιών έχει χτιστεί μέσα από τις εμπειρίες τους. Και αυτό είναι ιδιαίτερα εμφανές από τις λέξεις που χρησιμοποιούν τα παιδιά, οι οποίες ναι μεν είναι ίδιες με αυτές των ενηλίκων, ωστόσο «η νοητική διαδικασία η οποία παράγεται στο παιδί με τη βοήθεια της γλώσσας δε συμπίπτει με τις πράξεις που υλοποιούν τη νοητική διαδικασία του ενήλικου κατά την εκφορά της ίδιας λέξης (Vygotsky, 1988). Η αναγνώριση του διαφορετικού τρόπου σκέψης των παιδιών επιδρά και στον τρόπο διδασκαλίας, καθώς ο δάσκαλος πρέπει να διαχωρίσει τα δικά του μαθηματικά από τα μαθηματικά του παιδιού, να μην τα ερμηνεύει μέσα από τις δικές του εμπειρίες αλλά να δίνει σημασία στα μαθηματικά που πράγματι το παιδί κατασκευάζει.
Στο ανοιχτό περιβάλλον του Cabri-geometry II, ο μαθητής έχει στην διάθεσή του ποικιλία εργαλείων, με τα οποία μπορεί να κατασκευάσει τις δικές του στρατηγικές επίλυσης σύμφωνα με τις ιδιαιτερότητές του στην μάθηση. Τέλος, η δυνατότητα μελέτης πολλαπλών μορφών αναπαραστάσεων μιας έννοιας μέσα από εικονικά ή αριθμητικά δεδομένα ή γραφικές αναπαραστάσεις δίνει ευκαιρία στους μαθητές να εκφράσουν τις ιδιαιτερότητές τους στον τρόπο που μαθαίνουν.
Ε) Ο ρόλος των εργαλείων στη νοητική εξέλιξη του μαθητή
Οι Noss&Hoyles (1996) θεώρησαν τους υπολογιστές ως εργαλεία όπως είναι τα σφυριά και τα ψαλίδια, τα οποία μπορούν να αναπαραστήσουν συμβολικά συστήματα και επομένως να μεταφέρουν ψυχολογικά σημεία. Το γεγονός ότι ο μαθητής έχει στην διάθεσή του εργαλεία μέτρησης και σχεδίασης, του δίνει τη δυνατότητα να κάνει γενικεύσεις, να εξάγει συμπεράσματα, να πραγματοποιεί συγκρίσεις μεταξύ των υποθέσεων και των αποτελεσμάτων που προέρχονται από μετρήσεις, όπως και να αναπτύξει το αίσθημα της ανάγκης για αιτιολόγηση. Επιπλέον, η ποικιλία εργαλείων και αναπαραστάσεων δίνει την ευκαιρία για εξατομικευμένη μάθηση καθώς ο μαθητής εργάζεται ανάλογα με τις δυνατότητες αλλά και τις ανάγκες που έχει. Η Laborde υποστηρίζει ότι ο τρόπος που θα υλοποιήσει ο μαθητής τις ενέργειές του στο εκπαιδευτικό λογισμικό, τον περιορίζει αλλά ταυτόχρονα τον υποστηρίζει, στην προσπάθεια του να επιλύσει ένα πρόβλημα. Αυτό έχει ως αποτέλεσμα να επιδρά στη διαμόρφωση των στρατηγικών επίλυσης που κατασκευάζει. Τα εργαλεία παίζουν το ρόλο του διαμεσολαβητή μεταξύ του μαθητή και της μαθηματικής έννοιας. Ακόμη, δεν εξυπηρετούν απλώς τις νοητικές διεργασίες αλλά τις διαμορφώνουν και τις τροποποιούν ενώ ταυτόχρονα επηρεάζουν καθοριστικά τις ενέργειες του χρήστη. Παράλληλα, η δραστηριότητα, τα εργαλεία και οι ενέργειες των ατόμων αλληλοσυνδέονται μέσω των διαμεσολαβητικών νοημάτων και των ατόμων που τα χρησιμοποιούν με μοναδικό τρόπο σε συγκεκριμένες περιπτώσεις.
Ο μαθητής στο περιβάλλον του Cabri-geometry II έχει στην διάθεσή του ποικιλία εργαλείων με τα οποία μπορεί να δημιουργήσει γεωμετρικά σχήματα. Τα εργαλεία αυτά έχουν σχεδιαστεί ώστε να απεικονίζουν τις γεωμετρικές έννοιες με γραφικό τρόπο στην οθόνη του υπολογιστή. Τα σχήματα τα οποία κατασκευάζονται στην οθόνη του υπολογιστή ονομάζονται υπολογιστικά αντικείμενα διότι οι ιδιότητές τους διατηρούνται, ενώ η εικονική τους μορφή μπορεί να μεταβάλλεται ύστερα από διαχείρισή τους από τον χρήστη. Έτσι λοιπόν, τα εργαλεία τα οποία υπάρχουν στην διεπιφάνεια του ψηφιακού αυτού περιβάλλοντος όπως και τα υπολογιστικά αντικείμενα, διαμεσολαβούν μεταξύ των γεωμετρικών εννοιών και του μαθητή, κατά τη διάρκεια της αλληλεπίδρασής του με το πρόγραμμα.
Στ) Η σχέση των σχημάτων και των εννοιών στην ανάπτυξη της γεωμετρικής λογικής
Σύμφωνα με την Mariotti (2001), οι εξωτερικές εικόνες αλληλεπιδρούν με τις εσωτερικές οι οποίες ερμηνεύονται σε εικονικές έννοιες, διότι οι εξωτερικές εικόνες παρέχουν αισθητική παρότρυνση για τις εικονικές έννοιες. Υπάρχει μια σχέση μεταξύ της ανάπτυξης της γεωμετρικής λογικής και των εικόνων που σχεδιάζονται στην οθόνη του υπολογιστή. Στο περιβάλλον χαρτί-μολύβι, υπάρχει συμφωνία για το πόσο χρήσιμη είναι η σχεδίαση ώστε να αναπτυχθεί η γεωμετρική λογική. Τα σχήματα στη γεωμετρία έχουν σύνθετο ρόλο στην παρουσίαση της γεωμετρικής γνώσης καθώς αποτελούν ένα είδος «εικονικών εννοιών» (figural concepts). Το να αναγνωρίζει κανείς την εικονική πληροφορία που περιέχουν τα σχήματα και να μπορεί να τα επεξεργαστεί εικονικά είναι πολύ σημαντικό για την κατάκτηση της γεωμετρικής σκέψης. Η Mariotti (2001), υποστηρίζει ότι η γεωμετρία είναι ένας χώρος όπου οι εικόνες και οι έννοιες πρέπει να βρίσκονται σε πλήρη αλληλεπίδραση. Οι δυνατότητες που έχουν οι ηλεκτρονικοί υπολογιστές να δείχνουν πολλαπλές εικονικές αναπαραστάσεις του ίδιου σχήματος, έχουν αξιοποιηθεί ώστε να δημιουργηθεί κατάλληλο εκπαιδευτικό λογισμικό. Οι εικόνες που δημιουργούνται με τη βοήθεια των μικρόκοσμων, δεν είναι αναπαραστάσεις αισθητηριακού επιπέδου που δεν έχουν να παρουσιάσουν κάτι σημαντικό, αλλά έχουν δική τους εσωτερική λογική η οποία εξαρτάται από τη διαδικασία που τις παράγει και τις εμφανίζει στην οθόνη του υπολογιστή.
Το ανοιχτό λογισμικό Cabri-geometry II, βοηθά στο να αλληλεπιδρά το εικονικό και το εννοιολογικό μέρος της γεωμετρικής λογικής. Η αλληλεπίδραση με τον υπολογιστή πραγματοποιείται με την χρήση εντολών που βρίσκονται στο περιβάλλον διεπαφής του λογισμικού, και οι οποίες αντανακλούν κάθε φορά εννοιολογικό και αισθητηριακό σκοπό ταυτόχρονα. Το σχήμα που εμφανίζεται στην οθόνη του υπολογιστή, αναπαριστά μόνο το ένα μέρος της φύσης του. Η εσωτερική λογική με την οποία ένα σχήμα κατασκευάστηκε, δεν εμφανίζεται άμεσα αλλά μόνο όταν ένα του στοιχείο μετακινείται. Με τη λειτουργία του συρσίματος (dragging) μπορεί να μετακινηθεί ένα στοιχείο της εικόνας, ενώ όλες οι υπονοούμενες γεωμετρικές σχέσεις παραμένουν αμετάβλητες. Έτσι η εικόνα φαίνεται διαφορετική, αλλά οι γεωμετρικές της ιδιότητες διατηρούνται. Με αυτό λοιπόν τον τρόπο, διαφαίνονται οι κρυμμένες γεωμετρικές σχέσεις.
Θεωρία Van Hiele
Τα επίπεδα κατανόησης
Ο P. Van Hiele (1959) κατέληξε στη διατύπωση των πέντε επιπέδων κατανόησης και των φάσεων της μάθησης, που τράβηξαν αμέσως τη προσοχή της παγκόσμιας επιστημονικής κοινότητας. Τα επίπεδα αυτά όσον αφορά τη σχολική γεωμετρία είναι τα εξής:
• Επίπεδο 0 : Οι μαθητές αναγνωρίζουν σχήματα από τη συνολική μορφή τους, σαν μια ολότητα. Μπορούν να τα κατονομάσουν π.χ. ως τρίγωνα, τετράγωνα ή κύβους αλλά δεν μπορούν να διατυπώσουν τις ιδιότητές τους. Για την περιγραφή τους χρησιμοποιούν οπτικά πρότυπα π.χ. ένα σχήμα είναι ορθογώνιο όταν μοιάζει με πόρτα κ.λ.π.
• Επίπεδο 1 : Οι μαθητές μπορούν να αναγνωρίσουν ένα σχήμα από τις ιδιότητές του, π.χ. ένα σχήμα είναι ορθογώνιο γιατί έχει τέσσερις ορθές γωνίες. Μπορούν, επίσης, να αναφέρουν άλλες ιδιότητες των σχημάτων, π.χ. «τα ορθογώνια έχουν ίσες διαγώνιες» ή «ένας ρόμβος έχει τις διαγώνιες κάθετες», αλλά δεν μπορούν να τα ορίσουν τυπικά ή να αποδείξουν τις ιδιότητες.
• Επίπεδο 2 : Οι μαθητές συνδέουν τα σχήματα με βάση τις ιδιότητές τους και τα ταξινομούν σε κατηγορίες, π.χ. "κάθε τετράγωνο είναι ορθογώνιο". Αρχίζουν να κατανοούν το ρόλο του ορισμού. Μπορούν να κάνουν απλούς παραγωγικούς συλλογισμούς αλλά δεν μπορούν να κατανοήσουν ή να συνθέσουν πλήρεις αποδείξεις των ισχυρισμών τους.
• Επίπεδο 3 : Οι μαθητές αναπτύσσουν συλλογισμούς για να αποδείξουν μια πρόταση χρησιμοποιώντας δεδομένα π.χ. πώς το αξίωμα της παραλληλίας συνεπάγεται ότι το άθροισμα γωνιών τριγώνου είναι 180ο. Δεν αναγνωρίζουν όμως την ανάγκη για αυστηρότητα στην απόδειξη και δεν κατανοούν τις σχέσεις μεταξύ διαφόρων αξιωματικών συστημάτων. Στο Λύκειο η μελέτη της Γεωμετρίας ξεκινάει από αυτό το επίπεδο.
• Επίπεδο 4 : Οι μαθητές είναι σε θέση να αναλύσουν διάφορα αξιωματικά συστήματα με μεγάλη αυστηρότητα συγκρίσιμη με την προσέγγιση του Hilbert στη θεμελίωση της γεωμετρίας. Γνωρίζουν την ύπαρξη και άλλων αξιωματικών θεμελιώσεων για την Ευκλείδεια Γεωμετρία εκτός από αυτή του Hilbert. Κατανοούν ιδιότητες όπως η συνέπεια, η ανεξαρτησία και η πληρότητα των αξιωμάτων. Μπορούν για παράδειγμα να συγκρίνουν την Ευκλείδεια και τις μη Ευκλείδειες Γεωμετρίες. Μία μειοψηφία μαθητών φτάνει στο επίπεδο αυτό κατά τη διάρκεια της τριτοβάθμιας εκπαίδευσης. Οι περισσότεροι δεν φτάνουν ποτέ.
Ανοιχτά περιβάλλοντα μάθησης
Το Cabri-geometry II
Χαρακτηριστικά του λογισμικού
Το πρόγραμμα Cabri-geometry II αποτελεί ένα περιβάλλον λογισμικού το οποίο δεν περιορίζεται απλώς στο να υποστηρίξει μια εναλλακτική διδασκαλία με τη χρήση υπολογιστή, αλλά υποστηρίζει την ανάπτυξη μιας διερευνητικής προσέγγισης στη διδασκαλία και στη μάθηση της γεωμετρίας. Αποτελείται από ένα πακέτο ισχυρών και προσεκτικά κατασκευασμένων υπολογιστικών εργαλείων για τη δημιουργία γεωμετρικών δραστηριοτήτων και εφαρμογών, η λειτουργία του οποίου βασίζεται στην αμφίδρομη σχέση με τον χρήστη. Επιτρέπει τόσο την κατασκευή όσο και την μελέτη γεωμετρικών αντικείμένων, δίνοντας με αυτόν τον τρόπο στον μαθητή κίνητρα ώστε να επεκτείνει τις αναζητήσεις του στο χώρο της γεωμετρίας.
Δημιουργήθηκε από τους Jean-Marie Laborde και Frank Bellemain στο Institut d’Informatique et Mathematiques Appliquees de Grenoble (IMAG), ένα ερευνητικό εργαστήριο στο Πανεπιστήμιο Joseph Fourier στη Grenoble της Γαλλίας, σε συνεργασία με το Centre National de la Recherche Scientifique (CNRS). Το πρόγραμμα Cabri ΙΙ προέρχεται από ομάδα επιστημόνων που ανήκουν στο χώρο της πληροφορικής, των μαθηματικών, όπως και της διδακτικής των μαθηματικών, με στόχο να προσφέρει μια νέα και δυναμική προσέγγιση στη μάθηση της γεωμετρίας.
Το πρόγραμμα Cabri διαθέτει βασικά πλεονεκτήματα σε σύγκριση με άλλα προγράμματα διδασκαλίας των μαθηματικών, και συγκεκριμένα της γεωμετρίας. Πρόκειται για ένα πακέτο γεωμετρίας το οποίο διαθέτει στοιχεία υψηλής αλληλεπίδρασης. Αποτελεί δυναμικό περιβάλλον μάθησης καθώς ο χρήστης έχει τη δυνατότητα να μεταβάλλει τις μορφές των σχημάτων όταν ορισμένες ιδιότητές τους παραμένουν αμετάβλητες. Ο δυναμικός χαρακτήρας του περιβάλλοντος αφορά ακόμη και στη δυνατότητα εμφάνισης στην οθόνη του υπολογιστή απειρίας ψηφιακών γραφικών αναπαραστάσεων μιας γεωμετρικής κατασκευής που δημιουργείται από το συνδυασμό απλών στοιχειωδών κατασκευών που υπάρχουν στο περιβάλλον διεπαφής (interface) του μικρόκοσμου (Κορδάκη, 2001). Επιπλέον, ο μαθητής μπορεί εύκολα να διαχειριστεί κάθε γεωμετρικό σχήμα με χρήση του συρσίματος (dragging), το οποίο είναι διαθέσιμο από το πρόγραμμα. Έτσι λοιπόν, μέσω αυτής της άμεσης διαχείρισης, άπειρα σχήματα με κοινές ιδιότητες είναι δυνατόν να απεικονίζονται γραφικά στην οθόνη του υπολογιστή, δίνοντας έτσι, την ευκαιρία στο μαθητή να κατασκευάσει αφηρημένες έννοιες που σχετίζονται με αυτές τις ιδιότητες (Laborde, 2001). Ταυτόχρονα, οι περισσότερες από τις ενέργειες του μαθητή συνοδεύονται από γραφική (εικονική) ψηφιακή ανατροφοδότηση. Ο ρόλος της εικόνας έχει αναφερθεί ως υποστηρικτικός στη δημιουργία νοερών εικόνων οι οποίες θεωρούνται ότι αποτελούν βασικό στοιχείο της νοητικής ανάπτυξης του ατόμου και στο περιβάλλον αυτό βοηθούν στην ανάπτυξη της γεωμετρικής λογικής (Mariotti, 2001).
Επίσης, το Cabri-geometry II αποτελεί ισχυρό εργαλείο τόσο για τον δάσκαλο όσο και για τον μαθητή ή τον ερευνητή, καθώς έχει τη δυνατότητα να καταγράφει βήμα προς βήμα το ιστορικό των ενεργειών του χρήστη, ώστε να βγάλουν συμπεράσματα για την διαδικασία της μάθησης που συντελέστηκε σε αυτό το περιβάλλον. Μια επίσης πολλή σημαντική δυνατότητα του ανοικτού αυτού περιβάλλοντος μάθησης είναι ότι διαθέτει εργαλεία στο μαθητή με σκοπό να μπορεί να επιλύει προβλήματα. Η σημασία της ικανότητας επίλυσης προβλημάτων είναι σημαντική για την ανάπτυξη της μαθηματικής σκέψης των παιδιών.
Σύμφωνα με τους Clements (1989) και Noss&Hoyles (1992), το ανοικτό περιβάλλον Cabri ΙΙ μπορεί να υποστηρίξει τη διεπιστημονική προσέγγιση στη μάθηση της γεωμετρίας, μέσα από το πλαίσιο των συμφραζομένων στο οποίο συντελείται η μάθηση (Κορδάκη, 2001). Ακόμη, ο μαθητής μπορεί να προσεγγίζει γεωμετρικά θέματα με έναν ποιοτικό τρόπο, δηλαδή χωρίς τη χρήση αριθμών. Η δυνατότητα αυτή τον βοηθά αρχικά να προσεγγίσει τις έννοιες ποιοτικά και στη συνέχεια να προχωρήσει σε πιο ποσοτικές προσεγγίσεις.
Τέλος, το περιβάλλον Cabri ΙΙ χωρίς να διαθέτει ένα σύστημα ελέγχου της ορθότητας των απαντήσεων του μαθητή, ωστόσο του παρέχει εργαλεία τα οποία μπορεί να χρησιμοποιήσει για αυτοδιόρθωση. Ένα ακόμη χαρακτηριστικό του είναι ότι δε μένει στατικό, αλλά μπορεί να εξελίσσεται παράλληλα με το χρήστη. Αυτή η εξέλιξη συντελείται μέσα από τη δημιουργία νέων λειτουργιών-εργαλείων (μακροκατασκευών), τα οποία κατασκευάζονται από τον ίδιο τον χρήστη και μπορούν να τοποθετούνται μόνιμα ως νέες δυνατότητες στο ψηφιακό περιβάλλον.
Βασικές δυνατότητες προγράμματος
Το πρόγραμμα Cabri-geometry II δίνει την ευκαιρία προσέγγισης μιας σειράς θεμάτων τα οποία αφορούν τη γεωμετρία. Συγκεκριμένα, βασικά πεδία αναφοράς είναι η αναλυτική και ευκλείδια γεωμετρία, όπως και γεωμετρικοί μετασχηματισμοί σε περιβάλλον υψηλής αλληλεπίδρασης. Ο χρήστης-μαθητής έχει τη δυνατότητα άμεσης κατασκευής σημείων, ευθειών, ευθύγραμμων τμημάτων, τριγώνων, πολυγώνων, κύκλων και άλλων βασικών σχημάτων. Επιπλέον, μπορεί να μεταφέρει, να μεγεθύνει και να περιστρέψει γεωμετρικά σχήματα γύρω από γεωμετρικά κέντρα και προσδιορισμένα σημεία καθώς και ανάκλαση, συμμετρία και αντιστροφή. Παράλληλα, μπορεί εύκολα να κατασκευάσει κωνικά σχήματα, ελλείψεις και υπερβολές. Ακόμη, μπορεί να δημιουργήσει macro για σημαντικές ή συχνά επαναλαμβανόμενες γεωμετρικές κατασκευές.
Ένας καθηγητής μπορεί να καταρτίσει λίστα περιεχομένων, η οποία θα περιλαμβάνει τα θέματα στα οποία επιθυμεί να επικεντρώσει το ενδιαφέρον και την εξάσκηση των μαθητών του. Επίσης, αντικείμενα που χρησιμοποιούνται για τις κατασκευές μπορούν να μετακινηθούν και να αποκρυφτούν για να περιοριστεί η επιβάρυνση της οθόνης. Οι παλέτες των χρωμάτων και των γραμμών διευκολύνουν τη διαφοροποίηση των σχημάτων ενώ το υλικό animation αναδεικνύει τα δυναμικά χαρακτηριστικά των σχημάτων. Τέλος, κατασκευές και maccro μπορούν να αποθηκευτούν στο σκληρό δίσκο ενώ η επιφάνεια εργασίας η οποία αγγίζει το ένα τετραγωνικό μέτρο, επιτρέπει την εκτύπωση επιφάνειας σχεδίου 8 ½ *11 (Κορδάκη, 2001).
Μεθοδολογία -Τeaching Experiment
Προκειμένου να σχεδιάσουμε τις δραστηριότητες μας εξετάσαμε διάφορες μεθοδολογίες. Ύστερα από σκέψη, καταλήξαμε ότι το «διδακτικό πείραμα» (teaching experiment) είναι αυτή που ανταποκρίνεται στις απαιτήσεις τόσο τις δικές μας, αλλά και παράλληλα ταιριάζει στο χαρακτήρα του λογισμικού Cabri. Με τον όρο διδακτικό πείραμα νοείται, η μεθοδολογία που έχουν περιγράψει οι Steffe &Thompson. To κονστρουκτιβιστικό διδακτικό πείραμα είναι μια τεχνική- μεθοδολογία που διερευνά τη γνώση των παιδιών γύρω από τα μαθηματικά και πώς μπορεί αυτή να αποκτηθεί στο πλαίσιο της διδασκαλίας των μαθηματικών (Steffe, 1991). Συγκεκριμένα, στο διδακτικό πείραμα συμμετέχουν ένας ή δύο μαθητές που απασχολούνται από τον δάσκαλο-ερευνητή σε μια σειρά επεισοδίων. Το διδακτικό πείραμα παρέχει ευκαιρίες για διερευνήσεις του σκεπτικού των μαθητών, διαμέσου της οικοδόμησης μοντέλων.
Οι Steffe &Thompson χαρακτήρισαν την όλη διαδικασία ως μία κατά την οποία ο δάσκαλος «συνεχώς ερευνά πιθανά νοήματα που κρύβονται πίσω από τις πράξεις και λόγια των μαθητών», έτσι ώστε οι πράξεις των μαθητών «καθοδηγούν τον εκπαιδευτικό να κατασκευάσει ένα σύστημα αναφοράς στο οποίο ό,τι κάνει ο μαθητής μπορεί να φαντάζει σωστό». Ο δάσκαλος προοδευτικά αναπτύσσει νέες υποθέσεις, προκειμένου να εξηγήσει τους τρόπους, με τους οποίους οι μαθητές λειτουργούν και σχεδιάζει εργασίες που να προκαλούν τη δημιουργικότητα. Έτσι ο ίδιος θα λέγαμε ότι μοιράζεται ανάμεσα στις προσδοκώμενες από τη μια και στις παρατηρούμενες αντιδράσεις των μαθητών από την άλλη (Norton, A, McCloskey, 2008).
Ο ρόλος του δασκάλου περιλαμβάνει το καθορισμό μοντέλων, ενώ παράλληλα σχεδιάζει και θέτει ερωτήματα στους μαθητές με σκοπό να εξετάσει αυτά τα μοντέλα και να προκαλέσει έτσι τη μάθηση. Σε ένα διδακτικό πείραμα ο δάσκαλος-ερευνητής μετατρέπεται από παρατηρητή σε δρώντα, ώστε να οικοδομήσει μοντέλα σχετικά με τις πράξεις και αντιλήψεις του. Καθ’ όλη τη διάρκεια των δραστηριοτήτων επιλέξαμε να λειτουργούμε ως ερευνήτριες-παιδαγωγοί και φροντίσαμε με κατάλληλες ερωτήσεις να προωθήσουμε και να διευκολύνουμε τις αλληλεπιδράσεις των παιδιών με το λογισμικό. Προκειμένου να αξιολογήσουμε τις δραστηριότητες, αποφασίσαμε να μαγνητοφωνήσουμε τα επεισόδια, καθώς η βιντεοσκόπηση δεν ήταν εφικτή.
Οι δραστηριότητες που επιλέξαμε να κάνουμε, έδωσαν τη δυνατότητα στα παιδιά να διερευνήσουν και να αποκτήσουν εμπειρίες με στόχο να κατασκευάσουν κάτι νέο, να διατυπώσουν υποθέσεις και να αναπτύξουν την αναλυτική τους σκέψη και τον έλεγχο των υποθέσεων τους. Εξάλλου, οι ανοιχτές δραστηριότητες και η δυνατότητα που δίνουν στο μαθητή να τις επιλύει με πολλούς τρόπους είναι κάτι αρκετά σημαντικό διότι του επιτρέπει να φανερώσει τις ιδιαιτερότητές του στη μάθηση, να εξωτερικεύσει δηλαδή, τις εσωτερικές του ατομικές διαφορές (Κορδάκη, 2001). Παρακάτω παρουσιάζεται λεπτομερώς η διδακτική παρέμβαση που πραγματοποιήσαμε στο νηπιαγωγείο.
Διδακτική παρέμβαση με το cabri
Επισκεφθήκαμε το 1ο Ολοήμερο Νηπιαγωγείο του Βόλου, με σκοπό να πραγματοποιήσουμε μια διδακτική παρέμβαση με το λογισμικό Cabri-geometry II σε παιδιά προσχολικής ηλικίας. Η παρέμβαση είχε διάρκεια δύο ημέρες, από 45 λεπτά την κάθε φορά. Απασχολήσαμε 2 αγόρια ηλικίας 5 ετών, τα οποία γνώριζαν τις βασικές λειτουργίες του υπολογιστή σε ικανοποιητικό βαθμό (σωστός χειρισμός ποντικιού, χρήση backspace, κλείσιμο παραθύρου από το Χ, αποθήκευση αρχείου, εναλλαγή γλώσσας).
Οργανώσαμε τρεις δραστηριότητες που είχαν ως στόχο αρχικά τη γνωριμία των παιδιών με το Cabri και τον πειραματισμό τους με αυτό, στη συνέχεια την αξιοποίηση των εργαλείων που προσφέρει και τέλος, τη δημιουργία ενός δικού τους έργου μέσω της σύνθεσης γεωμετρικών σχημάτων. Οι δραστηριότητες μας ήταν εστιασμένες στην ανακάλυψη και τον πειραματισμό. Για το λόγο αυτό, δημιουργήσαμε μικρόκοσμο μόνο στη 2η δραστηριότητα, γιατί κυρίως μας ενδιέφερε η εμπλοκή των παιδιών σε ένα άγνωστο, μέχρι τώρα, ψηφιακό περιβάλλον. Παρακάτω παρουσιάζονται αναλυτικά οι δραστηριότητες με τους στόχους και τη πορεία τους.
1η Δραστηριότητα
Ως αφόρμηση της δραστηριότητας επιλέξαμε να διηγηθούμε την ιστορία του «Τριγωνοψαρούλη» του Βαγγέλη Ηλιόπουλου. Στη συνέχεια, ακολούθησε συζήτηση γύρω από τα σχήματα προκειμένου να διαπιστώσουμε το γνωστικό τους επίπεδο αναφορικά με τα σχήματα. Έπειτα, τους ζητήσαμε να βρουν και να αναγνωρίσουν διάφορα σχήματα μέσα στη τάξη και αφού ανακάλυψαν αρκετά από αυτά, προχωρήσαμε στο λογισμικό.
Έτσι λοιπόν, ανοίξαμε το λογισμικό και προτρέψαμε τα παιδιά να «παίξουν» στο περιβάλλον του cabri για να ανακαλύψουν τις δυνατότητες του. Στόχος της δραστηριότητάς μας ήταν να γνωρίσουν τα παιδιά το λογισμικό και να πειραματιστούν με τα εργαλεία που προσφέρει.
Επεισόδιο 1ο
Πρώτος ξεκίνησε ο Άνθιμος (Ν1), ο οποίος πήρε το ποντίκι και δημιούργησε ένα κύκλο, γεγονός που τον εξέπληξε ευχάριστα. Αυτή η ενέργεια, μας έδωσε την ευκαιρία να θέσουμε στα παιδιά ερωτήσεις σχετικά με το πώς μπορεί να δημιουργήσει κανείς σχήματα στο Cabri. Αξίζει να αναφερθεί πως ο τρόπος εκφοράς του λόγου μας προς τα παιδιά ήταν απλός και προσπαθήσαμε να χρησιμοποιήσουμε λέξεις που να είναι γνωστές σε αυτά αλλά συνάμα να καλύπτουν το βασικό λεξιλόγιο που υπάρχει στο Cabri-geometry II (π.χ. «κουμπάκι-εντολή»). Βέβαια όσο περνούσε η ώρα και τα παιδιά εξοικειώνονταν με το λογισμικό χρησιμοποιούσαμε μόνο την μία λέξη, π.χ. «εντολή».
Φ: Τι σχήμα είναι αυτό πάνω στο κουμπάκι;
Ν1: Τρίγωνο.
Εξηγήσαμε στα παιδιά ότι όταν πάνω σε ένα κουμπί-εντολή απεικονίζεται τρίγωνο, κύκλο, τμήμα κοκ τότε αυτό το σχήμα μπορεί κάποιος να δημιουργήσει.
Φ: Πώς καταλαβαίνεις ότι έχεις επιλέξει κάποιο σχήμα;
Ν1: Όταν έχει σχέδιο αυτό κάνει.
Επεισόδιο 2ο
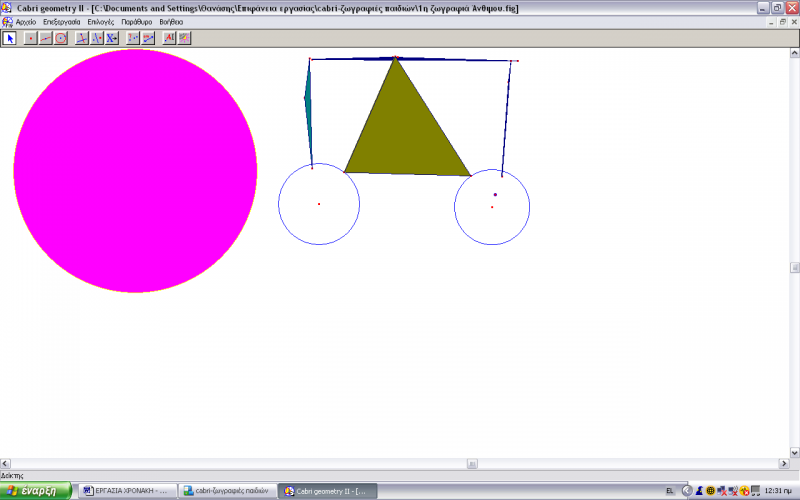
Αφού λοιπόν ο Άνθιμος κατάλαβε τον τρόπο με τον οποίο μπορεί να κατασκευάσει σχήματα πατώντας τα κατάλληλα «πλήκτρα» στην οθόνη του υπολογιστή, δεν έχασε καιρό και άρχισε να δημιουργεί. Μας έκανε ιδιαίτερη εντύπωση το πόσο συγκεντρωμένος, προσεκτικός αλλά και άνετος ήταν καθ’ όλη τη διάρκεια της ενασχόλησης του με αυτό που ανέλαβε να κάνει. Όταν τελείωσε το σχέδιό του, μόνο τότε μίλησε και είπε ότι έκανε ένα βαγόνι.
Ν1: Και τώρα πως θα το χρωματίσω;
Φ: Θα επιλέξεις την εντολή αυτή που δείχνει τον ήλιο (του δείχνει η φοιτήτρια,) και μετά εμφανίζεται ο καμβάς των χρωμάτων.
Ν1: Α, φούξια θέλω!
Και έτσι λοιπόν χρωμάτισε το σχέδιό του.
Επεισόδιο 3ο
Ν1: Θέλω να χρωματίσω το βαγόνι από μέσα.
Ο Άνθιμος, στην περίπτωση αυτή, θέλησε να χρωματίσει τα σχήματα που δημιουργήθηκαν δίπλα από το τρίγωνο. Εξηγήσαμε λοιπόν και στα δύο παιδιά ότι στο Cabri-geometry II μπορεί να χρωματίσει κανείς μόνο όσα είναι σχήματα τα οποία τα έχει επιλέξει μέσα από τις εντολές. Οτιδήποτε είχαν δημιουργήσει με ευθύγραμμα τμήματα και απλά τα ένωναν, δεν μπορούσαν να τα χρωματίσουν.
Επεισόδιο 4ο
Αφού τελείωσε ο Άνθιμος το έργο του, ήρθε η σειρά του Αστέρη (Ν2) να πειραματιστεί με το λογισμικό.
Φ: Τι έκανες εδώ;
Ν2: Ένα δρόμο να πέφτει!!
Ο Αστέρης δημιούργησε μια ευθεία, που ήταν διαγώνια ως προς την επιφάνεια εργασίας του Cabri και η εξήγηση που έδωσε για αυτό που δημιούργησε ήταν αν μη τι άλλο συμβολική.
Επεισόδιο 5ο
Ωστόσο, δεν ικανοποιήθηκε με το αποτέλεσμα και θέλησε να δημιουργήσει ένα νέο φύλλο εργασίας.
Φ: Θέλεις να το σβήσεις;
Ν2 : Όχι, θέλω καινούριο.
Φ: Ωραία, λοιπόν θα πας εκεί που λέει Αρχείο (του δείχνει η φοιτήτρια που πρέπει να κοιτάξει) και θα πατήσεις εκεί που λέει Άνοιγμα.
Και έτσι ο Αστέρης έμαθε να «ανοίγει » κενές σελίδες στο λογισμικό.
Επεισόδιο 6ο
Ο Αστέρης στην προσπάθεια του να κάνει μια ευθεία και μη γνωρίζοντας καλά ακόμα τα εργαλεία του λογισμικού, επιλέγει το τρίγωνο. Παρατηρεί όμως πως όσο μετακινεί και κρατά πατημένο το πλήκτρο του ποντικιού επάνω στο σημείο-γωνία κορυφής του τριγώνου, αυτό αλλάζει συνεχώς μέγεθος, ανάλογα με το που αφήνει το ποντίκι.
Ενώ «παίζει» με το τρίγωνο και παρατηρεί την αλλαγή της μορφής του, καταφέρνει να βάλει τα τρία σημεία του τριγώνου σχεδόν στη ίδια ευθεία.
Επεισόδιο 7ο
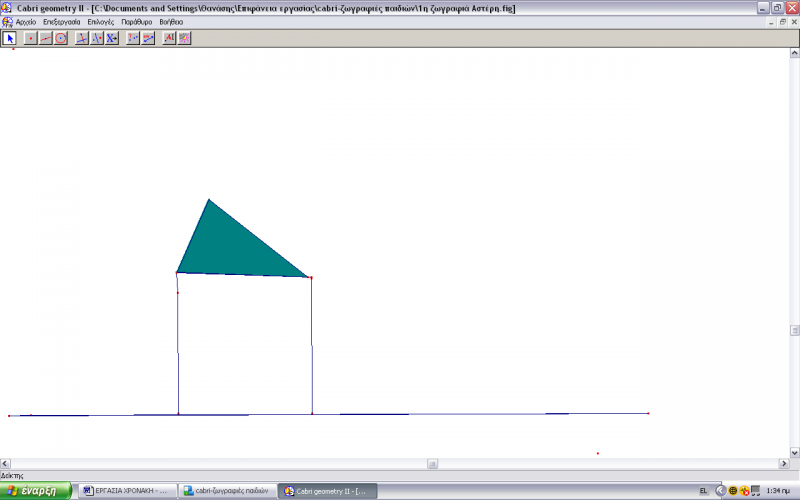
Κατόπιν, μας δηλώνει, ότι θέλει να φτιάξει ένα σπίτι. Ο Αστέρης θα λέγαμε ότι δεν εξοικειώθηκε τόσο γρήγορα, όσο ο Άνθιμος με το λογισμικό και ζήτησε τη βοήθειά μας αρκετές φορές.
Ν2:Θέλω να κάνω ευθεία. Πού θα πάω;
Αφού του λύθηκε η απορία, επέλεξε την εντολή για το ευθύγραμμο τμήμα και έτσι δημιούργησε το κύριο μέρος του σπιτιού, ενώνοντας τα σημεία του ευθύγραμμου τμήματος.
Επεισόδιο 8ο
Ν2: Τώρα θέλω ένα τρίγωνο.
Φ: Θυμάσαι που το είχαμε βρει;
Ο Αστέρης ψάχνει να βρει ποιο κουμπί-εντολή πρέπει να πατήσει για να δημιουργήσει τρίγωνο, προκειμένου να κατασκευάσει τη σκεπή του σπιτιού.
Ν2: Τρι... τρι…Τρίγωνο (Το βρίσκει και το επιλέγει) Το’χω!!!!!
Και με αυτόν τον τρόπο φτιάχνει ένα τρίγωνο το οποίο το ορίζει ως σκεπή του σπιτιού. Στη συνέχεια, θέλησε να χρωματίσει το σχέδιό του αλλά αυτό ήταν ανέφικτό εξαιτίας του ότι ο σκελετός του σπιτιού αποτελούνταν από ευθύγραμμα τμήματα. Γι’ αυτό και χρωμάτισε μόνο τη σκεπή.
2η Δραστηριότητα
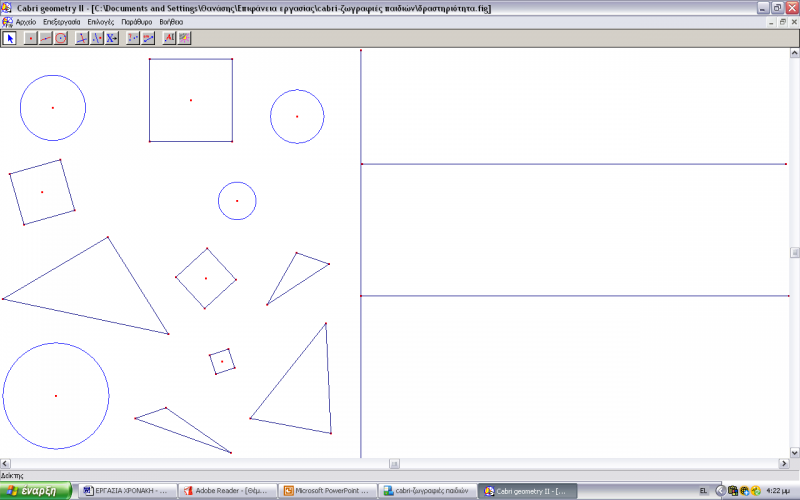
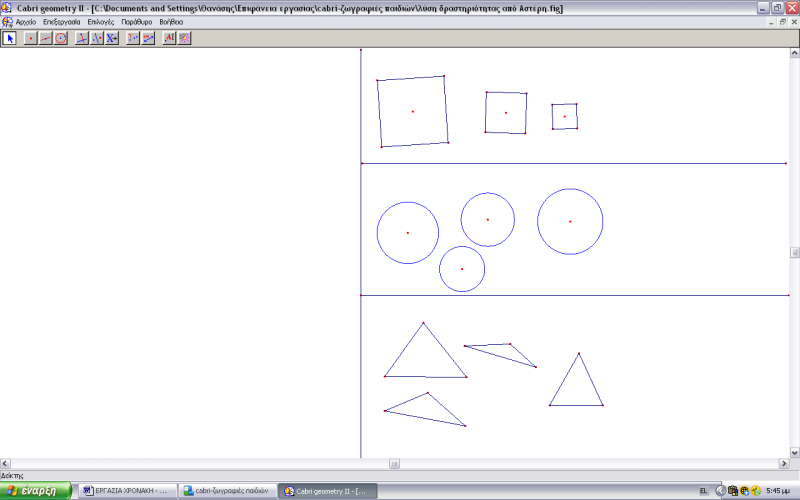
Η δεύτερη δραστηριότητα πραγματοποιήθηκε την δεύτερη ημέρα επίσκεψής μας στο νηπιαγωγείο όπου τα παιδιά είχαν έρθει ήδη σε επαφή με το λογισμικό και είχαν εξοικειωθεί ως ένα βαθμό με αυτό. Στη δραστηριότητα αυτή είχαμε εμείς δημιουργήσει ένα μικρόκοσμο στον οποίο είχαμε τρία είδη σχημάτων-τρίγωνο, κύκλο, τετράγωνο-σε πολλές επαναλήψεις. Στόχος μας ήταν αρχικά να αναγνωρίσουν και να κατονομάσουν τα παιδιά τα σχήματα και κατόπιν να μάθουν τις δυνατότητες του Cabri, όσον αφορά τη μετακίνηση και τη μεταβολή των σχημάτων.
Επεισόδιο 1ο
Φ: Το τετράγωνο γιατί το λέμε τετράγωνο;
Ν2: Γιατί έχει 4 πλευρές.
Ν1:… 4 πλευρές και 4 γωνίες.
Φ:Ο κύκλος έχει πλευρές;
Ν2:Όχι, έχει μόνο γωνίες
Ν1: Δεν έχει γωνίες
Ν2: Τι λες;
Τα παιδιά παρατηρούμε πως έχουν κάποιες γνώσεις για το ποια είναι τα χαρακτηριστικά του κάθε γεωμετρικού σχήματος, αλλά για μερικά από αυτά έχουν παρανοήσεις.
Επεισόδιο 2ο
Η δραστηριότητα αυτή απευθυνόταν και στα δύο νήπια τα οποία παρακολουθούσαν ενώ το ποντίκι το κρατούσε το κάθε παιδί εναλλάξ.
Φ:Τα σχήματα είναι ανακατεμένα. Θα μπορούσες άραγε να τα μετακινήσεις και να τα βάλεις σε ομάδες; Ξεχωριστά τα τρίγωνα, ξεχωριστά τα τετράγωνα, ξεχωριστά τους κύκλους.
Ν1: Αυτό είναι πολύ εύκολο για μένα!
Έτσι λοιπόν, ο Άνθιμος, πήρε το ποντίκι και άρχισε να πειραματίζεται με τις δυνατότητες συρσίματος αλλά και μεταβολής του σχήματος. Οποιαδήποτε κίνηση και να έκανε με το ποντίκι, ανακάλυπτε διαφορετικά πράγματα κάθε φορά.
Επεισόδιο 3ο
Ν2 :Ωχ, γιατί δεν το παίρνει;
Στην περίπτωση αυτή ο Άνθιμος προβληματίστηκε πολύ γιατί ενώ επέλεγε με το ποντίκι το σχήμα, αυτό δεν μετακινούνταν αλλά άλλαζε μέγεθος ή μορφή. Τον αφήσαμε λίγα λεπτά να το ανακαλύψει μόνος και όταν ζήτησε τη βοήθειά μας του εξηγήσαμε.
Φ: Αν παρατηρήσεις στην οθόνη, κάθε φορά που πηγαίνεις με το ποντίκι σου επάνω σε ένα σχήμα, τι εμφανίζεται;
Ν1: Ένα χέρι.
Φ: Όταν κινείς το ποντίκι σου επάνω στο σχήμα, το χέρι αλλάζει;
Ν1: Ναι, γίνεται έτσι (δείχνει το νήπιο με το δικό του χέρι).
Φ: ¨Όταν λοιπόν, το χέρι είναι «έτσι», τότε σημαίνει ότι μπορούμε να το μετακινήσουμε.
Κατάλαβε λοιπόν, τον τρόπο με τον οποίο λειτουργεί η δυνατότητα του συρσίματος σε κάθε σχήμα (μετακίνηση κύκλου από το κέντρο του, μετακίνηση τριγώνου και τετραγώνου από τις πλευρές τους).
Επεισόδιο 4ο
Ν2: Να τα βάλω σε σειρά (σχήματα);
Φ: Βάλε τα όπως θέλεις εσύ.
Ν2: Να τα μικρύνω;
Αφού τελείωσε ο Άνθιμος την πρώτη ομάδα σχημάτων, πήρε το ποντίκι ο Αστέρης και ξεκίνησε την μετακίνηση των σχημάτων. Παρατήρησε όμως, πως ο χώρος που είχαν τα κουτάκια μέσα στα οποία τοποθετούσαν τα σχήματα, δεν έφτανε για να χωρέσουν όλα μέσα. Έτσι λοιπόν, πήρε την πρωτοβουλία να τα μικρύνει. Ήξερε, πλέον, από ποιο σημείο πρέπει να «πιάσει» το σχήμα ώστε να το μικρύνει ή να το μεγαλώσει (μεταβολή μεγέθους κύκλου από το τόξο, μεταβολή μεγέθους τριγώνου και τετραγώνου από τις γωνίες τους).
Επεισόδιο 5ο
Ν2: Ωχ, το έκανα μεγάλο. Θέλω να το σβήσω.
Φ: Θυμάστε πώς σβήνουμε;
Ν2: Πατάς αυτό, πατάς εκεί που θέλεις να το σβήσεις και πατάς αυτό (δείχνει το πλήκτρο backspace).
Τη δυνατότητα του λογισμικού να μπορείς να σβήνεις κάτι που θέλεις, τα παιδιά την ανακάλυψαν την προηγούμενη ημέρα όταν πειραματίζονταν με το Cabri-geometry II και έκαναν σχήματα που δεν τους άρεσαν και ήθελαν να τα σβήσουν. Το αξιοσημείωτο εδώ είναι ότι τους το δείξαμε μία φορά και από τότε ήξεραν πώς να το κάνουν μόνα τους (επιλέγεις την εντολή με το βελάκι, επιλέγεις αυτό που θέλεις να σβήσεις και μετά πατάς Βackspace).
3η Δραστηριότητα
Η δραστηριότητα αυτή είναι και εκείνη η οποία άρεσε περισσότερο στα παιδιά. Στόχος μας ήταν να «παίξουν» με τα εργαλεία του λογισμικού και τα έτοιμα γεωμετρικά σχήματα, για να κάνουν τις δικές τους συνθέσεις. Πρώτος ξεκίνησε ο Άνθιμος και στη συνέχεια ακολούθησε ο Αστέρης.
Επεισόδιο 1ο
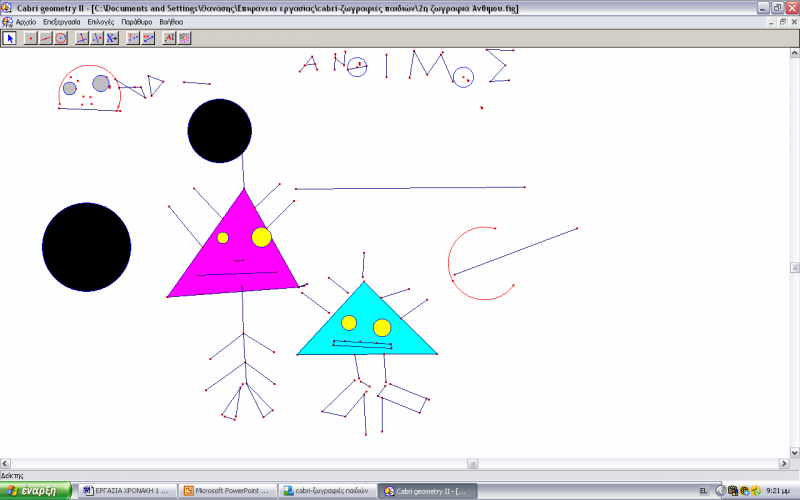
Ο Άνθιμος, έχοντας μάθει και αφομοιώσει τις δυνατότητες που προσφέρει το λογισμικό, όταν του είπαμε να κάνει ο,τι θέλει, πήρε το ποντίκι και άρχισε να σχεδιάζει χωρίς να μιλά. Η συμπεριφορά του όταν σχεδίαζε ήταν η ίδια με αυτή της πρώτης δραστηριότητας. Ήταν απόλυτα προσηλωμένος στην οθόνη του υπολογιστή, επέλεγε με πολλή προσοχή τα εργαλεία που θα χρησιμοποιούσε και γνώριζε τον τρόπο για να διορθώσει τα λάθη του. Εντύπωση μας έκανε η συμπεριφορά του όταν ο Αστέρης τον ρώτησε τι είναι αυτό που σχεδιάζει και εκείνος δεν απάντησε (βλ.εικ5).
Επεισόδιο 2ο
Ο Άνθιμος στο σχέδιό του χρησιμοποίησε βασικά γεωμετρικά σχήματα (κύκλος, τρίγωνο), ευθύγραμμα τμήματα, τόξα και σημεία. Κυρίως χρησιμοποίησε τα ευθύγραμμα τμήματα τα οποία τα ένωνε μεταξύ τους για να σχεδιάσει αυτό που ήθελε. Επιπλέον, έκανε χρήση των δυνατοτήτων του λογισμικού όπως είναι η μετακίνηση και η μεταβολή των σχημάτων.
Ν1: Θέλω να κάνω καμπύλη. Πού θα πάω;
Η φοιτήτρια σε αυτή την περίπτωση του είπε πως θα κάνει μια καμπύλη, μέσω της εντολής «Τόξο». Στη συνέχεια, χρωμάτισε τους κύκλους και τα τρίγωνα και όταν τον ρώτησε για μια ακόμη φορά ο Αστέρης τι έχει φτιάξει, τότε απάντησε πως έφτιαξε εξωγήινους.
Επεισόδιο 3ο
Φ: Θέλεις να γράψεις το όνομα σου;…
Πριν ακόμα η φοιτήτρια ολοκληρώσει την πρότασή της, ο Άνθιμος κρατώντας το ποντίκι έγραψε επάνω στην οθόνη του υπολογιστή το όνομά του. Μας εντυπωσίασε ο τρόπος σκέψης του αλλά και η δημιουργικότητά του. Η φοιτήτρια σε αυτή την περίπτωση είχε στο μυαλό της, τα παιδιά να χρησιμοποιήσουν μια δυνατότητα του Cabri κατά την οποία πληκτρολογούν μια λέξη και αυτή μένει στην οθόνη. Ο Άνθιμος όμως έγραψε το όνομα του με τη βοήθεια των ευθύγραμμων τμημάτων και του κύκλου για το Θ και το Ο.
Επεισόδιο 4ο
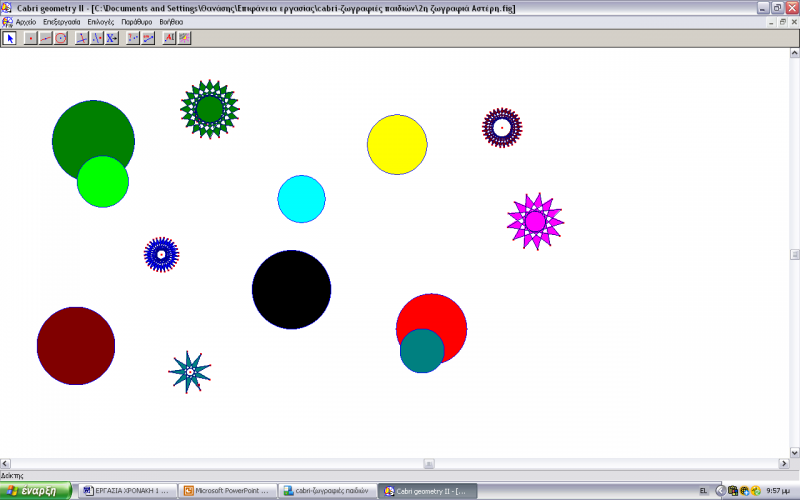
Τελειώνοντας ο Άνθιμος, αναλαμβάνει να σχεδιάσει ο Αστέρης. Το νήπιο αυτό επηρεασμένο προφανώς από το προηγούμενο, δήλωσε εξαρχής πως θέλει να φτιάξει το διάστημα. Έτσι λοιπόν, τα σχήματα που επέλεξε ήταν ο κύκλος και το κανονικό πολύγωνο, το οποίο το χρησιμοποίησε για να κάνει αστέρια. Σε σχέση με το πρώτο αγόρι, ο Αστέρης ήταν ιδιαίτερα ομιλητικός και συνεργάσιμος. Οπουδήποτε και να δυσκολευόταν ζητούσε τη βοήθειά μας και η αλήθεια είναι ότι πειραματίστηκε περισσότερο με τα γεωμετρικά σχήματα από τον Άνθιμο.
Επεισόδιο 5ο
Ν2: Πώς θα κάνω αστέρια;
Ο Αστέρης ήξερε πολύ καλά πώς να κινηθεί για να σχεδιάσει. Ήξερε ότι επιλέγοντας την κατάλληλη εντολή θα έκανε κύκλους τους οποίους θα τους ονόμαζε πλανήτες. Δυσκολεύτηκε όμως στο να ανακαλύψει πώς να κάνει αστέρια. Έτσι λοιπόν, η φοιτήτρια του εξήγησε πως με τη βοήθεια του πολυγώνου θα μπορούσε να τα δημιουργήσει.
Φ: Γιατί το σχήμα αυτό (το πολύγωνο) να λέγεται έτσι;
Ν2: Γιατί έχει πολλές γωνίες.
Φ: Για δες τι μπορείς να κάνεις με αυτό.
Κι έτσι ο Αστέρης πειραματίστηκε με ένα διαφορετικό σχήμα από τα ήδη γνωστά, και με τη βοήθεια των δυνατοτήτων που προσφέρει το λογισμικό, άλλαξε τη μορφή του, το μέγεθός του και τέλος τη θέση του.
Επεισόδιο 6ο
Ν2: Τις βουλίτσες τις βγάζει στην εκτύπωση;
Φ: Θέλεις να το εκτυπώσουμε για να δούμε;
Τα παιδιά όταν έλεγαν βουλίτσες εννοούσαν τα σημεία και επειδή είχαν κόκκινο χρώμα, πολλές φορές τα χρησιμοποίησαν στο σχέδιό τους. Γι΄ αυτό λοιπόν, όταν ήρθε η ώρα να εκτυπώσουν το έργο τους, ήθελαν να ξέρουν αν τα σημεία θα φαίνονται στο χαρτί ή όχι. Τέλος, αφού ο Αστέρης ολοκλήρωσε τα σχήματα που ήθελε να κάνει, τα χρωμάτισε με χρώματα της αρεσκείας του.
Αξιολόγηση της διδακτικής παρέμβασης
Στόχος της πρώτης δραστηριότητας ήταν να γνωρίσουν τα παιδιά το λογισμικό και να πειραματιστούν με τις δυνατότητες που προσφέρει. Ο στόχος επιτεύχθηκε καθώς τα παιδιά έμαθαν να χειρίζονται τα βασικά εργαλεία του Cabri. Ούτως ή άλλως η δραστηριότητα αυτή κινήθηκε σε επίπεδο γνωριμίας και αυτό που ήταν σημαντικό για εμάς ήταν η αντίδραση των παιδιών σε ένα άγνωστο λογισμικό για αυτά. Γι’ αυτό το λόγο επιλέξαμε να μη δημιουργήσουμε μικρόκοσμους, αλλά να αφήσουμε τα παιδιά ελεύθερα να ανακαλύψουν τις δυνατότητες του.
Θα πρέπει να αναφέρουμε πως τα παιδιά γνώριζαν ήδη τα βασικά χαρακτηριστικά των σχημάτων, πράγμα που διευκόλυνε την παρέμβασή μας. Εντύπωση μας έκανε το πόσο γρήγορα και άνετα τα παιδιά κινήθηκαν στο περιβάλλον του Cabri. Αμέσως, προσαρμόστηκαν και άρχισαν να αλληλεπιδρούν με αυτό. Συγκεκριμένα το πρώτο νήπιο, μας εξέπληξε με τη συμπεριφορά του όταν χρησιμοποιούσε το λογισμικό, καθώς έδειχνε την εντύπωση κάποιου που γνωρίζει ακριβώς τι θέλει να κάνει. Τελείωσε το σχέδιο του αρκετά γρήγορα, χωρίς να μας ρωτήσει πολλά πράγματα, γεγονός που μας αιφνιδίασε ευχάριστα. Το δεύτερο νήπιο ήταν πιο συγκαταβατικό κατά την αλληλεπίδραση του με το λογισμικό σε σχέση με το πρώτο. Ζητούσε μεν τη βοήθεια μας συχνότερα, αλλά γρήγορα αφομοίωνε τις καινούριες πληροφορίες. Φροντίσαμε να είμαστε όσο γινόταν δυνατό πιο υποστηρικτικές, ενθαρρυντικές και να αφήσουμε τα παιδιά ν’ ανακαλύψουν ελεύθερα τις δυνατότητες που προσφέρει το Cabri.
Αναφορικά με τη 2η δραστηριότητα θα λέγαμε ότι ο βασικός στόχος μας ήταν να ανακαλύψουν τα παιδιά πώς μπορούν να μετατρέψουν και να μετακινήσουν τα σχήματα. Και αυτός ο στόχος επιτεύχθηκε. Τα παιδιά ενώ «έπαιζαν» με το ποντίκι, συνεχώς ανακάλυπταν νέες λειτουργίες, εμείς δε χρειάστηκε να παρέμβουμε, αφού όλα προέκυπταν αβίαστα. Το μόνο που τα προβλημάτισε, ήταν το πώς θα μεταφέρουν τους κύκλους, καθώς η διαδικασία που έπρεπε να ακολουθήσουν ήταν διαφορετική από αυτή που είχαν χρησιμοποιήσει κατά τη μεταφορά των τριγώνων και τετραγώνων. Όσον αφορά τα σχήματα τα παιδιά αναγνώρισαν τις διαφορετικές αναπαραστάσεις του κάθε σχήματος, πράγμα που διέγειρε τις αναπαραστασιακές ικανότητες τους, δίνοντας τη δυνατότητα να σκέφτονται με διαφορετικό τρόπο και ν’ αναστοχάζονται πάνω σε αυτές (Κορδάκη, 2001). Σε γενικές γραμμές η δραστηριότητα φάνηκε εύκολη στα παιδιά που την ολοκλήρωσαν με επιτυχία σε σύντομο χρονικό διάστημα.
Τέλος, στη 3η δραστηριότητα αφήσαμε τα παιδιά να εκφραστούν δημιουργώντας συνθέσεις γεωμετρικών σχημάτων στο ψηφιακό περιβάλλον του λογισμικού. Αντιληφθήκαμε από τη συμπεριφορά των παιδιών, ότι η συγκεκριμένη δραστηριότητα τους φάνηκε ιδιαίτερα διασκεδαστική, σε σχέση με τις προηγούμενες. Αυτό πιθανώς συνέβη γιατί στη 1η δρασ/τα τα παιδιά δε γνώριζαν το λογισμικό, στη 2η δρασ/τα έπρεπε να κάνουν κάτι συγκεκριμένο, ενώ η 3η ήταν καθαρά ελεύθερη δημιουργία. Ένας άλλος παράγοντας, ενδεχομένως να είναι και ο ψυχολογικός, αφού τα παιδιά είχαν στη τελευταία δρασ/τα μεγαλύτερη αυτοπεποίθηση ως απόρροια της εμπειρίας τους.Κάτι που ακόμη μας έκανε εντύπωση, ήταν η δημιουργικότητα, η φαντασία των δύο παιδιών και οι πρωτότυπες ιδέες τους .
Αποτίμηση της εμπειρίας
Συνοψίζοντας το ανοιχτό λογισμικό δυναμικής γεωμετρίας Cabri-geometry II αποτελεί σημαντικό εργαλείο στα χέρια του εκπαιδευτικού, ο οποίος θέλει να διδάξει γεωμετρία, η οποία μπορεί να είναι εύκολη και ταυτόχρονα δύσκολη. Εύκολη διότι κάποιος μπορεί να «δει» ό,τι λέει, αλλά και δύσκολη διότι πρέπει να έχει κάποιος ιδιαίτερη εξυπνάδα για να λύσει με επιτυχία ένα πρόβλημα (Marrioti, 2001). To Cabri μπορεί να χρησιμοποιηθεί και από παιδιά προσχολικής ηλικίας με μεγάλη επιτυχία και χρήσιμα οφέλη τόσο για τα παιδιά, όσο και για τους εκπαιδευτικούς. Τα αποτελέσματα της παρέμβασης μας ήταν πολύ ενθαρρυντικά, για να συνεχίσουμε να χρησιμοποιούμε την τεχνολογία στο νηπιαγωγείο.
Για να αναπτύξουμε λοιπόν το επίπεδο γεωμετρικής σκέψης των παιδιών προτείνουμε ανεπιφύλακτα την εκμάθηση με τη βοήθεια του λογισμικού της δυναμικής γεωμετρίας Cabri. Πιστεύουμε ότι η πρόωρη επέμβαση με την χρήση της τεχνολογίας μπορεί να παρέχει στους μαθητές τα επαγωγικά εργαλεία που χρειάζονται για να ανεβάσουν το επίπεδο Van Hiele πριν αντιμετωπίζουν τις παραγωγικές αποδείξεις. Σήμερα, οι μαθητές στα σχολεία μεγαλώνουν με τους υπολογιστές και τους βλέπουν γενικά σαν διασκέδαση. Ενώ η Γεωμετρία μπορεί να φαίνεται απόμακρη από τη σκέψη τους αυτοί είναι δεμένοι με τους υπολογιστές. Αυτοί οι μαθητές ίσως να βρουν τη χρησιμοποίηση ενός προγράμματος υπολογιστών στην διδασκαλία της γεωμετρίας σαν μια «ανάσα».
Βιβλιογραφία
Ελληνική
Δημητρακοπούλου Α. (1998), Σχεδιάζοντας εκπαιδευτικά λογισμικά, Σύγχρονη Εκπαίδευση
Κορδάκη, Μ. (2001). Εγχειρίδιο Χρήσης λογισμικού Cabri Geometry II, Καστανιώτης, Αθήνα
Κορδάκη, Μ. (2001). Cabri- Geometry II. Θέματα διδακτικής της γεωμετρίας στο περιβάλλον του εκπαιδευτικού λογισμικού Cabri- geometry II, Καστανιώτη, Αθήνα.
Ντολιοπούλου, Ε. (1999). Σύγχρονες τάσεις της προσχολικής αγωγής, Τυπωθήτω, Αθήνα
ΥΠ.Ε.Π.Θ., (2001), Διαθεματικό Ενιαίο Πλαίσιο Προγραμμάτων Σπουδών για το Νηπιαγωγείο (Δ.Ε.Π.Π.Σ.)
Ξένη
Kordaki, M. & Balomenou A. (2006). Challenging students to view the concept of area in triangles in a broad context: exploiting the features of Cabri-II. International Journal of Computers for Mathematical Learning, Vol. 11, 99-135
Laborde, C., (2001) Integration of technology in the design of geometry tasks with Cabri-geometry. International Journal of Computers for Mathematical Learning. Vol. 6, 283–317,
Mariotti, M. A. (2001). Justifying and proving in the Cabri environment. International Journal of Computers for Mathematical Learning. Vol. 6, 257–281
Norton, A.H. & McCloskey, A., (2008). Teaching experiments and professional development. Journal of Mathematics Teacher Education.1-21
Steffe, P. L., (1991). The constructivist teaching experiment: illustrations and implications. Radical Constructivism in Mathematics Education, E. von Glasersfeld (ed.) 177-194
Van Hiele, P. M. (1986). Structure and Insight: A Theory of Mathematics Education. New York: Academic Press.