Αρίθμηση απο έναν αριθμό και μετά
Submitted by anvoulga on Sat, 06/01/2013 - 23:31
Η παρούσα εργασία με θέμα την «αρίθμηση από έναν αριθμό και μετά» στοχεύει στην πραγματοποίηση από τα παιδιά, αρίθμησης μονάδων ξεκινώντας από άλλο αριθμό πλην του ενός, ενώ ακόμη επιδιώκει να κάνει μια μικρή ανασκόπηση του τι ακριβώς είναι αυτή η μαθηματική έννοια, πως σχετίζεται με άλλες έννοιες, πως αναπτύσσεται στα παιδιά και τέλος πως μπορούμε να διδάξουμε αυτή την έννοια. (παρατίθενται δράσεις που έχουν γίνει καθώς και ένα σενάριο διδασκαλία που προτείνουμε εμείς) Η έννοια αυτή είναι πολύ σημαντική γιατί μόνο αν έχουν προηγηθεί τέτοιου τύπου δραστηριότητες αρίθμησης και τα παιδιά εξοικειωθούν με αυτές, θα προχωρήσουν προς την κατεύθυνση της κατανόησης της πληθυκότητας του αριθμού, και παράλληλα της νοερής αρίθμησης, μέρος της οποίας είναι η μαθηματική έννοια που επεξεργαζόμαστε.
1. Ορισμός της μαθηματικής έννοιας
Ως «αριθμητισμός» (από τον αγγλικό όρο «numeracy») αποδίδεται “η ανάπτυξη αριθμητικών εννοιών και αριθμητικών σχέσεων με τη χρήση συμβάσεων” (αριθμητικά συστήματα, αριθμητικά σύμβολα, μαθηματική ορολογία) (Τζεκάκη 2007, σελ. 201), ενώ ως «αρίθμηση» ή καταμέτρηση (counting) ορίζεται “η απαγγελία μιας σειράς αριθμολέξεων, έτσι ώστε κάθε αριθμολέξη να συνδέεται με μια αριθμήσιμη μονάδα.” (Steffe & Cobb, 1988, στο Καφούση & Σκουµπουρδή σελ 58, 2008) Ωστόσο, ως αρίθμηση, “νοείται η αριθμητική ακολουθία η οποία συμπεριλαμβάνει την ικανότητα αρίθμησης όχι μόνο προς τα εμπρός, αλλά και προς τα πίσω” (Gravenmeijer, 1994 στα πρακτικά του 2ου Πανελλήνιου Εκπαιδευτικού Συνέδριου Ημαθίας). Η «αρίθμηση από έναν αριθμό και μετά» αφορά την αναγνώριση ως αριθμήσιμων μονάδων των αντικειμένων που δεν είναι διαθέσιμα στο ορατό τους πεδίο, και την αρίθμηση επομένως μιας συλλογής αντικειμένων που ένα μέρος της δεν είναι ορατό.
Ο Steffe et al. (1983. 1988, στο Καφούση & Σκουμπουρδή σελ 78, 2008) διέκριναν πέντε τύπους αριθμήσιμων μονάδων που τα παιδιά κατασκευάζουν, όταν αριθμούν για να βρουν την πληθικότητα μιας συλλογής:
1. Αντιληπτικές (perceptual)
2. Αναπαραστατικές (figural)
3. Κινητικές (motor)
4. Λεκτικές (verbal)
5. Αφηρημένες (abstract)
Η εργασία μας θα εστιάσει στο τελευταίο τύπο αριθμητικών μονάδων, τις αφηρημένες, καθώς σε αυτό τον τύπο αρίθμησης, εντάσσεται η αρίθμηση από έναν αριθμό και μετά. Πιο συγκεκριμένα, στο στάδιο αυτό κάθε αριθμολέξη αντιπροσωπεύει και όλες όσες προηγούνται. Για παράδειγμα αν έχουμε κουτιά που μέσα έχουν 3 κρυμμένα αντικείμενα, και είναι τοποθετημένα μπροστά σε ένα παιδί και το ρωτήσουμε πόσα είναι όλα μαζί, τότε μπορεί να φτάσει στο αποτέλεσμα αριθμώντας «3, 4, 5, 6. 7», κάτι που μας δείχνει ότι ξεκινώντας την αρίθμηση από το 3 δεν έχει ανάγκη να μετρήσει τις μονάδες που φτιάχνουν το συγκεκριμένο αριθμό. Σιγά σιγά το παιδί περνά από το συγκεκριμένο στο αφηρημένο, και τελικά πολύ αργότερα θα επιτύχει την νοερή αρίθμηση.
Από τη σχετικά περιορισμένη βιβλιογραφική ανασκόπηση που κάναμε βρήκαμεδύο δράσεις με παιδαγωγικό υλικό, προσαρμοσμένο στη μαθηματική έννοια που εξετάζουμε. Η πρώτη δράση αναφέρεται στο βιβλίο του Van de Walle (2007) και αφορά τρεις διαδοχικές δραστηριότητες, με τις οποίες τα παιδιά εξοικειώνονται και εξασκούνται στην αρίθμηση από ένα αριθμό και μετά. (σελ 183) Η εν λόγω δράση ξεκινά με ένα παιχνίδι στο οποίο τα παιδιά καλούνται να μετρήσουν προς τα μπρός και προς τα πίσω. Όπως ο ίδιος αναφέρει η «απαρίθμηση προς ένα αριθμό- στόχο και αντίστροφα είναι σημαντική άσκηση απαρίθμησης» γιατί βοηθάει τα παιδιά «να αποκτήσουν ευχέρεια με τις αριθμητικές λέξεις τόσο κανονικά όσο και αντίστροφα» και να αριθμούν ξεκινώντας από άλλους αριθμούς εκτός από το ένα. Ακόμη και ίδιος αναγνωρίζει τη δυσκολία της δραστηριότητας, ωστόσο αντιπαραβάλλει σε αυτό, το γεγονός πως τα παιδιά διασκεδάζουν πολύ με αυτή τη δραστηριότητα. Πιο συγκεκριμένα, σε αυτή τη δραστηριότητα πέντε παιδιά τοποθετούνται στη σειρά και από πίσω τους τοποθετούνται 5 καρέκλες. Η τάξη ξεκινά να αριθμεί από το 1-5 και τα παιδιά κάθονται ένα- ένα στις καρέκλες. Όταν φτάσουν στον αριθμό στόχο(5) τότε αρχίζουν να μετρούν αντίστροφα 5, 4, 3.. και το παιδί που κάθισε με το 5, τώρα σηκώνεται όρθιο και ακολουθούν τα υπόλοιπα ένα- ένα με το άκουσμα των αριθμών. Στη συνέχεια, προτείνει μια δεύτερη δραστηριότητα στην οποία δίνονται 10- 12 πούλια σε κάθε παιδί και τους ζητείται να τα βάλουν από αριστερά στα δεξιά πάνω σε μια επιφάνεια και αφού μετρήσουν τέσσερα να τα κρύψουν με την αριστερή παλάμη τους. Έπειτα, ο εκπαιδευτικός λέει: «Δείξτε την παλάμη σας. Πόσα υπάρχουν εκεί; (τέσσερα) Ας μετρήσουμε λοιπόν, έτσι: τ- ε- σ- σ- ε- ρ- α (δείχνοντας την παλάμη τους) πέντε, έξι… δέκα.» (σελ 183) Η διαδικασία επαναλαμβάνεται και με άλλους αριθμούς.
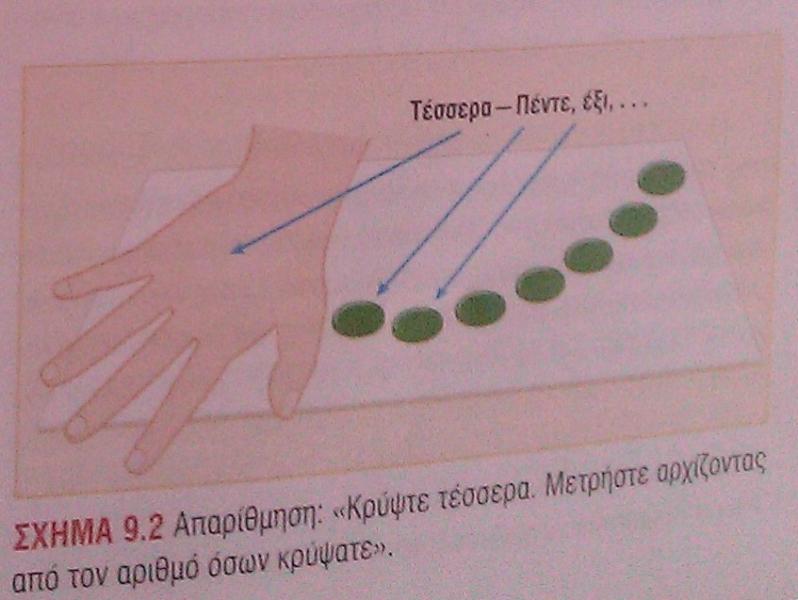
Η τρίτη δραστηριότητα δυσκολεύει περισσότερο τα παιδιά, αφού τώρα καλούνται να επιλύσουν ένα πρόβλημα. Συγκεκριμένα, όπως και στη 2η δραστηριότητα έτσι και εδώ χρησιμοποιείται χειραπτικό υλικό όπως ποτήρι, ζάρι, πούλια και κάρτες με αριθμούς. Ο πρώτος παίχτης παίρνει από τη στοίβα μια κάρτα και τοποθετεί μέσα στο ποτήρι τόσα πούλια όσα υποδεικνύει ο αριθμός της κάρτας. Η κάρτα βρίσκεται δίπλα στο ποτήρι για να θυμόνται τα παιδιά πόσα πούλια έχει μέσα το ποτήρι και ο 2ος παίχτης ρίχνει το ζάρι, τοποθετώντας τα ανάλογα πούλια δίπλα του. Οι παίχτες αποφασίζουν μαζί πόσα πούλια υπάρχουν συνολικά. Επιπρόσθετα, δίνεται η δυνατότητα να φτιαχτεί ένα φύλλο εργασίας- αναφοράς με τρεις στήλες: «μέσα στο ποτήρι», «δίπλα στο ποτήρι», «όλα», το οποίο συμπληρώνεται από τα παιδιά.

Η δεύτερη δράση αναφέρεται στο βιβλίο της Καφούση και Σκουμπούρδη και αφορά ένα πειραματικό πρόγραμμα μαθηματικών στο νηπιαγωγείο, με δραστηριότητες για πολλές μαθηματικές έννοιες. Οι δραστηριότητες έχουν σχεδιαστεί σύμφωνα με το κοινωνικό- πολιτισμικό πλαίσιο της Ρόδου και σε αυτές η νηπιαγωγός εμψυχώνει δύο κούκλες- την Υπατία και τον Ευκλείδη- με τις οποίες πραγματοποιούνται οι δραστηριότητες. Εμείς επιλέξαμε ένα μέρος αυτού του σεναρίου, που περιέχει 3 δραστηριότητες που αφορούν το θέμα «αρίθμηση από έναν αριθμό και μετά». Πιο συγκεκριμένα η δράση ξεκίνα με την εμπλοκή των παιδιών σε ένα πάρκο. Τα παιδιά καλόυνται, ύστερα από προτροπή της Υπατίας και του Ευκλείδη να απαριθμήσουν τις στρουθοκαμίλους και τις διάφορες ομάδες ζώων. (Ποιος αριθμός είναι μετά το 9; Ποιος αριθμός είναι πριν το 7; κ.α) Αφόυ λοιπόν απαριθμήσουν τις δίαφορες κατηγορίες ζώων όπως είναι οι πάπιες, τα ελάφια και οι στροθοκάμιλοι τους ζητήται να βάλουν στην σειρά τις εικόνες από τα λιγότερα προς τα περισσότερα ζώα. Μετά χωρίζουμε τις εικόνες ανα δύο. Και τα παιδία πρέπει να βρούν πόσα ζώα πρέπει να έρθουν ακόμα στην εικόνα με τα λιγότερα ζώα, για να γίνουν τόσα οσα στην εικόνα με τα περισσότερα. (π.χ 3 ελάφια και 5 πάπιες. Λείπουν άλλα δυο ζώα από την πρώτη είκονα για να έιναι ο αριθμός ίσος με την δέυτερη εικόνα. Στην δέυτερη δραστηριότητα τα παιδιά χωρίζονται σε ομάδες όπου τους μοιράζεται μια εικόνα με αντικέιμενα από το πάρκο και τα παιδιά καλούνται να κυκλώσουν την τιμή του αντικείμενου που ανέρχεται σε 6 ή 7 ή 8 ή 9 ή 10 ευρώ αντίστοιχα.
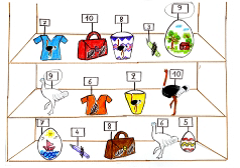
Η τρίτη δραστηριότητα αφορά κυρίως την αρίθμηση από έναν αριθμό και μετά και δυσκολεύει ακόμη περισσότερο τα παιδιά. Ο χώρος δράσης συνεχίζει να είναι το πάρκο. Τα παιδιά τώρα βρίσκονται στο χώρο όπου ζουν τα αλογάκια. Με την παρότρυνση των δύο ηρώων όπου ρωτάνε τα παιδιά πόσα είναι τα αλογάκια αυτά ξεκινούν να τα μετρήσουν. (4 αλογάκια βρίσκονται έξω από τον στάβλο και 2 μέσα). Ελάτε να μετρήσουμε πόσα είναι όλα μαζί; Τα παιδιά αρχίζουν να μετρούν και εξηγούν την λύση τους. Επιβεβαιώνουν την λύση τους απαριθμώντας όλα τα αλογάκια. Η δραστηριότητα επαναλαμβάνεται και με τις υπόλοιπες κατηγορίες ζώων. Όπως είναι τα παπάκια (5 παπάκια βρίσκονται στην λίμνη και 3 μέσα στο σπίτι τους. Πόσα είναι όλα μαζί; Για τα κατσικάκια (6 βρίσκονται έξω από τον στάβλο τους. Αν τα 3 κατσικάκια πάνε μέσα στον στάβλο τους πόσα θα μείνουν;)

Κατά την παρουσίαση των δυο δράσεων προκύπτουν κάποιες ομοιότητες και διαφορές. Πιο συγκεκριμένα παρατηρούμε ότι και στις δύο δράσεις προηγείται μια δραστηριότητα που τους εξοικειώνει με το μέτρημα από άλλο αριθμό εκτός του ένα. Επιπλέον και στις δύο κεντρική είναι η σκέψη πως κρύβουμε κάποια ορατά αντικείμενα, τα οποία έχουμε είτε μετρήσει είτε μας έχει δοθεί ο αριθμός του συνόλου του. Συμπερασματικά προκύπτει η εξής ομοιότητα: Έχοντας απαριθμήσει και κρύψει τα ορατά αντικείμενα συνδέουν το συνολικό αριθμό με την πληθικότητα πχ το 6 δεν είναι απλώς ένας αριθμός αλλά αντιστοιχεί σε 6 αντικείμενα ή στοιχεία. Ενδέχεται με την πρώτη φόρα που θα γίνουν οι δραστηριότητες να μην πετύχουν αυτή τη σύνδεση τα παιδιά. (λύση με αναπαριστάμενες μονάδες μέτρησης, χρήση λεκτικών αριθμήσιμων μονάδων ή αναφορά μόνο βασικού αποτελέσματος) Όμως με την επανάληψη των δραστηριοτήτων τελικά αυτή θα επιτευχθεί και τα παιδιά θα μετρούν από εκείνο το σημείο και μετά, έχοντας νοερά στο μυαλό τους 6 αντικείμενα. Οι διαφορές είναι πιο γενικές όπως ότι η 2η δράση ξεκινά με πιο γενική δραστηριότητα: απαρίθμηση παπάκια στρουθοκαμήλους, ελάφια και συγκρίσεις, κάτι που κατά την γνώμη μας είναι απαραίτητο για να εισαχθούν σταδιακά και εξελικτικά τα παιδιά στη νέα μαθηματική έννοια, «πατώντας» στις κατεκτημένες γνώσεις τους. Άλλη διαφορά είναι ότι η 1η δράση αφορά κυρίως προβλήματα μαθηματικά που περιλαμβάνουν και φύλλο εργασίας.
Ταυτότητα σεναρίου- σχεδίου εργασίας
Τίτλος δραστηριότητας: Κρύψε και Μέτρα
Εμπλεκόμενες γνωστικές περιοχές: Ενότητα: Παιδί και Μαθηματικά:
Το συγκεκριμένο κεφάλαιο εντάσσεται στην ενότητα του Νέου αναλυτικού προγράμματος «Αριθμοί και Πράξεις» και αντιστοιχεί στο γενικό στόχο «Καταμετρούν πραγματικά αντικείμενα και αντικείμενα σε εικόνες και άλλες μορφές συμβολικών παραστάσεων μέχρι το 10.» Αυτός ο στόχος εμπεριέχει την δεξιότητα να αριθμούν τα παιδιά από έναν αριθμό και μετά, κρύβοντας ένα μέρος της ορατής συλλογής και συνεχίζοντας την απαρίθμηση από εκεί και ύστερα. Με αυτό τον τρόπο εισάγονται στην νοερή αρίθμηση, αφού για να πετύχουν τα παραπάνω πρέπει να συγκρατούν στο μυαλό τους τον αριθμό της μη ορατής συλλογής.
Σκοπός και στόχοι του σεναρίου- σχεδίου διδασκαλίας
Γενικός σκοπός: Οι μαθητές να μάθουν σταδιακά να απαριθμούν από έναν αριθμό και μετά, περνώντας από απλές δραστηριότητες αρίθμησης σε δραστηριότητες στις οποίες κρύβεται ένα μέρος της συλλογής των αντικειμένων και συνεχίζουν την απαρίθμηση από εκεί και μετά.
Επιμέρους στόχοι δραστηριοτήτων:
Δ1: Να απαριθμήσουν τον αριθμό των κουμπιών της εικόνας και να χρωματίσουν τον αντίστοιχο αριθμό κύκλων, αναγράφοντας με όποιο τρόπο μπορούν τον αριθμό αυτό. (με σύμβολα, με γραμμές, με τελείες)
Δ2: Να απαριθμήσουν το σύνολο των κουμπιών, από το αριθμό που έχει κρύψει η νηπιαγωγός και μετά.
Δ3: 1. Να αριθμήσουν τον αριθμό των κουμπιών και να τα τοποθετήσουν μέσα στο κουτί, αναγράφοντας με όποιο τρόπο μπορούν τον αριθμό αυτό σε ένα χαρτί. Έπειτα αφού ρίξουν το ζάρι να τοποθετήσουν τον αντίστοιχο αριθμό κουμπιών δίπλα στο κουτί. Να ξεκινήσουν την απαρίθμηση από τον συνολικό αριθμό των κουμπιών μέσα στο κουτί για να βρουν το σύνολο των κουμπιών μέσα και δίπλα στο κουτί, αποφεύγοντας να μετρήσουν πάλι εκείνα που βρίσκονται μέσα στο κουτί. 2. Να αναπτύξουν διαδικασίες δοκιμής, βάζοντας έναν διαφορετικό αριθμό κουμπιών κάθε φορά μέσα στο κουτί ή ρίχνοντας το ζάρι και της επαλήθευσης και ελέγχου του συνολικού αριθμού κουμπιών από την καταμέτρηση που έκαναν.
[b]Εκπαιδευτική μέθοδος: [/b]Ομαδοσυνεργατική και καθοδηγητική μάθηση
Εκπαιδευτικές τεχνικές: Ερωτήσεις- απαντήσεις, Παιχνίδι δομημένο, Ομαδική εργασία, Ατομικό φύλλο εργασίας
Αριθμός παιδιών της τάξης και ηλικία παιδιών: Ο αριθμός των παιδιών είναι 10, ηλικίας 4 έως 6 ετών.
Εκτιμώμενη διάρκεια: Η διάρκεια του σχεδίου είναι 45 λεπτά.
Ανάπτυξη σεναρίου- σχεδίου εργασίας, Γενική περιγραφή
Η Αρίθμηση από έναν αριθμό και μετά
Βασικός στόχος του διδακτικού σχεδίου είναι η κατανόηση της αρίθμησης από έναν αριθμό και μετά στην οποία ενσωματώνονται πέντε συστατικά:
1. Προφορική ονομασία αριθμών
2. Γραπτή ονομασία αριθμών
3. Κατανόηση αφηρημένων αριθμητικών μονάδων (Steffe et al., 1983. 1988, στο Καφούση & Σκουμπουρδή 2008: σελ. 78)
4. Απαγγελία μιας σειράς αριθμολέξεων
5. Κατανόηση της πληθυκότητας του αριθμού( Van de Walle, 2007, σελ. 181)
Σύμφωνα με τον Van de Valle (2006, σελ 260) η απαρίθμηση είναι μια δραστηριότητα κλειδί με την οποία τα παιδιά μπορούν να οικοδομήσουν και να ενσωματώσουν τις πέντε αυτές ιδέες.
Για την κατανόηση της αρίθμησης από έναν αριθμό και μετά χρησιμοποιείται αφενός η συμβολική αναπαράσταση - μοντέλο των κουμπιών και αφετέρου το μοντέλο της «απόκρυψης». (Κρύβω μια ποσότητα κουμπιών και μετρώ από εκεί και πέρα)
Προαπαιτούμενη Γνώση:
Κατά την διδασκαλία του συγκεκριμένου σχεδίου διδασκαλίας οι μαθητές απαιτείται να είναι εξοικειωμένοι με την απαρίθμηση
Περιγραφή δραστηριοτήτων:
Δραστηριότητα 1η
Βήμα 1ο: Η νηπιαγωγός μαζί με τα παιδιά βρίσκεται στην γωνιά των μαθηματικών. Έχει φέρει μαζί της το κουτί της τάξης, το οποίο χρησιμοποιούν πολύ συχνά σε δραστηριότητες τους. Αυτή τη φορά το κουτί περιέχει μέσα πολύχρωμα κουμπιά. Θέλοντας να εισάγει τα παιδιά στην αρίθμηση από έναν αριθμό και μετά, πραγματοποιούν μια δραστηριότητα καταμέτρησης που στηρίζεται στις προηγούμενες γνώσεις των παιδιών.
Βήμα 2ο: τα παιδιά σε δυάδες καλούνται να μετρήσουν μια σειρά κουμπιών μέχρι να φτάσουν στο 10. [Η νηπιαγωγός ενδεικτικά δίνει τέτοιου τύπου καθοδηγήσεις και ερωτήσεις βοηθητικές: «Μετρήστε μου τόσα κουμπιά όσα χρειάζονται για να έχουμε συνολικά 10» «Γιαννάκη είσαι σίγουρος πως αυτά είναι 10;;»(ο Γιαννάκης έχει μετρήσει 9 κουμπιά ως δέκα, μετρώντας 2 φορές το ίδιο αντικείμενο)]
Βήμα 3ο: Η νηπιαγωγός μοιράζει στα παιδιά ατομικά φύλλα εργασίας τα οποία καλούνται τα παιδιά να συμπληρώσουν. Τα φύλλα εργασίας περιλαμβάνουν στην μια στήλη εικόνες από διάφορες ποσότητες κουμπιών, ενώ στην άλλη υπάρχουν κύκλοι. Τα παιδιά πρέπει να χρωματίσουν τόσους κύκλους όσους υποδεικνύει ο αριθμός των κουμπιών και έπειτα να αναγράψουν με όποιο τρόπο μπορούν τον εκάστοτε αριθμό κουμπιών.
Δραστηριότητα 2η
Στη 2η δραστηριότητα τα παιδιά χωρίζονται σε ομάδες 2 ατόμων και δίνονται 10 κουμπιά σε κάθε ομάδα. Το ένα μέλος αποφασίζει πόσα κουμπιά θα κρύψει, και καλύπτει με το χέρι του ένα αριθμό κουμπιών πχ 4, και το δεύτερο μέλος πρέπει να απαριθμήσει από το τέσσερα και μετά. Οι ρόλοι αντιστρέφονται όσες φορές η άσκηση προσελκύει το ενδιαφέρον των παιδιών. (το πολύ 3 φορές) [ενδεικτικές ερωτήσεις νηπιαγωγού: «Πως μπορείς να ελέγξεις αν ο αριθμός που λες είναι σωστός; Και μένα μου φαινόταν δύσκολο στην αρχή να μετρήσω από το πέντε και μετά.» «Τι νομίζεις ότι θα συμβεί αν μετρήσω από το ένα και όχι από το τέσσερα;» «Θα έχω το σωστό αποτέλεσμα;;»]
Δραστηριότητα 3η
Βήμα 1ο: Τα παιδιά χωρίζονται σε 2 ομάδες των πέντε ατόμων προκειμένου να παίξουν ένα παιχνίδι. Το παιχνίδι λέγεται «Κρύψε- μέτρα- προχώρα». Περιέχει ένα ταμπλό, πιόνια, ζάρι, κουτί, φύλλο εργασίας, χαρτάκια. Σκοπός του είναι μια εκ των 2 ομάδων να φτάσει στο τέλος του ταμπλό πιο γρήγορα, πραγματοποιώντας μια σειρά από αριθμήσεις. (η ομάδα που θα φτάσει 1η νικάει) Το παιχνίδι ξεκινά ως εξής: Το πρώτο μέλος της ομάδας τοποθετεί μέσα στο κουτί που- αναφέρθηκε πιο πάνω- έναν αριθμό κουμπιών που επιθυμεί και έπειτα γράφει σε ένα χαρτάκι με όποιον τρόπο μπορεί αυτόν τον αριθμό για να θυμούνται πόσα κουμπιά περιέχει το κουτί. Το δεύτερο μέλος ρίχνει ένα ζάρι και ανάλογα τον αριθμό που θα φέρει τοποθετεί ανάλογο αριθμό κουμπιών δίπλα από το κουτί. Το τρίτο μέλος καλείται να απαριθμήσει το σύνολο των κουμπιών μέσα και δίπλα από το κουτί, ξεκινώντας όμως από τον συνολικό αριθμό των κουμπιών που δεν είναι ορατά (μέσα στο κουτί) και συνεχίζει απαριθμώντας τα υπόλοιπα κουμπιά. Το τέταρτο μέλος κατά την διάρκεια του παιχνιδιού συμπληρώνει ένα φύλλο εργασίας που έχει τις επιλογές: «μέσα στο κουτί» «δίπλα στο κουτί» «όλα». Γράφει τους αντίστοιχους αριθμούς ποσοτήτων των κουμπιών στις επιλογές που τους δίνονται.
Βήμα 2ο: Τέλος, το πέμπτο μέλος της ομάδας κουνάει το πιόνι στο ταμπλό τόσες θέσεις κάθε φορά, όσες υποδεικνύει ο αριθμός της στήλης «ΌΛΑ». Η ομάδα που φτάνει στο τέλος πρώτη νικά!
[ενδεικτικές ερωτήσεις νηπιαγωγού: «πως κατάλαβες ότι το σύνολο των πουλιών είναι 8;;» «Συμβουλεύσου το χαρτάκι δίπλα από το κουτί. Και μέτρα από την αρχή. Πόσα βρήκες τώρα;;» «Είσαι σίγουρος πως μετά το έξι είναι το οκτώ;; Μέτρα μου από το ένα ως το οκτώ για να σιγουρευτείς.»]
Υλικοτεχνική υποδομή: Κουμπιά, κουτί, φύλλα εργασίας, μαρκαδόροι, χαρτάκια, ταμπλό παιχνιδιού, πιόνια, ζάρι.
Αξιολόγηση:
Η αξιολόγηση του συγκεκριμένου σεναρίου γίνεται σε δύο επίπεδα, πρώτον όσον αφορά τους στόχους- μέσα από μια δραστηριότητα- και δεύτερον όσον αφορά τις επιλογές δραστηριοτήτων, στόχων και υλικών που έγιναν. Πραγματοποιώντας αυτήν την αξιολόγηση δίνουμε μια ουσιαστική απάντηση στο αν πέτυχε η δράση που προτείναμε.
Όσον αφορά την δραστηριότητα αξιολόγησης, η νηπιαγωγός θα δώσει στα παιδιά ένα φύλλο εργασίας. Στο συγκεκριμένο, υπάρχουν δύο στήλες, όπου στη πρώτη στήλη βρίσκεται ένα κουτάκι με αριθμό και δίπλα του καραμέλες ενώ η δεύτερη είναι κενή. Ο αριθμός στο κουτί αντιπροσωπεύει μια ποσότητα καραμελών που υποθετικά βρίσκονται μέσα, και δεν είναι ορατές. Τα παιδιά καλούνται να μετρήσουν τις καραμέλες μέσα και δίπλα στο κουτί και συμπληρώνουν τον αντίστοιχο αριθμό στη κενή στήλη. (με συμβολική γραφή και όχι άλλους τρόπους αναπαράστασης.) Έτσι καταλαβαίνει η νηπιαγωγός αν τελικώς τα παιδιά κατάφεραν να αναπτύξουν την δεξιότητα μέτρησης από ένα αριθμό και μετά, ξεκινώντας από διαφορετικούς αριθμούς -πλην του ενός- την μέτρηση. Με το να συγκρατούν στο νου τους τα παιδιά την ποσότητα των αντικειμένων, χωρίς να χρειάζεται να τα βλέπουν, κατακτούν τα πρώτα στάδια της νοερής αρίθμησης.
Οι δραστηριότητες του σεναρίου αναπτύχθηκαν βασιζόμενες στα ευρήματα των Fusonκαι Herscovics(1986), οι οποίοι υποστηρίζουν πως τα παιδιά στα 5-6 χρόνια γνωρίζουν καλύτερα να μετρούν αλλά χρειάζονται την κατάλληλη εξάσκηση για να πραγματοποιήσουν μετρήσεις, σε αντίθεση με τις απόψεις του Piaget, ο οποίος αναφέρει ότι για να κάνει το παιδί την απαρίθμηση , πρέπει προηγουμένως να έχει αναπτύξει τις προαριθμητικές διαδικασίες και ιδιαίτερα την διατήρηση της ποσότητας, την οποία δεν έχει αναπτύξει πριν τα 6 ή 7 του χρόνια.
Η επιλογή των στόχων που διατυπώθηκαν έγινε με κριτήριο τα βήματα από τα οποία θα πρέπει να περάσει ένα παιδί για να καταφέρει την αρίθμηση από έναν αριθμό και μετά. Πιο συγκεκριμένα, θεωρούμε προαπαιτούμενη την απαρίθμηση και γι’ αυτό το λόγο η πρώτη δραστηριότητα ελέγχει κατά πόσο τα παιδιά πετυχαίνουν αυτήν αλλά και αν έχει γίνει η σύνδεση του αριθμού με την πληθικότητα. Όπως έχουμε επαναλάβει πολλές φορές και πιο πάνω η αρίθμηση είναι το κλειδί για την επίτευξη αυτής. Η επιλογή επομένως της 1ης δραστηριότητας δεν είναι τυχαία. Στη συνέχεια, η 2η δραστηριότητα επιλέχθηκε, γιατί σύμφωνα με τον Van de Walle εισάγει τα παιδιά στην αρίθμηση από έναν αριθμό και μετά, καθώς κρύβοντας ένα μέρος της ορατής συλλογής, το παιδί καλείται να συγκρατήσει στο νου του την ποσότητα που δεν βλέπει, και να συνεχίσει να απαριθμεί. Ωστόσο, ο ίδιος έχει πολλές φορές επισημάνει ότι τα παιδιά στην αρχή μπορεί να δυσκολευτούν να το πετύχουν, όμως με τις επαναλήψεις θα το καταφέρουν τελικώς. Επιπλέον, η τρίτη δραστηριότητα προστέθηκε στο σχέδιο διδασκαλίας, επειδή και πάλι σύμφωνα με τον Van de Walle, βοηθάει τα παιδιά στην καλύτερη κατανόηση αυτής της έννοιας, τα δυσκολεύει αφού προβλέπει τις δοκιμές, επαναλήψεις και τους ελέγχους των ποσοτήτων που καταμετρούν, ενώ απαιτεί τη συνεργασία τους για την συμπλήρωση του φύλλου εργασίας. Τέλος, η 4η δραστηριότητα αποσκοπεί στο πέρασμα των παιδιών από τις διάφορες αναπαραστάσεις των ποσοτήτων των αριθμών και συγκεκριμένα από τις κουκίδες, (οι κουκίδες αναπαριστούν την ποσότητα του αριθμού) στη συμβολική γραφή-μορφή τους, πραγματοποιώντας την τελική σύνδεση αριθμού με πληθικότητα. Τα υλικά που έχουν επιλεγεί θεωρούνται κατάλληλα γιατί βρίσκονται στην καθημερινότητα των παιδιών και μπορούν εύκολα να μετατραπούν σε αναπαραστάσεις ποσοτήτων.
Καφούση, Σ., & Σκουμπουρδή, Χ. (2008). Τα μαθηματικά των παιδιών 4-6 ετών: Αριθμοί και χώρος. Αθήνα: Εκδ. Πατάκης.
Τζεκάκη, Μ. (2007) Μικρά παιδιά, μεγάλα μαθηματικά νοήματα : Προσχολική και πρώτη σχολική ηλικία. Παιδαγωγική Σειρά. Αθήνα : Gutenberg - Γιώργος & Κώστας Δαρδανός
Nunes, T., Bryant, P. (2007) Τα παιδιά κάνουν μαθηματικά. επιμέλεια Δ. Δεσλή (Επιμέλ.). Σ. Λειβαδοπούλου, Γεωργία Σαρηγιαννίδου (Μεταφρ.). Σ. Βοσνιάδου (Επιμελ. Σειράς). Αθήνα : Gutenberg - Γιώργος & Κώστας Δαρδανός
Van de Walle, J. A. (2007). Μαθηματικά για το Δημοτικό και το Γυμνάσιο: Μια εξελικτική διδασκαλία. Θεσσαλονίκη: Εκδ. Επίκεντρο
Πρακτικά 2oυ Πανελλήνιου Εκπαιδευτικού Συνεδρίου Ημαθίας, ανασύρθηκε από: http://www.ekped.gr/praktika10/nip/040.pdf


