Εξοικείωση με τις χωρικές έννοιες και την έννοια της διαδρομής
Submitted by glsakoul on Sat, 06/01/2013 - 17:46Μέσα από τη διδασκαλία, θα αναπαραχθούν μερικές από τις χωρικές έννοιες όπως το «αριστερά, δεξιά, στρίβω δεξιά, στρίβω αριστερά, μπροστά, πίσω, πάνω, κάτω» καθώς και η διόρθωση των κινήσεων όταν χρειάζεται, ο ορισμός της θέσης στο χώρο, η εκμάθηση της έννοιας της διαδρομής και τέλος ο προσανατολισμός στο χώρο. Έτσι λοιπόν, μέσα από τη διεξαγωγή αυτής της δραστηριότητας, τα παιδιά θα επωφεληθούν, αφού θα μπορούν να καθορίσουν με ευκολία εάν ένα αντικείμενο βρίσκεται π.χ. αριστερά τους ή δεξιά τους, αλλά και θα είναι σε θέση να ακολουθήσουν μία διαδρομή με βάση συγκεκριμένες κατευθυντήριες οδηγίες.

Η μαθηματική έννοια με την οποία θα ασχοληθούμε είναι αυτή του χώρου και της διαδρομής. Όσον αφορά το πρώτο σκέλος, ως χώρος ορίζεται το περιβάλλον που είναι άρρηκτα συνδεδεμένο στην ιδέα της απόστασης σε τρεις διαστάσεις. Συγκεκριμένα, ο χώρος, όπως τον αντιλαμβανόμαστε και στον οποίο κινούμαστε,έχει τρεις διαστάσεις. Κάθε στερεό σώμα έχει συγκεκριμένο μήκος, πλάτος και ύψος και μπορεί να κινηθεί και προς τις έξι κατευθύνσεις, δηλαδή εμπρός, πίσω, δεξιά, αριστερά, πάνω ή κάτω, προκειμένου να φθάσει σε κάποιο άλλο σημείο του χώρου. Επίσης, όπως αναφέρεται στο βιβλίο της Τζεκάκη (1998), «ο άνθρωπος χρειάζεται, για να λειτουργήσει μέσα σ’ αυτόν, να διακρίνει τις σχέσεις που συναντά και να τις αναπαραστήσει» (σελ. 35).
Σχετικά με το δεύτερο σκέλος, η διαδρομή δεν αποτελεί την απομνημόνευση μιας προσχεδιασμένης πορείας, αλλά την ικανότητα να ανακαλεί κάποιος τα βήματα με τα οποία φτάνει από ένα σημείο σε ένα άλλο με βάση κάποια στοιχεία ή σημεία αναφοράς που βρίσκονται στον περιβάλλοντα χώρο, τα οποία επηρεάζουν τη σειρά των παραπάνω βημάτων (Τζεκάκη, 1998).
Με τη διδασκαλία που θα διεξάγουμε, θα προωθήσουμε στα παιδιά τη μαθηματική έννοια του χώρου και χωρικές έννοιες όπως οι διαδρομές και οι κατευθύνσεις. Συγκεκριμένα, στο τέλος της διδασκαλίας τα παιδιά θα είναι σε θέση να κατανοήσουν γενικές χωρικές έννοιες όπως αριστερά, δεξιά, πάνω, κάτω αλλά και να ακολουθήσουν μία συγκεκριμένη διαδρομή ανάλογα με τις οδηγίες του/της νηπιαγωγού για την επίτευξη κάποιου στόχου. Επίσης, ένας από τους στόχους της προσπάθειας αυτής, είναι τα παιδιά να αποκτήσουν την ηθική ικανοποίηση ότι αφομοίωσαν κάποιες βασικές έννοιες, εξοικειώθηκαν με αυτές και μπορούν πλέον να προσδιορίσουν το χώρο γύρω τους.
Μερικοί από τους στόχους που επιτυγχάνονται μέσα από τη διδασκαλία μας είναι:
-Τα παιδιά να κατανοήσουν τη θέση τους μέσα στο χώρο και να μπορούν να την προσδιορίσουν σε σχέση με το περιβάλλον και τα αντικείμενά του (γνωστικός)
-Τα παιδιά να μην βλέπουν τα πράγματα γύρω τους μόνο από τη δική τους οπτική γωνία (γνωστικός)
-Να περιγράφουν θέσεις και διαδρομές στο χώρο με τη χρήση απλών χωρικών εννοιών (γνωστικός)
-Να αναπαριστούν θέσεις, διευθύνσεις και διαδρομές σε τετραγωνισμένα περιβάλλοντα (γνωστικός)
-Να αλληλεπιδράσουν με τους συμμαθητές τους μέσα από τη συζήτηση και την ανταλλαγή απόψεων, ενισχύοντας έτσι την ομαδικότητα και τη συνεργασία (συναισθηματικός)
-Να αποκτήσουν μία επιδεξιότητα τόσο με τη χρήση παιδαγωγικού υλικού όπως λαβύρινθου, παζλ, όσο και με αντικείμενα που εμπεριέχονται σε αυτά π.χ. ζάρια, καρτέλες κ.τ.λ. (ψυχοκινητικός)
-Να αναπτύξουν την ικανότητά τους να κινούνται με ευκολία μέσα σε οριοθετημένους χώρους (ψυχοκινητικός)
Σημασία-Σύνδεση με άλλες μαθηματικές έννοιες
Η σημασία αρχικά της έννοιας του χώρου είναι ιδιαίτερα σημαντική, αφού η κατανόησή της επηρεάζει την ενασχόληση των μικρών παιδιών με τα μαθηματικά. Και αυτό γιατί πολλές έρευνες απέδειξαν ότι η επίδοση των μικρών μαθητών με τα μαθηματικά ήταν πολύ καλύτερη από αυτή των μαθητών που δεν είχαν εξοικειωθεί αρκετά με την μαθηματική έννοια του χώρου. Ακόμη, ο χώρος τις πιο πολλές φορές θεωρείται κάτι το αντικειμενικό που «προηγείται της ανθρώπινης εμπειρίας» και είναι χρήσιμο να γνωρίζουμε (Καφούση, 2012). Για να επιτευχθεί αυτό λοιπόν, πρέπει να οξυνθούν οι χωρικές ικανότητες των παιδιών, πράγμα το οποίο αποτελεί και τον λόγο δημιουργίας αυτής της διδασκαλίας.
Επιπλέον, μέσα από την εκμάθηση της μαθηματικής έννοιας είναι δυνατό τα παιδιά να μπορούν να εκφράζονται με άνεση όταν θέλουν να χρησιμοποιήσουν τις χωρικές έννοιες για να δώσουν σαφείς πληροφορίες για τη θέση κάποιου αντικειμένου. Για παράδειγμα, είναι πιθανό κάποιο νήπιο να ζητήσει από το συμμαθητή του να του πει που είναι το παιχνίδι του. Στη συγκεκριμένη περίπτωση απαιτείται το άλλο νήπιο να έχει εξοικειωθεί με τις χωρικές έννοιες ώστε να δώσει μία κατατοπιστική απάντηση.
Ένας ακόμη λόγος για τον οποίο διδάσκουμε αυτή την έννοια είναι επειδή τα νήπια μέσα από την κίνησή τους θα αποκτήσουν τη δυνατότητα να παρατηρούν τον κόσμο γύρω τους και να προσανατολίζονται με βάση κάποιο ορόσημο ή σημείο αναφοράς.
Εκτός όμως από την καθημερινότητά μας, η μαθηματική έννοια του χώρου συνδέεται άρρηκτα και με άλλες μαθηματικές έννοιες όπως η Γεωμετρία. Στο βιβλίο του, «Οι μαθηματικές έννοιες στην Προσχολική Εκπαίδευση και η διδασκαλία τους», ο Ζαχάρος επισημαίνει ότι «η Γεωμετρία ως επιστήμη είναι συνδεδεμένη με τη μελέτη του χώρου». Αυτό είναι πλήρως κατανοητό, αφού τα σχήματα και τα γεωμετρικά σχήματα ορίζονται στον Ευκλείδειο χώρο. Επίσης, αυτές οι δύο μαθηματικές έννοιες συνδέονται επειδή η Γεωμετρία αποτελεί το επόμενο στάδιο για τη διερεύνηση του χώρου. Πιο συγκεκριμένα, τα παιδιά αρχικά για να αναγνωρίσουν τα αντικείμενα που βρίσκονται στο χώρο, εστιάζουν στα εξωτερικά τους χαρακτηριστικά, ενώ στη συνέχεια εστιάζουν στα ευκλείδεια (Piaget). Τέλος, μαζί με τη Γεωμετρία μπορεί να συσχετιστεί και η εκτίμηση της απόστασης καθώς τα παιδιά ήδη από νεαρή ηλικία προσπαθούν να εξερευνήσουν το χώρο, μαθαίνοντας τις σχέσεις μεταξύ των αντικειμένων που βρίσκονται σε αυτόν και τις θέσεις τους σε σχέση με άλλα άτομα που βρίσκονται κοντά τους (είναι δύσκολο σε αυτό το στάδιο να κάνουν το ίδιο και για άτομα που βρίσκονται μακριά τους).
Δεν πρέπει να παραλείψουμε ότι η έννοια του χώρου αποτελεί μία από τις θεματικές ενότητες των Μαθηματικών στο αναλυτικό πρόγραμμα σπουδών. Αυτό γιατί το ΑΠΣ υποστηρίζει ότι τα παιδιά πρέπει να εντοπίζουν και να περιγράφουν θέσεις, διευθύνσεις και διαδρομές στο χώρο ως προς διαφορετικά συστήματα αναφοράς με τη χρήση απλών χωρικών εννοιών, καθώς επίσης και για την ανάγνωση απλών χαρτών και την περιγραφή διαδρομών σε τετραγωνισμένα περιβάλλοντα.
Με βάση τις προηγούμενες πληροφορίες, τα παιδιά προσπαθούν να αναπτύξουν την έννοια του χώρου από πολύ μικρή ηλικία και αυτό διακρίνεται σε τρία στάδια. Κατά το πρώτο στάδιο, το βρέφος ανακαλύπτει τη σχέση του σώματός του με το χώρο στον οποίο αναπτύσσεται. Έπειτα, στο δεύτερο στάδιο το παιδί αρχίζει να πειραματίζεται με τα αντικείμενα και τα περιεργάζεται. Σύμφωνα με τον Piaget, σε αυτό το στάδιο τα παιδιά αρχικά εστιάζουν στα μορφικά χαρακτηριστικά (τοπολογικές και προβολικές σχέσεις). Στη συνέχεια, και μόνο αν ανέπτυξαν τα παραπάνω χαρακτηριστικά, διακρίνουν και τις μετρικές και ευκλείδειες σχέσεις (αποστάσεις, μεγέθη, αναλογίες κ.α.). Στο τρίτο και τελευταίο στάδιο, ο Piaget υποστηρίζει ότι το παιδί εγκαταλείπει την υποκειμενική άποψη που έχει για τον κόσμο (εγωκεντρισμός) και προσεγγίζει αντικειμενικά τον χώρο λαμβάνοντας υπόψιν και τις οπτικές των άλλων.
Την ολοκλήρωση των προηγούμενων σταδίων ακολουθεί η κατανόηση της έννοιας της διαδρομής. Αρχικά, τα παιδιά δεν είναι σε θέση να κατανοήσουν γιατί ακολουθούν τη συγκεκριμένη διαδρομή, αλλά μιμούνται μία κίνηση για να την ακολουθήσουν. Στο επόμενο στάδιο αποκτούν μία νοερή αναπαράσταση της συγκεκριμένης κίνησης (μνήμη της κίνησης) και μπορούν να εξηγήσουν τα βήματά τους.
Δυσκολίες
Πολλές έρευνες έχουν δείξει ότι με τη συγκεκριμένη έννοια τα παιδιά αντιμετωπίζουν κάποιες δυσκολίες. Για παράδειγμα, είναι αποδεδειγμένο ότι έννοιες όπως «πάνω από – κάτω από» δεν μπερδεύουν τόσο τα παιδιά ηλικίας 6 έως 7 ετών, όσο οι έννοιες «μπροστά-πίσω-δεξιά-αριστερά» (Konya, 2006).
Στο βιβλίο της Καφούση αναγράφονται οι παρακάτω δυσκολίες. Κατ’ αρχήν, τα 4-χρονα όταν εξερευνούν το χώρο, μαθαίνουν τις σχέσεις και τις θέσεις των αντικειμένων με βάση ένα σημείο αναφοράς που είναι κοντά τους. Αυτό όμως δεν μπορούν να το πραγματώσουν όταν το σημείο αναφοράς βρίσκεται μακριά τους. Επιπρόσθετα, αν για παράδειγμα δώσουμε στα νήπια δύο διαδρομές ίδιου μήκους, η μία σε ευθεία γραμμή και η άλλη με καμπυλόγραμμη μορφή, θα θεωρήσουν την ευθύγραμμη διαδρομή (που είναι πιο άμεση) ως την πιο μικρή. Είναι σημαντικό να αναφέρουμε ότι τα νήπια μπορούν να κατανοήσουν καλύτερα έναν χώρο όταν τα αντικείμενα που βρίσκονται σε αυτόν είναι σε συμμετρικές θέσεις αντί σε αντισυμμετρικές. Δηλαδή, αν για παράδειγμα τους ζητηθεί να τοποθετήσουν τα αντικείμενα ενός χώρου στη σωστή θέση, αν αυτά βρίσκονται σε άτακτη διάταξη μεταξύ τους, τα νήπια θα ανταποκριθούν δύσκολα στο πλαίσιο της άσκησης. Τέλος, οι δυσκολίες που αντιμετωπίζουν τα παιδιά στην έννοια της διαδρομής και στον εγωκεντρισμό έχουν αναφερθεί παραπάνω.
Οι Clements και Battista υποστηρίζουν ότι τα παιδιά κατανοούν καλύτερα τον χώρο και έχουν καλύτερες επιδόσεις στα μαθηματικά όταν χρησιμοποιούν υλικά. Όπως είναι ευρέως γνωστό, το εκπαιδευτικό υλικό αποτελεί το κύριο μέσο με το οποίο το πρόγραμμα μεταφράζεται σε εκπαιδευτική πράξη. Η Τζεκάκη έχει επισημάνει ότι η έννοια της διαδρομής είναι το μετέπειτα στάδιο της εκμάθησης των βασικών χωρικών εννοιών. Γι’ αυτό το λόγο, καθώς επίσης και γιατί ο Konya έχει αναφέρει πως τα παιδιά παρουσιάζουν δυσκολίες με τις έννοιες μπροστά-πίσω-δεξιά-αριστερά, ένα υλικό που θα μπορούσε να χρησιμοποιηθεί έχει την παρακάτω μορφή:

Συγγραφική ομάδα της εταιρείας SIEM. (2006). Μαθαίνω τα μαθηματικά παρέα με τον Ξεφτέρη 1ο Μέρος: Για παιδιά της Α’ Δημοτικού
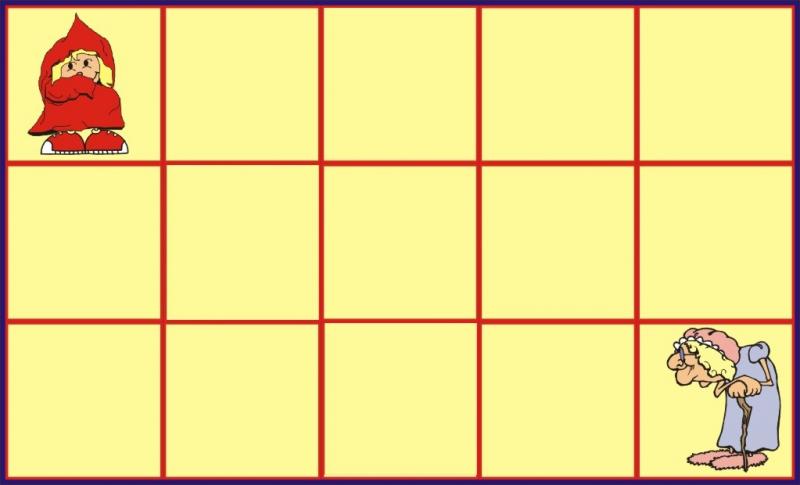
Όπως προαναφέραμε στο πρώτο μέρος, ένας από τους στόχους του ΑΠΣ είναι τα παιδιά να εντοπίζουν, να περιγράφουν και να αναπαριστούν θέσεις, διευθύνσεις και διαδρομές σε τετραγωνισμένα περιβάλλοντα (ΑΠΣ σελ.174). Αυτό μπορούμε να το πετύχουμε με τη χρήση του κάναβου που είναι ένα επίπεδο χωρισμένο σε τέλεια τετράγωνα. Συγκεκριμένα, χρησιμοποιώντας την παρακάτω εικόνα, παρατηρούμε ότι ο χώρος είναι τετραγωνισμένος και υπάρχει αρχή (κοκκινοσκουφίτσα) και τέλος (γιαγιά). Κατά την άποψή μου, τα παιδιά μπορούν να επωφεληθούν μέσα από αυτό το υλικό, γιατί θα κάνουν τα πρώτα τους βήματα στο να ακολουθήσουν μία οποιαδήποτε διαδρομή για να φτάσουν από το ένα σημείο στο άλλο, καθώς και να εξηγήσουν τα βήματά τους.
https://www.npted.org/schools/elrs/Examples/Forms/DispForm.aspx?ID=33
Ακόμη, ως εκπαιδευτικό υλικό μπορούμε να χρησιμοποιήσουμε το παιχνίδι «Φιδάκι», αλλάζοντάς το όμως, έτσι ώστε ο τερματικός σταθμός να έχει ένα δώρο και αντί για φιδάκια να έχουμε κολοκύθες πάνω σε τσουλήθρες (Καφούση, 2012). Συγκεκριμένα, το παιχνίδι παίζεται ακριβώς όπως το «Φιδάκι», με ζάρι, και όταν ο παίχτης πέσει πάνω σε μία κολοκύθα, κατεβαίνει την τσουλήθρα, ενώ αν σταματήσει πάνω σε Άι-Βασίλη ανεβαίνει τη σκάλα. Όποια ομάδα καταφέρει να φτάσει πρώτη στο δώρο, είναι η νικήτρια. Για να προάγουμε την επικοινωνία με μαθηματικούς όρους, μπορούμε να παροτρύνουμε την ομάδα να συζητάει για την επόμενη κίνηση που θα κάνει το πιόνι της (π.χ. θα προχωρήσουμε 4 θέσεις μπροστά και θα ανέβουμε τη σκάλα). Το συγκεκριμένο παιχνίδι μπορεί να θεωρηθεί ίδιο με το κλασσικό φιδάκι που συναντάμε στο διαδίκτυο. Όμως, κατά τη γνώμη μου, η προσθήκη βελακίων καθοδηγεί το παιδί και έτσι εξοικειώνεται με τις έννοιες «στρίβω αριστερά-στρίβω δεξιά», ενώ στο κλασσικό παιχνίδι το παιδί κινεί μηχανικά το πιόνι, χωρίς να του παρέχεται κάποια μορφή υπόδειξης με την οποία θα αντιστοιχίσει χωρικά την κίνησή του. Τα βελάκια λοιπόν, παίζουν σημαντικό ρόλο γιατί σύμφωνα με τον Konya τα παιδιά δυσκολεύονται περισσότερο με τις έννοιες «μπροστά-πίσω-δεξιά-αριστερά».

Ένα άλλο είδος παιδαγωγικού υλικού είναι η διαδρομή μέσα σε όρια (Sheffield, 1998). Πιο αναλυτικά, ένα παιδί πρέπει να διασχίσει ένα μονοπάτι για να φτάσει στον φίλο του που είναι στο τέλος του μονοπατιού, χωρίς όμως να παραβεί τα όρια του χώρου που έχει ορίσει ο/η νηπιαγωγός. Όμως, ο φίλος του μπορεί να μην βρίσκεται μέσα στο μονοπάτι, άρα να μην μπορεί να τον φτάσει. Έτσι, τα παιδιά θα μάθουν ότι η κίνηση μέσα σε συγκεκριμένα όρια αποτελεί μία διαδρομή και τις έννοιες «μέσα από – έξω από». Η σημασία του υλικού αυτού φαίνεται στο γεγονός ότι η Τζεκάκη αναφέρει πως τα παιδιά θα μάθουν να ακολουθούν μία διαδρομή εμπειρικά και όχι από την απομνημόνευσή της και να μάθουν να οργανώνουν καλύτερα το χώρο τους.
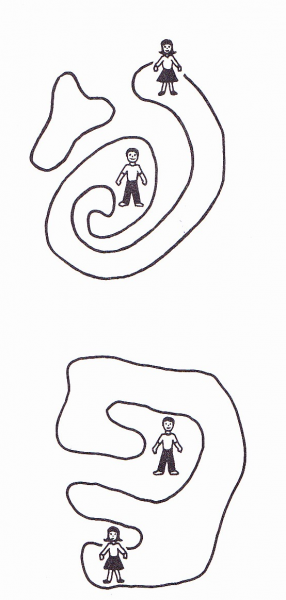

(α) (β)
(α) Cruikshank & Sheffield. (1998). Teaching Mathematics to Elementary School Children, A Foundation For The Future
(β) Dienes, P. Z. & Holt, M. (1972). ZOO
Επίσης, ο λαβύρινθος μπορεί να μας βοηθήσει στο σχεδιασμό της διδασκαλίας (Sheffield, 1998). Μία τέτοια επιλογή κατά τη γνώμη μου, θα προσέδιδε μία ωραία πινελιά αφού σύμφωνα με τον συγγραφέα οι λαβύρινθοι προσελκύουν το ενδιαφέρον των παιδιών γιατί δημιουργείται το αίσθημα στο παιδί ότι πρέπει να το λύσει. Ακόμη, αποτελούν ένα παζλ του οποίου η δυσκολία αυξομειώνεται ανάλογα με την ηλικία του παιδιού και τα ίδια τα παιδιά εξοικειώνονται με την έννοια της διαδρομής και γίνονται λύτες του προβλήματος. Πρέπει να επισημανθεί ότι η προσθήκη του λαβύρινθου στην προσπάθειά μας να μεταδώσουμε τις έννοιες χώρος-διαδρομές θα είναι ιδιαίτερα χρήσιμη, αφού και οι δύο έννοιες εμπεριέχονται σε αυτόν. Επίσης, το συγκεκριμένο παιδαγωγικό υλικό είναι αρκετά ευέλικτο ως προς τη χρήση του. Και αυτό γιατί μπορούμε να επιλέξουμε είτε τα παιδιά να σχεδιάσουν έναν λαβύρινθο και να δημιουργήσουν μία σωστή διαδρομή ώστε να υπάρχει έξοδος από αυτόν, είτε τα ίδια να συμμετέχουν σε παιχνίδια με λαβύρινθους όπου θα πρέπει να τους διασχίσουν (φύλλο εργασίας).
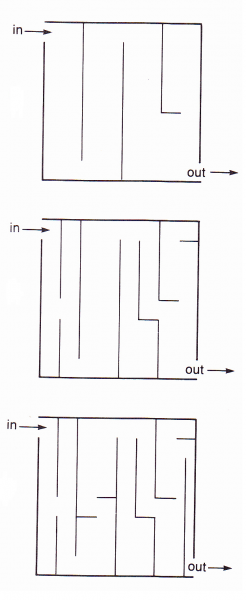

(α) (β)
(α) Cruikshank & Sheffield. (1998). Teaching Mathematics to Elementary School Children, A Foundation For The Future
(β) Σιάκη, Μ. & Φούρκα, Π. (2006). Παιχνίδια για όλες τις εποχές για παιδιά 4-6 ετών.
Επιπλέον, πρέπει να αναφέρουμε ένα από τα δημοφιλέστερα παιδαγωγικά υλικά που προάχθηκαν μέσα από την LOGO (Seymour Papert), το Bee-Bot. Ο ίδιος ο Seymour Papert υποστήριξε ότι η παιδαγώγηση μέσω της LOGO κατασκευάζει και ανακατασκευάζει τη γνώση με τον δικό μας μοναδικό τρόπο. Πιο αναλυτικά, το Bee-Bot αποτελεί ένα προγραμματιζόμενο ρομποτάκι-μελισσούλα, το οποίο έχει πάνω του κουμπάκια με τα οποία κινείται πάνω-κάτω-δεξιά-αριστερά. Θα μπορούσαμε να χρησιμοποιήσουμε το Bee-Bot σε συνδυασμό με ένα επιτραπέζιο στο οποίο τα παιδιά θα πρέπει να κατευθύνουν το ρομποτάκι ανάλογα με την ιστορία που έχει πει προηγουμένως ο/η νηπιαγωγός. Έτσι, τα νήπια θα μάθουν να συλλογίζονται με μαθηματικό τρόπο, αφού θα πρέπει να προγραμματίσουν τα ίδια τις κινήσεις της μελισσούλας, έτσι ώστε να φτάσει με επιτυχία στο προορισμό της και να αποφύγει τα εμπόδια (χειραπτικό υλικό με επεκτάσεις ψηφιακού).



Ερευνώντας την ενδεικτική βιβλιογραφία και τις θεωρητικές συζητήσεις που αποτυπώνονται σ’ αυτή, το πλαίσιο στο οποίο θα κινηθεί η διδασκαλία μας χαρακτηρίζεται από τις εξής βασικές αρχές:
-
Ο ρόλος της/του νηπιαγωγού θα είναι καθοδηγητικός, όταν χρειάζεται, με τη χρήση ερωτήσεων και δεν θα παρέχει τη λύση αυτούσια
-
Θα δίνεται η δυνατότητα στα παιδιά να πειραματιστούν με τα διάφορα παιδαγωγικά υλικά, αλλά και να διορθώσουν τυχόν λάθος επιλογές τους όταν συναντάνε αδιέξοδο
-
Τα παιδιά θα μπορούν να συνεργαστούν μεταξύ τους και να συζητούν για πιθανές λύσεις στα προβλήματα
«Βοηθώντας την Κοκκινοσκουφίτσα να βρει το δρόμο της»
Μέγεθος Τάξης: 15 με 20 παιδιά (14-16 νήπια & 4 προνήπια)
Ηλικία Παιδιών: 4 έως 6 χρονών
Εκτιμώμενη Διάρκεια: το σενάριο θα διαρκέσει μία διδακτική ημέρα
Υλικά: βιβλίο (παραμύθι), χάρτης-ζωγραφιά, χαρτί του μέτρου, λαβύρινθος, κάναβος, bee-bot, καρτέλες, μαρκαδόροι, σχοινάκια, στεφάνια και φύλλα εργασίας
Μέθοδοι: ομαδοσυνεργατική, καθοδηγητική, διερευνητική, παρατήρηση,περιγραφή
Τεχνικές, μέσα: παιχνίδι (δομημένο), αφήγηση παραμυθιού, ερωτοαπαντήσεις
Προαπαιτούμενη γνώση: Για την ομαλή διεξαγωγή της διδασκαλίας, τα παιδιά αναμένεται να γνωρίζουν σε βασικό επίπεδο χωρικές έννοιες όπως «αριστερά, δεξιά, πάνω και κάτω» και την αρίθμηση μέχρι το 10.
Συμβατότητα με ΑΠΣ: Το συγκεκριμένο κεφάλαιο εντάσσεται στην ενότητα του ΑΠΣ «Χώρος και Γεωμετρία – Μέτρηση» και κατατάσσεται στο γενικότερο στόχο «Οι μαθητές να εντοπίζουν και να περιγράφουν θέσεις, διευθύνσεις και διαδρομές στο χώρο ως προς τα διαφορετικά συστήματα αναφοράς με τη χρήση απλών χωρικών εννοιών»
Γενικός σκοπός: Μέσα από το συγκεκριμένο σενάριο τα παιδιά θα εξοικειωθούν με την έννοια της διαδρομής και την κίνηση σε οριοθετημένο χώρο.
Επιμέρους στόχοι:
α)Να κινούνται σε οριοθετημένες διαδρομές όπου το μονοπάτι είναι μοναδικό,
β)Να μπορέσουν να επιλύσουν τόσο με τις χωρικές έννοιες όσο και με τον προγραμματισμό κινήσεων το πρόβλημα του λαβύρινθου για να σωθεί η κοκκινοσκουφίτσα,
γ)Να μπορέσουν να αντιληφθούν τα λάθη τους, να τα προσδιορίσουν και να τα διορθώσουν,
δ)Να αναγνωρίσουν τη σωστή διαδρομή που θα ακολουθήσουν και να τη σχεδιάσουν χωρίς να ζωγραφίσουν πάνω από τα εμπόδια ή να βγουν από τα όρια του λαβύρινθου,
ε)Να επικοινωνούν με μαθηματικούς όρους (χωρικές έννοιες),
στ)Να αναγνωρίζουν τη σημασία της μαθηματικής έννοιας χρησιμοποιώντας τις εμπειρίες τους στη καθημερινή ζωή,
η)Να αναπτύξουν το ομαδικό τους πνεύμα μέσα από τη συζήτηση και την ανταλλαγή απόψεων.
Δραστηριότητα 1η (Εισαγωγή των παιδιών στην έννοια «χώρος-μονοπάτι» μέσω του παραμυθιού)
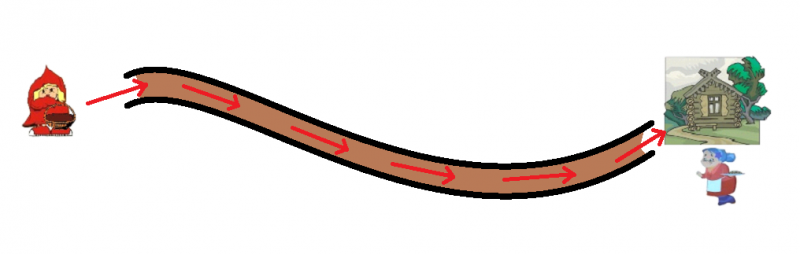
Ο/Η νηπιαγωγός αφήνει σε εμφανές σημείο στη γωνιά της παρεούλας το παραμύθι της κοκκινοσκουφίτσας και ρωτάει τα παιδιά: «Μπορεί κάποιο παιδάκι να μου φέρει το παραμυθάκι που έχω αφήσει στο τραπέζι;». Αφού της το δώσει κάποιο από τα παιδιά, τους λέει: «Έχετε ακούσει το παραμύθι με την κοκκινοσκουφίτσα; Θέλετε να το θυμηθούμε;». Έτσι λοιπόν ξεκινάει η αφήγηση του παραμυθιού, απλοποιημένο όμως ώστε να ικανοποιεί τις ανάγκες μας. Συγκεκριμένα, ο/η νηπιαγωγός αφηγείται στα μικρά παιδιά ότι η κοκκινοσκουφίτσα είχε χαθεί στο δάσος και φοβόταν τον κακό λύκο. Το μόνο που της έμενε ήταν να βρει το σωστό μονοπάτι και να φτάσει γρήγορα στη γιαγιά της σώα και αβλαβής. Εκείνη τη στιγμή, ο/η νηπιαγωγός βγάζει από την τσάντα της ένα φύλλο Α4 που πάνω του έχει ζωγραφίσει ένα μονοπάτι και ρωτάει: «Μπορεί κάποιο παιδάκι να πει στην κοκκινοσκουφίτσα που να πάει για να φτάσει στη γιαγιά της;». Με αυτόν τον τρόπο και από τις απαντήσεις των παιδιών, ο/η νηπιαγωγός θα αντιληφθεί ποιο είναι το γνωστικό υπόβαθρο των παιδιών για τη συγκεκριμένη μαθηματική έννοια. Αν παρατηρήσει ότι τα παιδιά δυσκολεύονται, κάνει ο ίδιος/η ίδια την αρχή και δίνει οδηγίες. Επίσης, επέλεξα να ξεκινήσω έτσι τη δραστηριότητά μου, επειδή η Χρονάκη αναφέρει ως κύριο χαρακτηριστικό της χωρικής σκέψης το σημειωτικό σύστημα, το οποίο εκφράζεται μέσα από γραφικές και οπτικές αναπαραστάσεις όπως ο χάρτης-ζωγραφιά και οι οδηγίες πάνω στη ζωγραφιά με σχήματα και βέλη (Καφούση, 2012).

Δραστηριότητα 2η (Παιχνίδι με λαβύρινθο)
Αφού ολοκληρωθεί το πρώτο βήμα της διδασκαλίας, ο/η νηπιαγωγός έχει προετοιμαστεί απομακρύνοντας τα καρεκλάκια από τη γωνιά της παρεούλας και έχει ζωγραφίσει πάνω σε ένα χαρτί του μέτρου 3 με 4 σχέδια ώστε να μην καθυστερήσει η δραστηριότητα. Χωρίζει λοιπόν τα παιδιά σε ομάδες των 5-6 ατόμων και τα ενθαρρύνει να μπουν τα ίδια στο ρόλο της κοκκινοσκουφίτσας, βάζοντάς τα σε μικρούς και απλούς λαβύρινθους. Πιο συγκεκριμένα, οι λαβύρινθοι θα έχουν μορφές που φαίνονται στην εικόνα. Αρχικά, θα βρίσκεται μέσα σε αυτούς ένα παιδί την φορά, το οποίο προσπαθεί να βρει την έξοδο χωρίς να βγει από τα όρια και τα υπόλοιπα θα συζητάνε μεταξύ τους πάνω σε αυτό που βλέπουν μέχρι να έρθει η σειρά τους. Για παράδειγμα,
Π: «Μήπως πρέπει να κινηθεί πιο δεξιά;»
N: «Σωστά παιδιά!!! »
Π: «Αν συνεχίσει έτσι θα βγει από το λαβύρινθο!»
Ν: «Τι προτείνετε να κάνει;»
Π: «Αντρέα πήγαινε πιο αριστερά!»
Πρέπει να αναφέρουμε ότι από τη στιγμή που η τάξη αποτελείται και από προνήπια, υπάρχει η πιθανότητα τα ίδια να βγουν από τα επιτρεπτά όρια του λαβύρινθου. Σε αυτή την περίπτωση, ο/η νηπιαγωγός θα ήταν συνετό να παροτρύνει τα παιδιά να ξεκινήσουν πάλι από την αρχή του λαβύρινθου την όλη διαδικασία συμβουλεύοντάς τα και όχι να τους πει κατευθείαν το σωστό μονοπάτι. Για παράδειγμα, ο/η εκπαιδευτικός θα μπορούσε να κάνει ερωτήσεις όπως: «Γιωργάκη αν ακολουθήσεις το μονοπάτι που πήρες στην αρχή θα βγεις από τη χρωματιστή γραμμή ή όχι;», «Μπορείς να προσπαθήσεις ξανά χωρίς να πατήσεις τη χρωματιστή γραμμή;». Έτσι, τα παιδιά θα καταλάβουν καλά ότι πρέπει να παραμείνουν μέσα στα όρια του λαβύρινθου και να βρουν την έξοδο.
Αποφασίσαμε να συνεχίσουμε με αυτό τον τρόπο τη δραστηριότητά μας, έτσι ώστε τα νήπια να εξοικειωθούν με μία απλοποιημένη μορφή λαβύρινθου και να αρχίσουν να ξεφεύγουν από το στάδιο της μίμησης της κίνησης.

Δραστηριότητα 3η (Παιχνίδι διαδρομών με bee-bot ως προπαρασκευαστικό στάδιο)
Ύστερα από το παιχνίδι που διαδραματίστηκε, ο/η νηπιαγωγός προετοιμάζει το χώρο τοποθετώντας ένα χαλάκι για να καθίσουν τα νήπια και τους ρωτάει «Θέλετε να παίξουμε ένα παιχνίδι;». Στη συνέχεια, τους δείχνει το ρομποτάκι λέγοντάς τους ότι είναι φίλος της κοκκινοσκουφίτσας και χρειάζεται τη βοήθειά μας, γιατί μπορεί να μην τα καταφέρει μόνο του. Έτσι λοιπόν, αρχίζει να τους κάνει διάφορες ερωτήσεις όπως:
«Ξέρετε τι είναι αυτό που κρατάω;»
«Σας θυμίζει τίποτα;»
«Τι πιστεύετε ότι μπορεί να είναι;»
Σε αυτό το σημείο, αν παρατηρήσει ότι μερικά παιδιά δεν αναγνωρίζουν το bee-bot, τους εξηγεί τί είναι και πώς λειτουργεί μέσα από τις βοηθητικές καρτέλες που απεικονίζονται παραπάνω. Έπειτα, αφού καθίσουν όλοι μαζί στη γωνιά της συζήτησης, ο/η εκπαιδευτικός τους παρουσιάζει ένα χάρτη (παρουσιάζεται παρακάτω η εικόνα) που έχει προετοιμάσει στον υπολογιστή και έχει εκτυπώσει σε μακέτα προηγουμένως και τους εξηγεί ότι σκοπός του παιχνιδιού είναι να «πουν» στο ρομποτάκι να δείξει τη διαδρομή που πρέπει να ακολουθήσει η κοκκινοσκουφίτσα για να φτάσει στη γιαγιά της. Επίσης, τους εξηγεί ότι όσες φορές πατήσουν κάποιο κουμπάκι, τόσες φορές θα κινηθεί το bee-bot προς την αντίστοιχη κατεύθυνση και ότι αφού πατήσουν τη σειρά των κινήσεων πρέπει να πατήσουν το GO. Αντίθετα, αν αλλάξουν γνώμη για την απόφασή τους, μπορούν να πατήσουν το CLEAR και να ξαναδώσουν τις εντολές. Σε αυτό το σημείο, θα προτρέψει τα παιδιά να δοκιμάσουν το bee-bot σε μία απλή διαδρομή, ώστε να κατανοήσουν τη λειτουργία του πριν προχωρήσουν στο επόμενο επίπεδο. Έπειτα, στα πλαίσια της κύριας δραστηριότητας, τους επισημαίνει ότι πρέπει να επιλέξουν μία διαδρομή χωρίς να συναντήσουν τον λύκο μπροστά τους. Κατά τη διάρκεια του παιχνιδιού κάποιες ενδεικτικές ερωτήσεις που μπορεί να διατυπωθούν είναι:
Ν: «Τώρα που φτάσατε στο δάσος, ποιο πιστεύετε ότι θα είναι το επόμενό σας βήμα;»
Π1: «Θα πάμε μπροστά για να είμαστε πιο κοντά στη γιαγιά!»
Π2: «Θα κινηθούμε δεξιά!»
Ν: «Αν πας δεξιά, δεν κινδυνεύεις να σε φάει ο λύκος;»
Αυτή η μικρή δραστηριότητα θα αποτελέσει προπαρασκευαστικό στάδιο για το επόμενο βήμα που θα ακολουθήσει. Αυτό γιατί, τα νήπια θα είναι σε θέση να διορθώνουν τα λάθη τους και να ξαναδοκιμάζουν χρησιμοποιώντας το πολύ ενδιαφέρον παιχνιδάκι bee-bot. Επίσης, θα έχουν την ικανότητα να εξηγούν τα βήματά τους, πράγμα που πιο πριν πιθανόν να μην μπορούσαν.


Δραστηριότητα 4η (Προσπάθεια των νηπίων στην εύρεση της σωστής διαδρομής)
Έπειτα, ο/η εκπαιδευτικός ζητάει από τα παιδιά να μετακινηθούν στη γωνιά των εικαστικών όπου έχει ενώσει τα τραπεζάκια και έχει τοποθετήσει πάνω σε αυτά τους μαρκαδόρους. Αφού τα χωρίσει σε ομάδες των τριών με τεσσάρων ατόμων, μοιράζει σε κάθε ομάδα εκτυπωμένο τον κόσμο της κοκκινοσκουφίτσας σε μορφή λαβύρινθου (τον οποίο έχει ο/η ίδιος/α δημιουργήσει) και τους εξηγεί: «Παιδιά, για να φτάσει η κοκκινοσκουφίτσα στη γιαγιά της δεν πρέπει να περάσει μέσα από τα δένδρα αλλά να ακολουθήσει το μονοπάτι του δάσους». Όπως παρατηρούμε από την παρακάτω εικόνα στη μία μεριά του λαβύρινθου απεικονίζεται η κοκκινοσκουφίτσα που εισέρχεται στο δάσος και στη άλλη πλευρά το σπίτι της γιαγιάς. Συγκεκριμένα, τα παιδιά πρέπει να ζωγραφίσουν πάνω στο φύλλο εργασίας τον δρόμο που πρέπει να ακολουθήσει η κοκκινοσκουφίτσα για να φτάσει στο στόχο της, παραμένοντας όμως μέσα στο δάσος.
Καθ’ όλη τη διάρκεια της δραστηριότητας, ο/η νηπιαγωγός παροτρύνει τα παιδιά να συζητούν μεταξύ τους και να κάνουν προβλέψεις για την πιθανή λύση του προβλήματος. Επίσης, όταν είναι αναγκαίο, ο ρόλος του/της είναι επικουρικός, ενισχύοντας τις προβλέψεις των παιδιών μέσω των καθοδηγητικών ερωτήσεων όπως:
Ν: «Σε αυτό το σημείο που βρίσκεται τώρα η κοκκινοσκουφίτσα, ποια κατεύθυνση νομίζετε πως θα ακολουθήσει;»
Π: «Προς τα επάνω!»
Ν: «Αν πάει προς τα πάνω, θα τη βοηθήσει τελικά να βρει το δρόμο της;»
Ν: «Ποια διαδρομή θα πάρετε για να αποφύγετε τον κακό λύκο;»
Π: «θα στρίψουμε δεξιά!»
Ν: «Σε αυτό το σημείο που βρίσκεται η κοκκινοσκουφίτσα, πιστεύετε ότι πρέπει να κατευθυνθεί προς τα πάνω ή προς τα κάτω;»
Π: «Προς τα κάτω, γιατί νααα τοοο σπιτάκι!!!»
Σε σχέση με τα προηγούμενα στάδια, επιλέξαμε να τοποθετήσουμε περισσότερα εμπόδια και να δημιουργήσουμε έναν πιο περίπλοκο κόσμο, διότι τα νήπια έχουν εξοικειωθεί ήδη στο να ακολουθούν μία διαδρομή με λιγότερα εμπόδια. Έτσι, αφού έχουμε έναν πιο οριοθετημένο χώρο, θα ελέγχουν περισσότερο τις κινήσεις τους. Αποφασίσαμε να συνεχίσουμε με αυτό το υλικό τη διδασκαλία μας, επειδή στο βιβλίο του Sheffield, όπως αναφέραμε, τα παιδιά βρίσκουν πολύ ενδιαφέρον να λύνουν προβλήματα με λαβύρινθους.

Αξιολόγηση
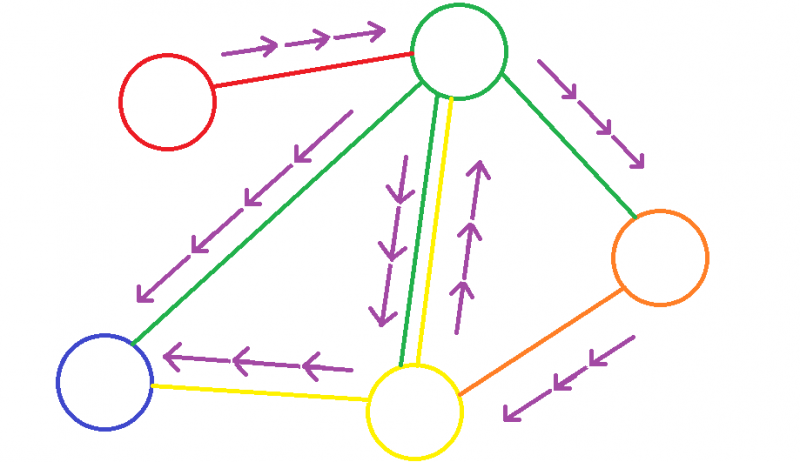
Τέλος, θέλοντας ο/η νηπιαγωγός να αξιολογήσει τα παιδιά ως προς τους στόχους που τέθηκαν παραπάνω, τα μαζεύει στο προαύλιο όπου έχει τοποθετήσει στεφάνια που ενώνονται μεταξύ τους με χρωματιστά σχοινάκια. Τους εξηγεί λοιπόν ότι πρέπει να ακολουθήσουν τη διαδρομή που θα περιγράφει ο χάρτης που θα τους δοθεί (δημιουργία του/της νηπιαγωγού). Λαμβάνοντας υπόψιν ότι η τάξη αποτελείται από 15 με 20 παιδιά, ο/η νηπιαγωγός δημιουργεί 4 με 5 διαφορετικούς χάρτες και τους μοιράζει τυχαία στα παιδιά. Αυτό θα γίνει με βάση τον γενικό χάρτη που φαίνεται παρακάτω, αφαιρώντας σε κάθε ένα συγκεκριμένες διαδρομές (βελάκια) για τη δημιουργία νέων. Έτσι, αν ακολουθήσουν σωστά τη διαδρομή, θα σημαίνει ότι έχουν κατανοήσει την έννοια της διαδρομής στο χώρο.
Ζαχάρος, Κ. (2007). Οι μαθηματικές έννοιες στην προσχολική εκπαίδευση και η διδασκαλία τους. Επιστήμες της Αγωγής · Διδακτική - Αναλυτικά Προγράμματα - Αξιολόγηση. Β. Βασιλού - Παπαγεωργίου (Επιμελ. Σειράς). Αθήνα : Μεταίχμιο
Καφούση, Σ., & Σκουμουρδή, Χ. (2012). Τα μαθηματικά των παιδιών από 4-6 ετών: Αριθμοί και χώρος. Αθήνα: Εκδ.Πατάκης
Παιδαγωγικό Ινστιτούτο. (2011). Πρόγραμμα Σπουδών Νηπιαγωγείου
Σιάκη, Μ. & Φούρκα, Π. (2006). Παιχνίδια για όλες τις εποχές για παιδιά 4-6 ετών. Αθήνα: Εκδ.Πατάκης
Συγγραφική ομάδα της εταιρείας SIEM. (2006). Μαθαίνω τα μαθηματικά παρέα με τον Ξεφτέρη 1ο Μέρος: Για παιδιά της Α’ Δημοτικού. Εκδ.Άγκυρα
Τζεκάκη, Μ. (2011). Μαθηματική Εκπαίδευση για την Προσχολική και Πρώτη Ηλικία. Θεσσαλονίκη: Ζυγός
Χρονάκη, Α (2012). Διδακτικές σημειώσεις για το μάθημα : 'Ανάπτυξη της Μαθηματικής Σκέψης στις μικρές ηλικίες και διδακτική πράξη' για το ακαδημαικό έτος 2012-2013
Cruikshank & Sheffield. (1998). Teaching Mathematics to Elementary School Children, A Foundation For The Future. Οχάιο: Εκδ.Merrill
Dienes, P. Z. & Holt, M. (1972). ZOO. Barcelona: Εκδ.Teide
Neath Port Talbot Learning Getaway (n.d). Education Library and Resource Service/Examples/Miscellaneous. https://www.npted.org/schools/elrs/Examples/Forms/DispForm.aspx?ID=33