Διαίρεση – Μοίρασμα
Submitted by ltme on Fri, 11/29/2013 - 19:48
Η ομαδική αυτή εργασία έχει σαν θέμα: «Η Διαίρεση- μοίρασμα στο Νηπιαγωγείο». Αρχικά αναλύεται η μαθηματική έννοια της διαίρεσης μερισμού, στη συνέχεια σχεδιάζεται η διδασκαλία και η διδακτική παρέμβαση καθώς και τα μέσα που θα χρησιμοποιηθούν για τη διδακτική αυτή παρέμβαση, έπειτα εφαρμόζεται στην πράξη η διδακτική παρέμβαση και τέλος, αναλύονται τα αποτελέσματα και καταγράφονται τα συμπεράσματα. Ειδικότερα, αποφασίσθηκε η έννοια της διαίρεσης μερισμού να παρουσιασθεί στα παιδιά μέσα από την ενότητα της γλώσσας (προφορικός λόγος, λογοτεχνία) με αποτέλεσμα να συνδυαστούν τα μαθηματικά με αυτήν και να γίνουν πιο ελκυστικά για τα παιδιά. Ειδικότερα, χρησιμοποιήθηκε ένα αυτοσχέδιο παραμύθι ως πλαίσιο προκειμένου να εισαχθούν τα παιδιά στην έννοια, στο οποίο αναφέρονται προβλήματα διαίρεσης. Επίσης, η γλώσσα συνδυάστηκε με τα μαθηματικά διαμέσου του διαλόγου. Η διαλογική διδασκαλία συνέβαλε στο να εκφράσουν τα παιδιά τις απόψεις τους για τα προβλήματα της διαίρεσης που προέκυψαν μέσα από το παραμύθι, να κάνουν προβλέψεις για τις πιθανές λύσεις και να επιβεβαιώσουν τις προβλέψεις αυτές μέσα από την πράξη. Σημειωτέον ότι τα υλικά που χρησιμοποιήθηκαν ήταν προσιτά και οικεία στα παιδιά, δηλαδή υλικά από το περιβάλλον της τάξης τους (καφασάκια, φρούτα, μολύβια, πλαστικοποιημένα λαγουδάκια και καρότα) αλλά και σχετικό λογισμικό υλικό. Στη συνέχεια, πραγματοποιήθηκε ανατροφοδότηση της έννοιας διαίρεσης μερισμού και κάθε παιδί υλοποιούσε στην πράξη την έννοια αυτή, τόσο με εποπτικό χειραπτικό υλικό όσο και μέσω του λογισμικού. Επίσης, στο τέλος κάθε δραστηριότητας δόθηκαν στα παιδιά φύλλα εργασίας προκειμένου να πραγματοποιηθεί η αξιολόγηση και κατά πόσο τα παιδιά κατανόησαν τη διαδικασία και την έννοια της διαίρεσης του μερισμού. Τα αποτελέσματα δε της αξιολόγησης κρίνονται ενθαρρυντικά.

Εισαγωγή: Η εργασία αυτή απευθύνεται σε παιδιά προσχολικής ηλικίας. Η διδακτική παρέμβαση και διδασκαλία σχεδιάστηκε και εφαρμόσθηκε με τρόπο που να ανταποκρίνεται στο ηλικιακό και αναπτυξιακό επίπεδο των παιδιών του νηπιαγωγείου. Ως γενικός σκοπός αυτής της εργασίας είναι να εξοικειωθούν τα παιδιά με την έννοια της διαίρεσης μερισμού καθώς επίσης να εξοικειωθούν με τη χρήση της τεχνολογίας.
Οι κύριοι στόχοι της εργασίας είναι: (1)Να ανοιχθεί ένα πρώτο παράθυρο στις νοητικές διαδικασίες των παιδιών αναφορικά με την έννοια της διαίρεσης και στις μελλοντικές επεκτάσεις της έννοιας αυτής στις επόμενες βαθμίδες της εκπαίδευσης. (2)Να έλθουν τα παιδιά σε επαφή με προβλήματα διαίρεσης κατά τα οποία, σε άλλες περιπτώσεις υπάρχει υπόλοιπο, και σε άλλες όχι. (3)Να μοιράζουν μικρές ποσότητες αντικειμένων. (4)Να αποκτήσουν τα παιδιά δεξιότητες αρίθμησης και αντιστοιχίας. (5)Να καλλιεργηθεί το ομαδοσυνεργατικό πνεύμα και η αλληλεπίδραση μεταξύ των παιδιών αναφορικά με την επίλυση προβλημάτων διαίρεσης μερισμού. (6)Να εμπλουτίσουν το λεξιλόγιό τους μέσω του προφορικού λόγου και δη να εξοικειωθούν με τυπικές μαθηματικές έννοιες όπως «διαιρώ» αλλά και άτυπες όπως «μοιράζω». (7)Να αξιοποιήσουν την τεχνολογία (ηλεκτρονικό υπολογιστή και ψηφιακό λογισμικό) για επίλυση προβλημάτων διαίρεσης.
Το θέμα της διαίρεσης μερισμού είναι σημαντικό υπό την προϋπόθεση ότι έχει νόημα για το ίδιο το παιδί. Έχει νόημα για το παιδί καθόσον εμπλέκεται σε διαδικασίες που θα το βοηθήσουν να μοιραστεί αντικείμενα με τους συμμαθητές του και γενικά διαδικασίες που αποτελούν μέρος της καθημερινής του πρακτικής. Η εργασία αυτή κινείται στα πλαίσια του Αναλυτικού Προγράμματος και της διαθεματικής διδασκαλίας. Σύμφωνα με το ΔΕΠΠΣ τα παιδιά επιδιώκεται να μάθουν να «εκτελούν» απλές μαθηματικές πράξεις, να χειρίζονται ποσότητες να μοιράζουν ποσότητες σε διαφορετικές καταστάσεις, να εμπλουτίζουν τη γλώσσα με λέξεις που συνδέονται με τα μαθηματικά, να επικοινωνούν και να αξιοποιούν την τεχνολογία. Η διδακτική αυτή παρέμβαση πραγματοποιήθηκε στο 26ο Νηπιαγωγείο Βόλου, και ειδικότερα στο ολοήμερο τμήμα αυτού. Η χρήση της τεχνολογίας βοήθησε σημαντικά τα παιδιά και ιδιαίτερα στην εξοικείωσή τους με την έννοια της διαίρεσης μερισμού και αποτέλεσε αφορμή να επικοινωνήσουν τα παιδιά με την πράξη της διαίρεσης μέσω ενός παιγνιώδους και ελκυστικού πλαισίου. Μέσω του ψηφιακού λογισμικού Kidspiration τα παιδιά ανέπτυξαν την παρατηρητικότητά τους και είχαν διαφορετικές δυνατότητες σε σχέση με αυτές που θα είχαν αν παρέμεναν απλά και μόνο στη χρήση του παραδοσιακού και χειραπτικού υλικού. Σημαντικό επίσης, ήταν το γεγονός ότι σε περίπτωση λάθους η διόρθωση εκ μέρους των παιδιών ήταν εύκολη. Τα παιδιά έλυσαν προβλήματα διαίρεσης μερισμού σε δύο φάσεις: α) στην πρώτη φάση κάθε παιδί μοίρασε αντικείμενα χωρίς να μένει υπόλοιπο και β) στη δεύτερη φάση μοίρασε αντικείμενα όπου έμενε υπόλοιπο.
Τέλος, η εργασία πραγματοποιήθηκε σε δύο ενότητες: (Α) Στην πρώτη ενότητα ελέγχθηκαν οι δυνατότητες των παιδιών να απαριθμούν τα στοιχεία ενός συνόλου, να κάνουν αντιστοιχίσεις και οι γνώσεις τους σχετικά με τη διαίρεση μερισμού. (Β) Στη δεύτερη ενότητα μέσω δραστηριοτήτων με χειραπτικό υλικό και τη χρήση του λογισμικού Kidspiration κάθε παιδί πραγματοποίησε τη διαίρεση μερισμού με φρούτα που καλούνταν τα παιδιά να τα μοιράσουν σε καλάθια και στη συνέχεια μέσω του ως άνω λογισμικού τα παιδιά κλήθηκαν να μοιράσουν φρούτα σε καλάθια και φρούτα σε γουρουνάκια. Επίσης, δόθηκαν στα παιδιά φύλλα αξιολόγησης προκειμένου να ελεγχθεί η αφομοίωση και εμπέδωση της έννοιας από τα παιδιά. Τα συμπεράσματα στα οποία κατέληξε η ερευνητική ομάδα επιγραμματικά αναφερόμενα είναι ενθαρρυντικά. Τα παιδιά ήταν εξοικειωμένα με την έννοια της διαίρεσης ήδη από το οικογενειακό τους περιβάλλον. Μπορούσαν να απαριθμούν ποσότητες χωρίς καμία δυσκολία. Η επίλυση προβλημάτων διαίρεσης από κάποια παιδιά γίνονταν αυτόματα χωρίς να χρησιμοποιήσουν το υλικό που τους δόθηκε. Για παράδειγμα στο πρόβλημα διαίρεσης έχουμε τρία καλαθάκια και έξι φρουτάκια. Για να μοιραστούν δίκαια τα φρουτάκια από πόσα πρέπει να έχει το κάθε καλάθι, τα παιδιά απάντησαν αυτόματα από δυο χωρίς να το κάνουν στην πράξη. Σε αρκετές περιπτώσεις που τους δόθηκαν προβλήματα διαίρεσης με υπόλοιπο, συνδύασαν την επίλυση του προβλήματος με την πράξη της αφαίρεσης. Όσον αφορά στη χρήση του ηλεκτρονικού υπολογιστή και του ψηφιακού λογισμικού Kidspiration αξίζει να σημειωθεί ότι τα περισσότερα παιδιά ήταν ενημερωμένα και εξοικειωμένα σχετικά με τη χρήση του ποντικιού και τη λειτουργία αυτού, αλλά και με τη λειτουργία του ηλεκτρονικού υπολογιστή γενικότερα.. Εντούτοις, για τα παιδιά τα οποία δεν ήταν εξοικειωμένα με τη χρήση του υπολογιστή, ήταν σημαντική η χρήση αυτού, καθόσον ήρθαν σε μια πρώτη επαφή και ως ένα βαθμό έμαθαν να τον χειρίζονται. Τέλος, τόσο τα παιδιά κατανόησαν ότι η τεχνολογία παίζει βοηθητικό και υποστηρικτικό ρόλο και αποτελεί έναν νέο τρόπο μάθησης, αλλά και η διδακτική-ερευνητική ομάδα διαπίστωσε ότι σημαντικό ρόλο στη μάθηση παίζει η κατάλληλη μέθοδος, τα παραδείγματα και τα υλικά που θα χρησιμοποιηθούν.
Μαθηματική έννοια και δεξιότητες: Είναι σε όλους γνωστό ότι η διαίρεση είναι μια καθόλα σύνθετη πράξη. Ορίζεται σήμερα αυστηρά με την βοήθεια του πολλαπλασιασμού, ως αντίστροφη διαδικασία από τον πολλαπλασιασμό. Αυτός όμως ο ορισμός αφορά διδασκαλία η οποία απευθύνεται σε ανώτερες από το νηπιαγωγείο βαθμίδες εκπαίδευσης. Επίσης, η διαίρεση μπορεί να οριστεί και ως διαδοχική αφαίρεση, για παράδειγμα τα παιδιά μοιράζουν δίκαια, είτε αφαιρώντας διαδοχικά ανά 1 είτε ανά 2, ανά 3 κ.λ.π. (βλ. Εξαρχάκος Θεοδόσης: Διδακτική των μαθηματικών και βιβλίο δασκάλου, μαθηματικά β΄ δημοτικού).
(α/β = α Χ 1/β)
Επίσης, ο αυστηρός ορισμός της Ευκλείδιας διαίρεσης δεν δύναται να χρησιμοποιηθεί στα παιδιά της προσχολικής ηλικίας καθόσον δεν είναι προσιτός σε αυτά και περιέχει δυσκολία κατανόησης. Ακόμη θα έλεγε κανείς ότι δεν μπορεί να χρησιμοποιηθεί και στις πρώτες τάξεις του δημοτικού σχολείου.
Στην ευκλείδια διαίρεση: αν υ=0 τότε Δ=δ.π (τέλεια διαίρεση)
Αν υ διαφορετικό από το 0 τότε Δ = δΧπ+υ (ατελής διαίρεση).
Όπου Δ=διαιρετέος, δ=διαιρέτης, υ=υπόλοιπο, π=πηλίκο
Στη διαίρεση ο πρώτος αριθμός λέγεται διαιρετέος και ο δεύτερος διαιρέτης. Το αποτέλεσμα της διαίρεσης λέγεται πηλίκο. Αν ο διαιρέτης δεν διαιρείται ακριβώς με τον διαιρετέο τότε στο αριστερό μέρος της διαίρεσης μένει το υπόλοιπο. Ειδικότερα, στην αριθμητική η διαίρεση είναι η πράξη που αποβλέπει στο μερισμό ενός αριθμού που λέγεται διαιρετέος, σε τόσα ίσα μέρη όσα δηλώνουν οι μονάδες που υπάρχουν σε ένα άλλο αριθμό, που λέγεται διαιρέτης. Αν ο διαιρετέος περιέχει το διαιρέτη ακριβώς, ορισμένες φορές μετά δηλαδή τον πολλαπλασιασμό πηλίκου και διαιρέτη παίρνουμε το διαιρετέο, τότε η διαίρεση είναι ακριβής ή τέλεια. Μπορεί όμως ο διαιρετέος να μην περιέχει το διαιρέτη κατά έναν ακριβή αριθμό φορών, και προκύπτουν αδιαίρετες μονάδες, ο αριθμός των οποίων αποκαλείται υπόλοιπο της διαίρεσης και η διαίρεση ατελής. Το υπόλοιπο είναι πάντα μικρότερο από το διαιρέτη. Στις πρώτες τάξεις του δημοτικού σχολείου και στο νηπιαγωγείο προτιμάται η διδασκαλία της έννοιας της διαίρεσης ως: α) διαίρεση μερισμού και β) ως διαίρεση μέτρησης. Όταν μετρούμε πόσες φορές θα πάρουμε ένα αριθμό για να φτιάξουμε έναν άλλο, τότε κάνουμε διαίρεση μέτρησης. Στη διαίρεση μέτρησης οι αριθμοί είναι ομοειδείς, δηλαδή φανερώνουν το ίδιο πράγμα.
Διαίρεση μερισμού υπάρχει όταν μια ποσότητα μοιράζεται ισόποσα σε ν μικρότερα κομμάτια. Αυτή η έννοια έχει άμεση πρόσληψη από τις νοητικές δυνατότητες των παιδιών και συνάδει με το ηλικιακό και αναπτυξιακό επίπεδο των παιδιών προσχολικής ηλικίας. Θεωρείται αυτή η εργασία ως έλεγχος αυτής της δυνατότητας πρόσληψης εκ μέρους των παιδιών. Αν δηλαδή αυτή η δοκιμασία επιτύχει, τότε τα παιδιά θα έχουν αποκτήσει μια πρώτη άποψη για τη σύνθετη έννοια της διαίρεσης, την οποία θα αξιοποιήσουν στο μέλλον. Επιπλέον μέσα από τις σχεδιασθείσες δραστηριότητες, οι οποίες αναφέρονται αναλυτικά σε αυτήν την εργασία, τα παιδιά καλούνται να παρατηρήσουν πότε είναι μια διαίρεση τελεία και πότε ατελής. Δηλαδή πότε σε μια διαίρεση μερισμού δεν υπάρχει και πότε υπάρχει υπόλοιπο.
Η έννοια της διαίρεσης υπό αυτήν την έννοια είναι μια έννοια πάρα πολύ οικεία στα παιδιά. Τα παιδιά μέσα από τις καθημερινές τους δραστηριότητες τόσο στο χώρο του σπιτιού όσο και στο χώρο του σχολείου καλούνται να πραγματοποιούν διαίρεση μερισμού, καθόσον μοιράζονται διάφορα αντικείμενα όπως παιχνίδια, υλικά για διάφορες δραστηριότητες και άλλα. Είναι επίσης η διαίρεση μερισμού μια αυθόρμητη διαδικασία στην οποία εμπλέκονται τα παιδιά, προκειμένου να διατηρηθεί μια ισορροπία η οποία διέπει τις μεταξύ τους σχέσεις. Οι δραστηριότητες διαίρεσης μερισμού στοχεύουν στην άσκηση των παιδιών στην επίλυση προβλημάτων διαίρεσης, στη διατύπωση προβλέψεων και επαλήθευση αυτών των προβλέψεων από τα ίδια τα παιδιά, στην ανάπτυξη επιχειρηματολογίας των θέσεών τους και των απόψεών τους, στην εκμάθηση του τρόπου επίλυσης προβλημάτων και οργάνωσης της σκέψης και της γνώσης των.
Αξίζει επίσης να σημειωθεί ότι ενώ στο δημοτικό σχολείο αλλά και στις επόμενες βαθμίδες της εκπαίδευσης η έννοια της διαίρεσης έπεται της έννοιας του πολλαπλασιασμού, ιστορικά όμως η διαίρεση μάλλον προηγείται του πολλαπλασιασμού, καθόσον για παράδειγμα η διαίρεση προέκυψε στα παλιά χρόνια από την ανάγκη του πατέρα να μοιράζει για παράδειγμα τα υπάρχοντά του (ζώα, ακίνητα, αντικείμενα) εξίσου στα παιδιά του.
Τέλος, ο Οδηγός Νηπιαγωγού του Υπουργείου παιδείας, στον οποίο κατά κύριο λόγο βασίζονται οι εκπαιδευτικοί των παιδιών προσχολικής ηλικίας, προκειμένου να πραγματοποιήσουν εκπαιδευτικούς σχεδιασμούς και να σχεδιάσουν δημιουργικά περιβάλλοντα μάθησης, δε δίνει ιδιαίτερη έμφαση στο πώς μπορούν τα παιδιά προσχολικής ηλικίας να αναπτύξουν την έννοια της διαίρεσης αλλά και να τη συνδέσουν βιωματικά με οικεία στα παιδιά περιβάλλοντα. Ενδεικτικά προτείνει κάποιες δραστηριότητες σχετικές με τη διαίρεση (μοίρασμα). Είναι βέβαια θετικό το γεγονός ότι προτρέπει τον εκπαιδευτικό να εντάξει τα παιδιά σε οικεία για αυτά πλαίσια (παιχνίδια, ιστοριούλες), προκειμένου να αναπτύξει μια δραστηριότητα διαίρεσης μερισμού. Ωστόσο, αν και αναφέρει την χρήση της τεχνολογίας ως σημαντική προκειμένου να βοηθήσει τα παιδιά να συνδέσουν τη μάθηση που πραγματοποιείται στο σχολείο με τις μαθηματικές εμπειρίες που βιώνουν εκτός σχολείου, στον πραγματικό δηλαδή κόσμο, δεν αναφέρει συγκεκριμένα παραδείγματα και τρόπους χρήσης της τεχνολογίας σχετικά με τη διαίρεση μερισμού.
Το λογισμικό που επιλέξαμε είναι το kidspiration. Το συγκεκριμένο λογισμικό επιλέχθηκε γιατί βρίσκεται στην κατηγορία ψηφιακού υλικού ανοιχτού περιβάλλοντος, δηλαδή δίνει την δυνατότητα στον χρήστη να κινηθεί και να δημιουργεί ελεύθερα, με αποτέλεσμα να λειτουργεί ο καθένας βάσει των δικών του προσωπικών γνώσεων και προηγούμενων εμπειριών. Επίσης, το λογισμικό αυτό έχει έναν μεγάλο αριθμό λειτουργιών, με τα οποία ο διδάσκων μπορεί να δημιουργήσει πολλές δραστηριότητες με διαφορετικά πλαίσια. Αυτό συνεπάγεται ότι ο διδάσκων μπορεί να προσαρμόσει τις δραστηριότητες στις ανάγκες τόσο των παιδιών όσο και του γνωστικού αντικειμένου που θέλει να διδάξει. Οι δεξιότητες που απαιτούνται για τις εφαρμογές που σχεδιάστηκαν είναι απλές και το μόνο που χρειάζεται να κάνει ο μαθητής είναι να σύρει με το ποντίκι το αντικείμενο που θα του ζητηθεί στην ανάλογη θέση. Για το λόγο αυτό η εξάσκηση που απαιτείται είναι σχεδόν μηδαμινή. Χρειάζεται μόνο μια λεπτή κινητικότητα του χεριού, την οποία το νήπιο μπορεί να την αποκτήσει πολύ εύκολα και γρήγορα. Όπως αναφέρθηκε και παραπάνω, χάρη στο ότι το λογισμικό μας είναι ανοιχτού περιβάλλοντος, ο κάθε μαθητής μπορεί να χρησιμοποιήσει διαφορετική διαδικασία για την επίλυση του προβλήματος, δίνοντας όμως στο τέλος την μοναδική σωστή απάντηση. Έτσι, για την πράξη της διαίρεσης που μας αφορά, το κάθε νήπιο είναι ελεύθερο να μοιράσει τα διάφορα αντικείμενα όπως το ίδιο ξέρει και μπορεί, αφού έτσι και αλλιώς η διαδικασία του μοιράσματος και στην πραγματικότητα έχει πολλές επιλογές στο να γίνει, δεν είναι δηλαδή μονόδρομη.
Δραστηριότητα 1η (διάρκεια 30’).
Αρχικά η διδασκαλία μας θα ξεκινήσει με μια συζήτηση που θα γίνει μεταξύ μιας γαντόκουκλας, τον Αρχιμήδη και την ολομέλεια της τάξης. Ο Αρχιμήδης θα συστηθεί στα παιδιά και θα προσπαθήσει μέσα από κάποιες ερωτήσεις να μάθει ποια είναι η σχέση των παιδιών με τα μαθηματικά και αν γνωρίζουν την πράξη της διαίρεσης.Τα παιδιά είναι συγκεντρωμένα στην γωνιά της παρεούλας όταν τους παρουσιάζεται ο Αρχιμήδης υπό τη μορφή γαντόκουκλας και αναπτύσσεται μεταξύ τους ένας άμεσος διάλογος. Ο Αρχιμήδης θέλει τη βοήθεια των παιδιών προκειμένου να τους μοιράσει δέκα τέσσερις μαρκαδόρους. (Τα παιδιά είναι δέκα τρία.) Τι θα γίνει λοιπόν με τον 14° μαρκαδόρο; Και πόσους μαρκαδόρους θα πάρουν τελικά τα παιδιά;
Στην πράξη: Ο Αρχιμήδης αφού συστήθηκε στα παιδιά, τα οποία ενθουσιάστηκαν με την γνωριμία μαζί του, τους ρώτησε ποιο παιδάκι θα τον βοηθούσε προκειμένου να μοιράσει τους μαρκαδόρους που είχε μαζί του κα αυτό γιατί ο ίδιος αδυνατούσε να τους μοιράσει επειδή είχε πλέον γεράσει. Όλα τα παιδιά προθυμοποιήθηκαν να τον βοηθήσουν. Αυτός όμως επέλεξε ένα παιδί, το οποίο μέτρησε με την σειρά τα παιδιά, τα οποία στο σύνολο ήταν δέκα τρεις. Ό Αρχιμήδης έδειξε χαρούμενος και συνεχάρη τα παιδιά που του έδειξαν ότι ήξεραν να μετρούν. Στην συνέχεια διάλεξε ένα άλλο παιδί προκειμένου να μοιράσει τους μαρκαδόρους. Το παιδί αφού τους μέτρησε, οι οποίοι αναφέρθηκε και παραπάνω στο σύνολο ήταν δέκα τέσσερις, τους μοίρασε στα παιδιά. Προτού μοιραστούν οι μαρκαδόροι ο Αρχιμήδης απευθυνόμενος στα παιδιά εξέφρασε μερικές απορίες όπως: θα φτάσουν για όλα τα παιδιά; θα περισσέψει κάποιος; Οι απαντήσεις των παιδιών ξάφνιασαν ευχάριστα τον Αρχιμήδη όπου αφού τους ευχαρίστησε για την βοήθεια που του πρόσφεραν έφυγε από την παρέα τους.
Στην συνέχεια τα παιδιά, προκειμένου να επιτευχθεί η διαδικασία της αξιολόγησης μεταφέρθηκαν στα τραπεζάκια τους όπου μοιράστηκε στο κάθε παιδί από ένα φύλλο εργασίας. Τα παιδιά, ατομικά, καλούνταν να απαντήσουν στα εξής: Μοίρασε τα μπαλόνια στα παιδιά. Το κάθε παιδί θα πάρει τόσα, όσα και το άλλο. Α) Πόσα είναι όλα τα μπαλόνια; Β) Πόσα είναι τα παιδιά; Γ) Πόσα μπαλόνια θα πάρει το κάθε παιδί; Εφόσον μοιράστηκαν τα φύλλα εργασίας στα παιδιά ακολούθησε συζήτηση μαζί τους σχετικά με το τι έπρεπε να γράψουν, όπως ότι ο αριθμός από τα μπαλόνια πρέπει να γραφτεί στην πρώτη γραμμή. Μερικά από αυτά εξέφρασαν διάφορες απορίες όπως: πώς θα μοιραστούν τα μπαλόνια ή τι θα γίνει με τα μπαλόνια που περισσεύουν; Όμως οι παραπάνω απορίες τους γρήγορα επιλύθηκαν και τα παιδιά δεν αντιμετώπισαν κάποιο άλλο πρόβλημα.
Φώτο : γαντόκουκλα «Αρχιμήδης»

Φωτό: Το παιδί μετράει τους μαρκαδόρους που του έδωσε ο «Αρχιμήδης»

Φώτο: το παιδί μοιράζει τους μαρκαδόρους στα υπόλοιπα παιδιά της τάξης

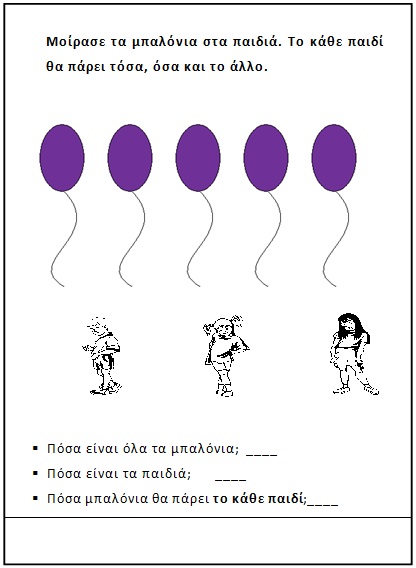
Φώτο : τα παιδιά συμπληρώνουν το φύλλο εργασίας

Στόχος : Να αντλήσουμε πληροφορίες για τις εμπειρίες και γνώσεις των παιδιών πάνω στα μαθηματικά και ιδιαίτερα στη διαίρεση- μοίρασμα. Να έρθουν τα παιδιά σε μια πρώτη επαφή με την πράξη της διαίρεσης και πιο συγκεκριμένα της ατελής διαίρεσης. Να παρατηρήσουν ότι σε κάποιες περιπτώσεις μοιρασιάς, ανάλογα με τον αριθμό των αντικειμένων, υπάρχει κάτι που περισσεύει.
Υλικά: Μαρκαδόροι.
Δραστηριότητα 2η (διάρκεια 30’).
Αφού συγκεντρωθεί η ολομέλεια στην γωνιά της παρεούλας, οι φοιτήτριες ζητάνε κάθε φορά από ένα παιδί να μοιράσει φρούτα σε κάποια καφάσια. Ο αριθμός και των φρούτων αλλά και των καφασιών κάθε φορά αλλάζει. Πιο συγκεκριμένα: Το πρώτο παιδί μοιράζει δυο φρούτα σε δυο καφάσια. Το δεύτερο παιδί μοιράζει δυο φρούτα σε τρία καφάσια. Το τρίτο παιδί θα μοιράζει τέσσερα φρούτα σε δυο καφάσια. Το τέταρτο παιδί μοιράζει τέσσερα φρούτα σε τρία καφάσια. Το πέμπτο παιδί μοιράζει τέσσερα φρούτα σε τέσσερα καφάσια. Το έκτο παιδί μοιράζει έξι φρούτα σε δυο καφάσια. Το έβδομο παιδί μοιράζει έξι φρούτα σε τρία καφάσια. Το όγδοο παιδί μοιράζει έξι φρούτα σε τέσσερα καφάσια. Το ένατο παιδί μοιράζει οκτώ φρούτα σε δυο καφάσια. Το δέκατο παιδί μοιράζει οκτώ φρούτα σε τρία καφάσια. Το ενδέκατο παιδί μοιράζει οκτώ φρούτα σε τέσσερα καφάσια. Το δωδέκατο παιδί μοιράζει δέκα φρούτα σε δυο καφάσια. Το δέκατο τρίτο παιδί μοιράζει δέκα φρούτα σε τρία καφάσια. Το δέκατο τέταρτο μοιράζει δέκα φρούτα σε τέσσερα καφάσια. Μετά από κάθε ενέργεια του παιδιού παρατηρούν το αποτέλεσμα που προκύπτει ώστε να κατανοήσουν ότι το αποτέλεσμα διαφοροποιείται όταν μένει σταθερός ο αριθμός των φρούτων αλλά αλλάζει ο αριθμός των καφασιών. Στο τέλος της διαδικασίας ακολουθεί συζήτηση με τα παιδιά για το πώς μοιράστηκαν τα φρούτα στα καφάσια. Τέλος, μοιράζουμε στα παιδιά από ένα φύλλο αξιολόγησης, στο οποίο πρέπει να κυκλώσουν την σωστή απάντηση, στο πρόβλημα «Έχουμε έξι μήλα και θέλουμε να τα μοιράσουμε σε δυο καλάθια. Βρες σε ποιο καλάθι έχουμε μοιράσει σωστά τα μήλα.»
Στην πράξη: Συμμετείχαν ξεχωριστά όλα τα παιδιά δίνοντας την ευκαιρία να χρησιμοποιήσουν όλοι/ες το χειραπτικό υλικό που είχαν στη διάθεσή τους και να μοιράσουν αντικείμενα ώστε να κατανοήσουν μέσα από βιωματικό τρόπο την έννοια της τέλειας και ατελής διαίρεσης. Τα παιδιά μοίραζαν αντικείμενα διαφορετικών κάθε φορά ποσοτήτων, ώστε να παρατηρήσουν πως στη διαίρεση είναι δυνατόν να υπάρξει υπόλοιπο δηλαδή να μείνουν πράγματα αλλά και να μη μείνουν, ώστε να εξοικειωθούν με την τέλεια και ατελή διαίρεση. Ως προς τον τρόπο μοιράσματος παρατηρήθηκαν παραλλαγές. Κάποια παιδιά έβαζαν για παράδειγμα τρία φρούτα σε κάθε καφάσι και στο τέλος συνειδητοποιούσαν ότι όλα τα καφάσια είχαν ίσο αριθμό, ενώ κάποια άλλα τοποθετούσαν τα φρούτα ένα – ένα στα καφάσια. Τα περισσότερα όμως είχαν ήδη σκεφτεί την πράξη του μοιράσματος, ανακοίνωναν το αποτέλεσμα και την εφάρμοζαν στην πράξη ώστε να επιβεβαιωθούν. Σε κάποιες περιπτώσεις όταν προέκυπτε υπόλοιπο το μοίρασμα όπως γινόταν από τα παιδιά δεν ήταν ισόποσο. Δηλαδή το υπόλοιπο τοποθετούνταν σε ένα καφάσι με αποτέλεσμα αυτό να έχει περισσότερα φρούτα από τα υπόλοιπα. Με κατάλληλη παρέμβαση της νηπιαγωγού, τα παιδιά είτε μοιράζοντας ξανά από την αρχή τα αντικείμενα, είτε μέσα από την πράξη της αφαίρεσης με την οποία ασχολούνταν το διάστημα αυτό, αφαιρούσαν ένα – ένα τα φρούτα από το καφάσι στο οποίο πλεόναζαν ώσπου να επέλθει η ισότητα. Έτσι μοίραζαν τελικά την ποσότητα των αντικειμένων ισόποσα. Αυτό συνέβη γιατί δεν είχαν ακόμη κατανοήσει πως κατά τη διαδικασία του μοιράσματος , προκειμένου αυτό να γίνει ισόποσα, είναι δυνατόν να υπάρξει υπόλοιπο. Δεν είχαν δηλαδή γνωρίσει την έννοια του υπόλοιπου. Όμως μέσα από την επανάληψη και την παρατήρηση της πράξης κάθε παιδιού κατανόησαν την έννοια της ατελής διαίρεσης και του υπολοίπου αφήνοντάς το στην άκρη όταν αυτό προέκυπτε.
Φώτο : το παιδί μοιράζει οκτώ φρούτα σε τέσσερα καφασάκια

Φώτο : το παιδί μοιράζει δέκα φρούτα σε τρία καφασάκια

Φώτο : το παιδί διορθώνει το λάθος και μοιράζει σωστά τα δέκα φρούτα στα τρία καφασάκια


Υλικά: Πλαστικά φρούτα και ξύλινα καφάσια.
Στόχος: Να εξοικειωθούν τα παιδιά με την τέλεια και την ατελή διαίρεση. Να σκεφτούν τι θα κάνουν στην περίπτωση που τα φρούτα και τα καφάσια δε βρίσκονται σε πλήρη αντιστοιχία, δηλαδή όταν υπάρχει υπόλοιπο.
3ⁿ Δραστηριότητα (35' λεπτα).
Τα παιδιά με την βοήθεια των φοιτητριών χωρίζονται σε ομάδες των δύο ατόμων και η κάθε ομάδα κάθεται μπροστά από έναν υπολογιστή. Το κάθε παιδί καλείται να κάνει μια εφαρμογή στο λογισμικό το οποίο έχουμε επιλέξει. Οι εφαρμογές που έχουν σχεδιαστεί για την δραστηριότητα είναι δύο, έτσι το κάθε παιδί της κάθε ομάδας, θα λύσει και διαφορετικό πρόβλημα. Το πρώτο πρόβλημα ονομάζεται «Η γιαγιά Μαρία». Στην συγκεκριμένη εφαρμογή το παιδί πρέπει να βοηθήσει την γιαγιά Μαρία να μοιράσει τις έξι φράουλες που έχει, στα καλαθάκια των δύο εγγονών της. Το ζητούμενο είναι το παιδί να πει πόσες φράουλες τελικά θα έχει στο καλάθι της η κάθε εγγονή. Το δεύτερο πρόβλημα ονομάζεται «Τα τέσσερα γουρουνάκια». Σε αυτή την εφαρμογή το παιδί καλείται να μοιράσει τα έξι μήλα που υπάρχουν στα τέσσερα γουρουνάκια και στο τέλος να βρει πόσα μήλα θα φάει το κάθε γουρουνάκι. Το πρόβλημα αυτό είναι ατελής διαίρεσης και για το λόγο αυτό το παιδί στο τέλος θα παρατηρήσει ότι κάποια μήλα θα περισσέψουν.Και οι δύο αυτές εφαρμογές δεν έχουν έναν συγκεκριμένο τρόπο επίλυσης. Το κάθε παιδί θα μπορέσει να εργαστεί όπως θέλει.
Τα παιδιά ακολουθώντας τις οδηγίες μας δεν αντιμετώπισαν ιδιαίτερα προβλήματα. Βέβαια θα πρέπει να ληφθεί υπ’ όψιν ότι τα περισσότερα έδειχναν εξοικειωμένα με τον ηλεκτρονικό υπολογιστή. Τα περισσότερα παιδιά έβρισκαν αμέσως τις απαντήσεις στα παραπάνω δυο ερωτήματα και αυτό που έπρεπε να κάνουν ήταν να τις υλοποιήσουν χρησιμοποιώντας τον υπολογιστή. Μερικά απ’ αυτά δεν ήταν τόσο πολύ εξοικειωμένα με αυτόν και δυσκολεύονταν να “πιάσουν” με το ποντίκι του υπολογιστή τις φράουλες και να τις βάλουν μέσα στα καλάθια ή άλλες φορές τοποθετούσαν την μια φράουλα πάνω στην άλλη. Επίσης κάποια απ αυτά δεν μπορούσαν να τραβήξουν την γραμμή, η οποία θα έδειχνε πόσες φράουλες θα πάρει το κάθε γουρουνάκι. Δηλαδή ενώ τις περισσότερες φορές οι απαντήσεις των παιδιών στα προβλήματα ήταν σωστές όταν πήγαιναν να τις εφαρμόσουν στον υπολογιστή δυσκολεύονταν. Όμως θα πρέπει να σημειωθεί ότι οι δυσκολίες που αντιμετωπίσαμε δεν μας δημιούργησαν κάποιο ιδιαίτερο ως προς την συνέχιση και την υλοποίηση της δραστηριότητας μας. Τέλος τα παιδιά μετά το πέρας της δραστηριότητας εκτός του ότι κάποια απ αυτά ήρθαν σε πρώτη επαφή με τον υπολογιστή, έμαθαν να επιλύουν προβλήματα σχετικά με την τέλεια και την ατελής διαίρεση και με την βοήθεια της τεχνολογίας.

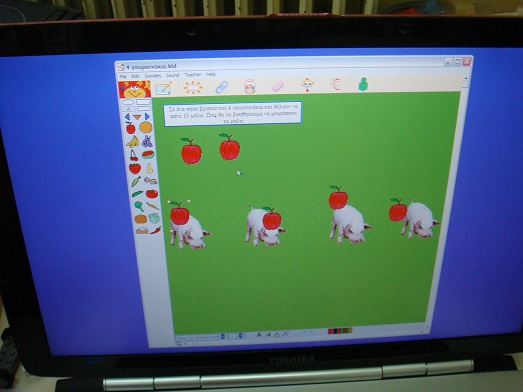
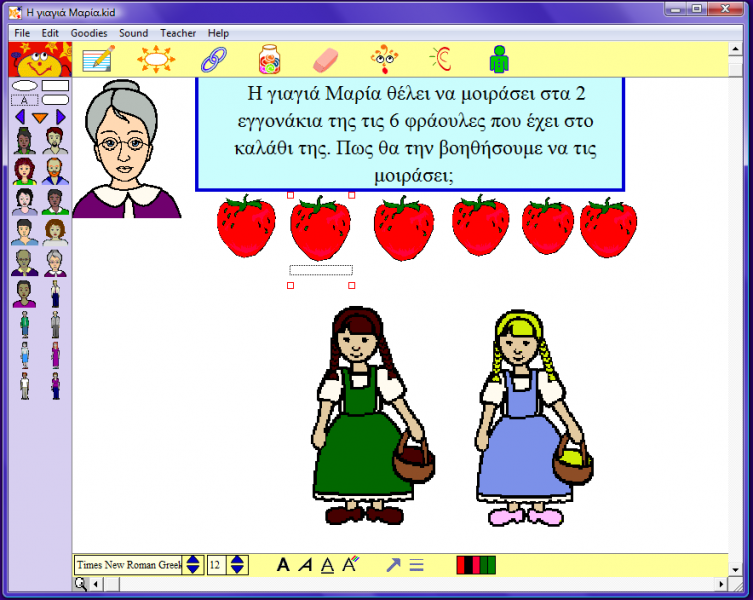
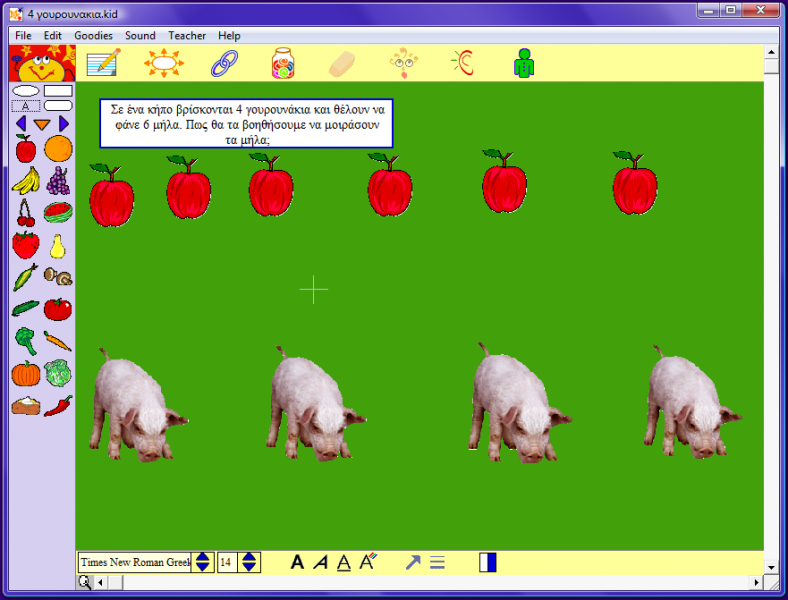
Υλικά : Δύο υπολογιστές, ψηφιακό λογισμικό kidspiration.
Στόχος : Να έρθουν σε επαφή με την τεχνολογία και να την συνδυάσουν με τα μαθηματικά. Να εφαρμόσουν μέσα από το συγκεκριμένο λογισμικό τη πράξη της διαίρεσης. Να παρατηρήσουν ότι σε κάποιες περιπτώσεις υπάρχει υπόλοιπο, δηλαδή ότι κάτι περισσεύει.
Μάθηση και Δράσεις παιδιών: Με βάση τους διδακτικούς στόχους που έχει θέσει η διδακτική μας παρέμβαση προσδοκούμε από τα παιδιά να εργαστούν ατομικά, είτε στις δραστηριότητες με το χειραπτικό υλικό, είτε στις δραστηριότητες με το ψηφιακό λογισμικό. Σε περιπτώσεις λάθους ή δυσκολιών, το παιδί μπορεί να ζητήσει τη βοήθεια από την υπόλοιπη ομάδα. Για να το πετύχουμε αυτό, κάθε μας δραστηριότητα έχει σχεδιαστεί έτσι, ώστε κάθε παιδί ξεχωριστά να πάρει μέρος σε αυτές. Για παράδειγμα στη δραστηριότητα με τα φρούτα και τα καφασάκια, σε κάθε παιδί με τη σειρά, θα ζητηθεί να μοιράσει διαφορετικές ποσότητες φρούτων σε διαφορετικές ποσότητες καφασιών. Επίσης, στις δραστηριότητες με το ψηφιακό λογισμικό, το κάθε παιδί θα διαλέξει και θα εργαστεί σε μία από τις δυο σχεδιασμένες μας δραστηριότητες μόνο του. Είναι σημαντικό όλες οι δραστηριότητες μας να γίνουν ατομικά, για να κατανοήσουν τα παιδιά ότι ανάλογα με τους αριθμούς, αλλάζει το αποτέλεσμα και σε κάποιες φορές μένει υπόλοιπο και άλλες όχι.
Εφαρμογή στην πράξη μιας διδακτικής παρέμβασης: Θα πρέπει να σημειωθεί ότι πραγματοποιήθηκαν δυο άτυπες συνεντεύξεις προκειμένου να έρθουν τα παιδιά σε μια πρώτη επαφή με την διαίρεση. Η πρώτη πραγματοποιήθηκε λίγο πριν την περίοδο των Χριστουγέννων και η επόμενη μετά το Πάσχα και συγκεκριμένα στις 19-4-2010. Αυτό συνέβη εξαιτίας των ανειλημμένων μας υποχρεώσεων που δεν μας επέτρεψαν να πραγματοποιήσουμε τις δραστηριότητες μας στο πλαίσιο της πρώτης μας άτυπης συνέντευξης με τα παιδιά. Γι’ αυτό το λόγο κρίθηκε σκόπιμο προτού προβούμε στην υλοποίηση των δραστηριοτήτων να οργανωθεί και μια δεύτερη άτυπη συνέντευξη προκειμένου να διευκολυνθεί η επικοινωνία μας με τα παιδιά. Και στις δυο επισκέψεις που πραγματοποιήθηκαν, στο πλαίσιο πάντα της συνέντευξης, όπου στην ουσία επρόκειτο για μια πρώτη γνωριμία με τα παιδιά, μας δόθηκε η ευκαιρία εκτός από τα παιδιά να μάθουμε από τη νηπιαγωγό του τμήματος το τι είχαν διδαχτεί. Η νηπιαγωγός μέχρι και την περίοδο των Χριστουγέννων μας πληροφόρησε ότι δίδασκε τα σχήματα, όπως το τρίγωνο, το ορθογώνιο, το τετράγωνο και τον κύκλο. Επίσης, μέχρι τότε είχε διδάξει τη διάταξη της ποσότητας χρησιμοποιώντας ως εποπτικό υλικό λάδι και κίτρινο υγρό. Στόχοι της ήταν η εξοικείωση των παιδιών με τα σχήματα, να εισάγει τα παιδιά στην έννοια της συμμετρίας, χρησιμοποιώντας χριστουγεννιάτικες μπάλες και να εξοικειωθούν με την έννοια της σειροθέτησης. Η νηπιαγωγός στο μέλλον έχει σκοπό να διδάξει την αντιστοίχιση, το ύψος, τη διάταξη και κάποιες μαθηματικές πράξεις. Ειδικότερα, την έννοια του χαμηλού, του ψηλού, του μικρότερου, του μεγαλύτερου, της πρόσθεσης, της αφαίρεσης. Η μέθοδος που πρόκειται να χρησιμοποιήσει είναι η βιωματική, μέσα από διάφορα υλικά οικεία στα παιδιά. Κατά την δεύτερη επίσκεψη μας στο νηπιαγωγείο διαπιστώθηκε ότι οι γνώσεις των παιδιών πάνω στα μαθηματικά είχαν διευρυνθεί και αυτό γιατί η νηπιαγωγός εισήγαγε τα παιδιά στις έννοιες της πρόσθεσης και της αφαίρεσης. Έτσι διαπιστώσαμε την επέκταση των γνώσεων τους και με βάση αυτές κινηθήκαμε προκειμένου να οργανωθούν οι δραστηριότητες της διαίρεσης.
Γενικά όπως προκύπτει από τις συνεντεύξεις και συζητήσεις με τα παιδιά του νηπιαγωγείου αλλά και από τα φύλλα αξιολόγησης που τους δόθηκαν, δεν προέκυψαν ιδιαίτερες δυσκολίες σε αυτά κατά την εφαρμογή των δραστηριοτήτων. Από την φάση ακόμη της άτυπης συνέντευξης που πραγματοποιήθηκε μαζί τους, διαφάνηκε πως το επίπεδό τους ήταν αρκετά προχωρημένο στα μαθηματικά και στην έννοια του μοιράσματος, αφού έδιναν επιτυχείς απαντήσεις σε απλά προβλήματα διαίρεσης που τους τέθηκαν, βασιζόμενα μάλιστα σε νοερούς μόνο υπολογισμούς. Σε αυτά οδηγήθηκαν μέσα από τις καθημερινές τους εμπειρίες και μέσα από μορφή άτυπης εκπαίδευσης, αφού έως εκείνη τη στιγμή η νηπιαγωγός δεν είχε ασχοληθεί με το θέμα της διαίρεσης – μοίρασμα. Από τα παιδιά προέκυψαν και κάποιες έξυπνες και προχωρημένες λύσεις. Για παράδειγμα, στην περίπτωση μοιράσματος έξι καρότων σε τέσσερα λαγουδάκια, για τα δύο καρότα που περισσεύουν προτάθηκε από κάποιο παιδί να κοπούν στη μέση, δηλαδή να γίνουν τέσσερα κομμάτια και να πάρουν από ένα και τα τέσσερα λαγουδάκια δηλαδή κάθε λαγουδάκι από μισό καρότο ακόμα (υπόλοιπο). Επομένως μαζί με το προηγούμενο καρότο που πήρε το κάθε λαγουδάκι, σύνολο 1,5 καρότα το καθένα. 6:4=1,5. Το παιδί έκανε δηλαδή στο μυαλό του τη διαίρεση και στη συνέχεια μοίρασε και το υπόλοιπο της διαίρεσης! Επίσης ένα δεύτερο έξυπνο επεισόδιο παρατηρήθηκε όταν ζητήθηκε να πούνε πως θα μοιραστούν τρία καρότα σε δύο λαγουδάκια, όπου είχανε την ευφυή παρέμβαση να προσθέσουμε ένα καρότο ακόμη, ώστε η διαίρεση να είναι τέλεια.
Φώτο : το παιδί μοιράζει έξι καρότα σε δυο λαγουδάκια

Για την καταγραφή της διδακτικής παρέμβασης χρησιμοποιήθηκαν videocamera, φωτογραφική μηχανή και συσκευή ηχογράφησης.
Η διδακτική μας παρέμβαση έχοντας ως θέμα τη διαίρεση – μοίρασμα, έδωσε την ευκαιρία στα παιδιά του 26ου νηπιαγωγείου Βόλου να ασχοληθούν και να πειραματιστούν με την έννοια αυτή. Η έννοια της διαίρεσης – μοίρασμα αποτελεί ένα εργαλείο για την επίλυση προβλημάτων τα οποία συναντά κανείς στην καθημερινή του ζωή. Τέτοια προβλήματα επιλύουν όχι μόνο οι ενήλικες χρησιμοποιώντας αριθμητικά ποσά και σύμβολα της διαίρεσης, αλλά και παιδιά μικρής ηλικίας καθώς καλούνται να μοιράσουν διάφορα αντικείμενα στο χώρο του σχολείου αλλά και έξω από αυτόν, όπως για παράδειγμα μαρκαδόρους, χαρτιά, καραμέλες, βόλους κ.α. Μόλις η νηπιαγωγός αντιληφθεί πως τα νήπια δείχνουν κάποιο ενδιαφέρον για τη διαίρεση ή προκύψει μια αφορμή που μπορεί να οδηγήσει σε τέτοιου είδους δραστηριότητες, καλό θα ήταν να τα αξιοποιήσει. Έχοντας τα νήπια κατανοήσει την έννοια της διαίρεσης θα μπορούν να επιλύουν προβλήματα, να είναι αυτόνομα, να αναπτύξουν τη σκέψη και τη λογική τους.
Στόχος αυτή της διδακτικής παρέμβασης δεν είναι ήταν να μάθουν τα παιδιά της προσχολικής ηλικίας να εκτελούν σωστά πράξεις διαίρεσης αλλά να αποκτήσουν δεξιότητες σχετικές με αυτή την έννοια και το συνδυασμό της με τη χρήση ηλεκτρονικού υπολογιστή, μέσα από κατάλληλες λογισμικές εφαρμογές. Απώτερος σκοπός είναι να αναπτυχθεί και να καλλιεργηθεί η μαθηματική σκέψη των παιδιών, η ικανότητα επίλυσης καθημερινών προβλημάτων με μαθηματικό τρόπο , καθώς επίσης και η εξοικείωση και χρήση νέων τεχνολογιών. Τα παιδιά επεξεργάστηκαν, παρατήρησαν, απαρίθμησαν και μοίρασαν αντικείμενα τόσο με τη χρήση χειραπτικού υλικού όσο και με τη χρήση του ηλεκτρονικού υπολογιστή. Ασχολήθηκαν βιωματικά με την έννοια της διαίρεσης, ξεφεύγοντας από την απομνημόνευση κανόνων.
Η σύγχρονη διδακτική δέχεται πως στα παιδιά μπορείς να διδάξεις οτιδήποτε αρκεί να χρησιμοποιήσεις κατάλληλες μεθόδους, εργαλεία και προσαρμογές. Το δόγμα αυτό επιβεβαιώθηκε με αυτή την εργασία στην οποία μια σύνθετη μαθηματική έννοια, η διαίρεση μερισμού, προσφέρθηκε κατάλληλα στα παιδιά επιτυγχάνοντας έτσι τους στόχους που είχαν τεθεί. Συγκεκριμένα έγινε προσπάθεια να προσεγγίσουν τα παιδιά την έννοια της διαίρεσης στα πλαίσια του νέου διαθεματικού προγράμματος σπουδών που προτείνεται σήμερα για την μάθηση τους.. Έτσι μέσα από παιγνιώδη τρόπο, μέσα από αυτοσχέδιες ιστορίες από τις οποίες ξεπηδούσαν προβλήματα μοιράσματος και μέσα από τη χρήση του ηλεκτρονικού υπολογιστή τα παιδιά καλούνταν να επιλύσουν προβλήματα αυτενεργώντας και διασκεδάζοντας. Μοίρασαν προσφιλή σε αυτά αντικείμενα σε ορισμένο αριθμό υποδοχέων. Η διδακτική ομάδα είχε τη δυνατότητα να μεταβάλλει τον διαιρετέο και διαιρέτη, δίνοντας έτσι την ευκαιρία στα παιδιά να γνωρίσουν την έννοια του υπολοίπου. Αν και μεταξύ των δραστηριοτήτων δεν υπήρξε κάποια συνοχή, αλλά ήταν ανεξάρτητες μεταξύ τους, οι στόχοι επιτεύχθηκαν χωρίς δυσκολίες. Φυσικά οι δραστηριότητες και η παρέμβαση, όπως εκ των υστέρων διαπιστώθηκε, θα μπορούσαν να είχαν οργανωθεί και σχεδιαστεί με περισσότερη φαντασία ενέχοντας και κάποιο βαθμό δυσκολίας που να προβληματίζει και να ενεργοποιεί περισσότερο τη σκέψη των παιδιών. Αυτό γιατί το επίπεδό τους ήταν αρκετά καλό, όπως εξάλλου διαφάνηκε από τις πρώτες επαφές μαζί τους. Θα μπορούσαν δηλαδή να είναι λίγο πιο πολύπλοκες ως προς τον τρόπο παρουσίασή τους και να μην κινούνται όλες στο ίδιο στυλ.
Η εφαρμογή και η εμπλοκή με το ψηφιακό λογισμικό Kidspiration που χρησιμοποιήθηκε, βοήθησε αρχικά τα παιδιά να ασκήσουν την παρατηρητικότητά τους και τους πρόσφερε διαφορετικές δυνατότητες από αυτές που θα είχαν αν έμεναν μόνο στο παραδοσιακό και χειραπτικό υλικό. Για παράδειγμα ο χαρακτήρας των δραστηριοτήτων στα λογισμικά ήταν παιγνιώδης, υπήρχε ποικιλία χρωμάτων, και η διόρθωση λαθών ήταν εύκολη. Έτσι η δραστηριότητα αποκτούσε ενδιαφέρον για τα παιδιά. Επίσης βοήθησε όσα παιδιά δεν ήταν εξοικειωμένα με την χρήση του ηλεκτρονικού υπολογιστή να μάθουν ως ένα βαθμό να τον χειρίζονται. Κατανόησαν έτσι πως η χρήση της τεχνολογίας μπορεί να αποτελέσει ένα τρόπο μάθησης. Έδωσε την ευκαιρία στα παιδιά να συνεργαστούν, ως ένα βαθμό, αφού αυτά που ήταν περισσότερο εξοικειωμένα με τη χρήση του βοήθησαν τα άλλα. Η χρήση του λογισμικού βοήθησε όχι μόνο τα παιδιά αλλά και τη διδακτική ομάδα ώστε να εστιάσει την προσοχή των παιδιών στον στόχο που είχε τεθεί προς διερεύνηση και διδασκαλία. Επίσης η διδακτική ομάδα διαπίστωσε πόσο σημαντικό ρόλο παίζει η κατάλληλη μέθοδος, τα παραδείγματα και τα υλικά όταν αυτά χρησιμοποιούνται στη μάθηση των παιδιών. Για παράδειγμα στη συγκεκριμένη παρέμβαση το παραμύθι – ιστορία αποτέλεσε πλαίσιο μέσα στο οποίο προσφέρθηκαν νέες γνώσεις και δεξιότητες.
Κλείνοντας αξίζει να σημειωθεί πως η χρήση της ψηφιακής τεχνολογίας στην εκπαίδευση προσφέρει δυνατότητες για τη διδασκαλία πλήθους θεμάτων. Έχει ρόλο βοηθητικό και υποστηρικτικό προκειμένου να επιτευχθούν μαθησιακοί στόχοι αλλά και για να δώσει στα παιδιά την ευκαιρία να προβληματιστούν και να πειραματιστούν.
Βιβλίο δασκάλου, Μαθηματικά Β΄ δημοτικού, ΟΕΔΒ
ΔΕΠΠΣ
Εξαρχάκος Θ., «Διδακτική των μαθηματικών», Ελληνικά Γράμματα
Οδηγός Νηπιαγωγού, ΟΕΔΒ
John A. Van De Walle, Διδάσκοντας μαθηματικά, Επίκεντρο