Δραστηριότητες με Ράβδους Cuisenaire και το Kidspiration
Submitted by ltme on Fri, 05/22/2015 - 11:53Βιογραφία και έργο Cuisenaire (συνεισφορά στη μαθηματική εκπαίδευση)
Ο George Cuisenaire ήταν Βέλγος δάσκαλος δημοτικού σχολείου ο οποίος εφεύρε τα ξυλάκια Cuisenaire για να διδάξει μαθηματικά. Το 1952 έκδωσε το πρώτο του έργο με τίτλο “Numbers in color”. Με τον τρόπο αυτό έδειξε στον κόσμο πως το έργο του μπορεί να χρησιμοποιηθεί για να διδάξει τα πρώιμα στάδια αριθμητικής. Αφορμή όλων αυτών ήταν η αποδοχή ότι το παιδί πρέπει να μάθει και να διδαχθεί , μέσα από την πράξη η οποία θα τον βοηθήσει να αποκτήσει την απαιτούμενη αυτοπεποίθηση. Μέσα από έρευνες ανακάλυψε ότι παιδιά μεταξύ ηλικίας 6-7 ετών που χρησιμοποίησαν τα ξυλάκια απέκτησαν άριστες επιδόσεις στην αριθμητική. Οι παρατηρήσεις του προκάλεσαν ενδιαφέρον και ενθουσιασμό, καθώς επιβεβαιώθηκαν από χιλιάδες δασκάλους σε περισσότερες από 60 χώρες, με αποτέλεσμα να διαδοθούν οι ράβδοι Cuisenaire από δάσκαλο σε δάσκαλο και άρα από σχολείο σε σχολείο. Στη συνέχεια σε συνεργασία με τον Caleb Gattegno η δουλειά του έγινε ευρύτερα γνωστή.
Μαθηματικές δραστηριότητες αριθμών και πράξεων με τις ράβδους Cuisenaire
Οι ράβδοι Cuisenaire χρησιμοποιούνται για την ανάπτυξη της έννοιας του αριθμού, των σχέσεων των αριθμών μεταξύ τους των πράξεων μεταξύ των αριθμών και των κλασματικών εννοιών. Είναι δηλαδή μοντέλα μήκους τα οποία τα παιδιά διαχειρίζονται σε δραστηριότητες σύνθεσης και σύγκρισης μηκών. Οι ράβδοι Cuisenaire έχουν κομμάτια με μήκη 1 έως 10 μετρημένα με βάση τη μικρότερη ράβδο.

Κάθε μήκος είναι διαφορετικού χρώματος για να αναγνωρίζεται εύκολα. Το μοντέλο χρήσης της ράβδου είναι ευέλικτο διαθέτοντας χωριστά χρώματα για συγκρίσεις. Εκτός από δραστηριότητες που στοχεύουν στην ανάπτυξη της έννοιας του αριθμού στις πρώτες τάξεις του δημοτικού (Γεωργιάδου-Καμπουρίδη & Μαρκόπουλος, 2007) οι ράβδοι Cuisenaire μπορούν να χρησιμοποιηθούν ως υποστηρικτικό υλικό για την αντιμετώπιση δυσκολιών των παιδιών σε μεγαλύτερες τάξεις. Είναι σημαντικό τα παιδιά να αντιληφθούν και να αναπτύξουν, μέσα από μία ποικιλία δράσεων, τις σταθερές σχέσεις που συνδέουν τους αριθμούς ως το 10 και στη συνέχεια των δεκάδων ως το 100. Οι σταθερές αυτές σχέσεις, που δεν απομνημονεύονται αλλά σταθεροποιούνται μέσα από τη συστηματική χρήση, αποτελούν τη βάση για κάθε αριθμητική ανάπτυξη.
Αρχές της μεθόδου – μεθόδευση της διδασκαλίας
Με το υλικό Cuisenaire διευκολύνεται το παιδί να κάνει πολλές προκαταρκτικές ασκήσεις, ώστε να κατανοήσει την έννοια του αριθμού και το περιεχόμενο των 4 πράξεων, πριν αρχίσει ν’ ασχολείται με τους νοερούς υπολογισμούς και τα σύμβολα των αριθμών. Έτσι π.χ.
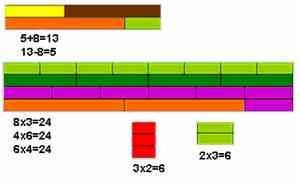
Κόκκινο (2) και κόκκινο (2) έχουν μήκος όσο το μοβ (4).
Μοβ και μοβ έχουν μήκος όσο ένα καφέ (8).
Κίτρινο (5) και κίτρινο (5) έχουν μήκος όσο ένα πορτοκαλί (10).
Ανοιχτό πράσινο (3) και ανοιχτό πράσινο (3) έχουν μήκος όσο το σκούρο πράσινο (6).
Κίτρινο (5) και ανοιχτό πράσινο (3) έχουν μήκος όσο το καφέ (8) κ.λπ.
Η αντίληψη των αριθμών από το 1-10 γίνεται κατανοητή ως μια σύνδεση μηκών και χρωμάτων που αργότερα το παιδί θα διαχειρίζεται ως τα «ζευγάρια του 10».

Οι ράβδοι Cuisenaireως «ζευγάρια του 10»
Με τον τρόπο αυτό, βοηθούνται τα παιδιά να κατακτήσουν το νόημα της πρόσθεσης των αντικειμένων. Με τις ράβδους και πριν μάθουν τα παιδιά τη συμβολική αναπαράσταση των αριθμών, θα κάνουν πολλές αντίστοιχες ασκήσεις για κάθε πράξη, ώστε εύκολα υστέρα να περάσουν στην αφηρημένη και συμβολική διαχείριση αριθμών και πράξεων, να περάσουν δηλαδή από τις ράβδους στους αριθμούς. Έτσι, για παράδειγμα ο αριθμός 10 εκτός από «τα ζευγάρια του 10» μπορεί να αναλυθεί σε πολύ περισσότερα μήκη.

Οι ράβδοι Cuisenaire ως «ομάδες του 10»
Συνδυασμοί και σχέσεις αριθμών μεγαλύτερων του 10
Η συστηματική ενασχόληση με το παραπάνω υλικό διευκολύνει την παρατηρητικότητα του παιδιού, την αυτενέργεια και δημιουργικότητα, την επαλήθευση και την κατανόηση και τελικά το οδηγεί σταδιακά στη μαθηματική σκέψη. Οι φάσεις αυτές της εργασίας συνδέονται μεταξύ τους με τέτοιο τρόπο, ώστε ή παρατήρηση να διευκολύνει την πράξη, τον αριθμητικό υπολογισμό, τον αυτοέλεγχο του παιδιού και την κατανόηση των αριθμητικών πράξεων απ’ το παιδί.
Παρατήρηση
α) Τα χρώματα, συνδεδεμένα όπως είναι σε οικογένειες και όπως αντιπροσωπεύουν διαφόρους αριθμούς το καθένα, ασκούν την παρατηρητικότητα του παιδιού και οδηγούν στη σύνδεση της παρατήρησης με νοερούς υπολογισμούς.
β) Οι διαστάσεις (τα μεγέθη) των ράβδων, όντας διαφορετικές και συμμετρικές, διευκολύνουν το παιδί να σχηματίζει συγχρόνως νοητικές εικόνες και διαφορετικές αντιλήψεις των μεγεθών, χρησιμοποιώντας τις αισθήσεις του όραση και αφή και να κάνει νοητικές συνδέσεις των αισθήσεων με τις νοητικές εικόνες.
γ) Τέλος, ο συνδυασμός χρωμάτων και διαστάσεων, διευκολύνει τη συμβολή όλων των αισθήσεων του παιδιού και την άσκηση της νοητικής του ικανότητος, προετοιμάζοντάς το για την εμφάνιση της αφαιρετικής σκέψης.
Γενικά, η συστηματική ενασχόληση με δραστηριότητες που αξιοποιούν το υλικό αυτό διευκολύνει το παιδί να εξοικειωθεί με τις σχέσεις των μεγεθών, των ποσοτήτων και των αριθμών και το οδηγεί στην απόκτηση νοητικών εικόνων, που οι οποίες θα είναι ακριβείς και θα έχουν διάρκεια (άσκηση στο να απομνημονεύει χρώματα και μεγέθη, με κλειστά μάτια).
Αυτενέργεια και δημιουργικότητα
Με τη χρησιμοποίηση του υλικού αυτού, το παιδί ικανοποιεί την ανάγκη για νοητική αναζήτηση, γιατί το υλικό αυτό υποκινεί το παιδί να εφεύρει αυθόρμητα και ελεύθερα πολλούς και ποικίλους συνδυασμούς, στηριγμένους στις σχέσεις και στις ομάδες των αριθμών. Οι συνδυασμοί αυτοί εφευρίσκονται απ’ το παιδί με ανιχνεύσεις και υποθέσεις που επαληθεύονται απ’ το ίδιο με βάση το υλικό. Η νοητική αυτή αναζήτηση που προκαλεί το υλικό Cuisenaire είναι η καλύτερη μορφή αυτενέργειας καθώς στηρίζει τη δημιουργικότητα μέσα από διαδικασίες πειραματισμού και αυτοέλεγχου.
Επαλήθευση και Κατανόηση
Πρόκειται για την πιο σημαντική φάση της ενασχόλησης του παιδιού με το υλικό αυτό. Το παιδί με τις πολλές του ανιχνεύσεις για τους αριθμητικούς συνδυασμούς που εμπεριέχει το υλικό κάνει υπολογισμούς, εκτιμήσεις αλλά και λάθη, τα όποια όμως διορθώνει το ίδιο, την ίδια στιγμή που τα διαπιστώνει, με τη βοήθεια πάντοτε του συγκεκριμένου υλικού. Ασκώντας με τον τρόπο αυτό τη δημιουργική φαντασία και τους νοερούς υπολογισμούς το παιδί εύκολα προχωρά στην κατανόηση ποσοτήτων και σχέσεων που αφορούν τους αριθμούς και τις πράξεις τους.

Προσπαθώντας για το 27. (8+8+8 ≠27 όπως και 8+8+8+4 ≠27)

Φτιάχνοντας το 27. (8+8+8 + 3 = 27 ή 3 οχτάρια + 3=27)
Μαθηματική σκέψη
Με τη συστηματική χρήση του υλικού αυτού μέσα από δραστηριότητες, το παιδί αναζητά κάθε φορά νέους αριθμητικούς συνδυασμούς για να ικανοποιήσει την έφεση του στην ανακάλυψη νέων σχέσεων και υπολογισμών. Η δράση αυτής της μορφής επάνω στα υλικά το οδηγεί αρχικά στην κατανόηση στην αυτοματοποίηση των διαδικασιών και σταδιακά στη μαθηματική σκέψη.


Αντίληψη των αριθμών 11 ως 20 με τη βοήθεια του υλικού
Γενικά, η μέθοδος εργασίας με το υλικό Cuisenaire, εμφανίζει τα έξης πλεονεκτήματα:
- Διευκολύνει κάθε παιδί να συγκροτεί τη μαθηματική του σκέψη, σύμφωνα με τις ατομικές πνευματικές του δυνατότητες, οι όποιες είναι διαφορετικές στο κάθε παιδί. Με τον τρόπο αυτό το υλικό στηρίζει την ατομική εργασία.
- Ασκεί την παρατηρητικότητα και δημιουργεί σαφείς και μόνιμες οπτικές εικόνες.
- Διευκολύνει την απόκτηση απ’ το παιδί της ιδέας του «όλου», σε συσχετισμό με τα «μέρη», με τις ποικίλες συνθέσεις και αναλύσεις του υλικού.
- Οδηγεί προοδευτικά και συστηματικά το παιδί απ’ τη συγκεκριμένη στην αφαιρετική σκέψη, με το να το συνηθίζει να «βλέπει» με τη σκέψη του ό,τι κάνει στην πράξη με το υλικό, είτε ανιχνεύοντας, είτε επαληθεύοντας τις ανιχνεύσεις του.
- Με την ανάπτυξη και καλλιέργεια της μαθηματικής σκέψης — καλλιέργεια που γίνεται με τη συστηματική χρησιμοποίηση του υλικού απ’ το παιδί και με την ενεργητική συμμετοχή όλων των αισθήσεων του με βάση τις διαστάσεις του υλικού τις σχέσεις των διαστάσεων και των χρωμάτων— το παιδί αναπτύσσει τις ικανότητες της ανάλυσης και της σύνθεσης με το να πραγματοποιεί συνδυασμούς που ξεκινούν απ’ τη δική του εμπειρία. Έτσι, ομαλά και με φυσικό τρόπο, η σκέψη του παιδιού προχωρά από τη διαχείριση αντικειμένων στη μαθηματική σκέψη.
- Το υλικό Cuisenaire κάνει το μάθημα ευχάριστο, ελκυστικό και ζωντανό για το παιδί.
- Η εργασία με το υλικό αυτό νοηματοδοτεί την «έννοια» του αριθμού και επιτρέπει στο παιδί να χρησιμοποιήσει ελεύθερα και άνετα τις προσωπικές του εικόνες για τον αριθμό στην κατανόηση των αριθμητικών υπολογισμών.
- Το υλικό αυτό χτίζει τις γέφυρες που συνδέουν την εργασία του παιδιού πάνω στο συγκεκριμένο μαθηματικό υλικό με τα σύμβολα των αριθμών.
Με λίγα λόγια, το παιδί που χρησιμοποιεί το υλικό αυτό, παρατηρεί, ενεργεί, εφευρίσκει, υπολογίζει και επαληθεύει. Παρατηρεί τον αριθμό στην ουσία του και στην ολότητα του κι όχι αριθμώντας σύμβολα. Παρατηρεί τη σχέση μεταξύ των ίδιων μεγεθών ή χρωμάτων (σχέση ποσού) και μεταξύ διαφορετικών μεγεθών (σχέση μεγέθους). Ενεργεί βάζοντας τα διάφορα ραβδάκια σε συνέχειες και εφευρίσκοντας ελεύθερα όλους τους δυνατούς συνδυασμούς. Εφευρίσκει πειραματικά τη σύνθεση και την ανάλυση κάθε αριθμού. Υπολογίζει δίχως να ξέρει αριθμούς και φθάνει σύντομα στους μαθηματικούς αυτοματισμούς. Ελέγχει και επαληθεύει μόνο του τους υπολογισμούς που έκανε, διορθώνει μόνο του τα λάθη του δουλεύοντας ατομικά ή μέσα στην ομάδα. Εκφράζεται με μαθηματική ακρίβεια, που με άλλον τρόπο είναι δύσκολο να το επιτύχει.
Απαιτούμενα υλικά και μέσα
Για να μπορεί να λειτουργήσει η τάξη με ράβδους Cuisenaire είναι αυτονόητο ότι απαιτούνται τόσες συλλογές από ράβδους όσες και οι ομάδες των παιδιών (π.χ. για μια τάξη 20 παιδιών θα χρειαστούν 5 συλλογές). Ακόμη και στο στάδιο ατομικής εργασίας τα παιδιά μπορούν να χρησιμοποιούν ξυλάκια από την ίδια συλλογή (εικόνα 24). Οι ράβδοι του εμπορίου είναι ξύλινες (ακριβότερες) ή πλαστικές. Το σχολείο μπορεί να προμηθευτεί τις αντίστοιχες ανάλογα με τις οικονομικές του δυνατότητες.

Χρήση υλικού Cuisenaire από δύο παιδιά
Προτεινόμενη οργάνωση της τάξης
Τα παιδιά προτείνεται να λειτουργήσουν αρχικά ατομικά, καθώς εξοικειώνονται με το υλικό και στη συνέχεια εταιρικά καθώς θα χρησιμοποιούν το υλικό για επαλήθευση των λύσεων στις οποίες κατέληξαν. Είναι αυτονόητο πως οι στοιχειώδεις συνεργατικές δεξιότητες πρέπει να έχουν ήδη καλλιεργηθεί ώστε η διαχείριση του υλικού να γίνεται αποτελεσματικά και χωρίς πρόσθετες δυσκολίες από τα παιδιά.
Προαπαιτούμενη γνώση: Τα παιδιά είναι απαραίτητο να έχουν ασχοληθεί και εξασκηθεί στην εκμάθηση της φυσικής ακολουθίας των αριθμών μέχρι το 10 ώστε να προχωρήσουν στην ενασχόληση δραστηριοτήτων με τα ξυλάκια Cuisenaire.Φυσικά αυτό προαπαιτεί αρκετό χρόνο και ποικίλες δραστηριότητες κατά τη διάρκεια της χρονιάς.
ΔΡΑΣΤΗΡΙΟΤΗΤΕΣ
1Η ΔΡΑΣΤΗΡΙΟΤΗΤΑ
ΤΙΤΛΟΣ ΔΡΑΣΤΗΡΙΟΤΗΤΑΣ: ΓΝΩΡΙΖΟΝΤΑΣ ΤΑ ΞΥΛΑΚΙΑ CUISENAIRE
ΜΑΘΗΣΙΑΚΟΙ ΣΤΟΧΟΙ: Στόχος αυτής της δραστηριότητας είναι να έρθουν τα παιδιά σε επαφή με τα ξυλάκια, να μάθουν τη χρήση τους και τη σχέση τους με τους αριθμούς.
ΑΦΟΡΜΗ- ΕΝΑΥΣΜΑ: Έναυσμα για αυτή τη δραστηριότητα αποτελούν οι ράβδοι Cuisenaire που έχουν τοποθετηθεί στην γωνιά των μαθηματικών απ’ τη νηπιαγωγό και κεντρίζουν το ενδιαφέρον των παιδιών κατά τις ελεύθερες δραστηριότητες.
ΠΕΡΙΓΡΑΦΗ: Παρουσιάζουμε στα παιδιά τις ράβδους σε χειραπτική μορφή. Τους δίνουμε χρόνο να τις επεξεργαστούν, να παίξουν, να πειραματιστούν. Αφού εξοικειωθούν με αυτές, τους ζητάμε να παρατηρήσουν και συζητάμε το διαφορετικό μέγεθος που έχει η κάθεμια και το αντίστοιχο χρώμα ανάλογα με το μέγεθός της (μήκος). Εξηγούμε στα παιδιά ότι η κάθε ράβδος αντιστοιχεί και σε έναν αριθμό. Τοποθετούμε καρτέλες με αριθμούς επάνω στο τραπέζι (κάθε κάρτα απεικονίζει ένα αριθμό). Ζητάμε από τα παιδιά να αντιστοιχίσουν τις ράβδους με τον αριθμό που απεικονίζουν. Χρησιμοποιούμε μία εικόνα που θα καθοδηγήσει τα παιδιά στην αντιστοίχηση.
ΕΠΟΠΤΙΚΑ ΜΕΣΑ: ράβδοι Cuisenaire, καρτέλες με αριθμούς.
ΜΕΘΟΔΟΙ: Παρατήρηση, καταιγισμός ιδεών, ομαδοσυνεργατική.
ΔΙΑΡΚΕΙΑ: 40-45 ΛΕΠΤΆ
ΑΞΙΟΛΟΓΗΣΗ: Δίνουμε στα παιδιά φύλλα εργασίας με δυο στήλες όπου στη μια θα είναι οι ράβδοι και στην άλλη οι αριθμοί και ζητάμε από τα παιδιά να κάνουν την αντιστοίχηση. Εδώ μπορούν να κατανοηθούν και τυχόν απορίες των παιδιών ή η δυσκολία στο να καταλάβουν τις ράβδους και τη χρήση τους.
Αντίστοιχη δραστηριότητα κάνουμε και στο kidspiration, , όπου τα παιδιά δείχνουν μεγαλύτερο ενδιαφέρον στη χρήση του υπολογιστή.
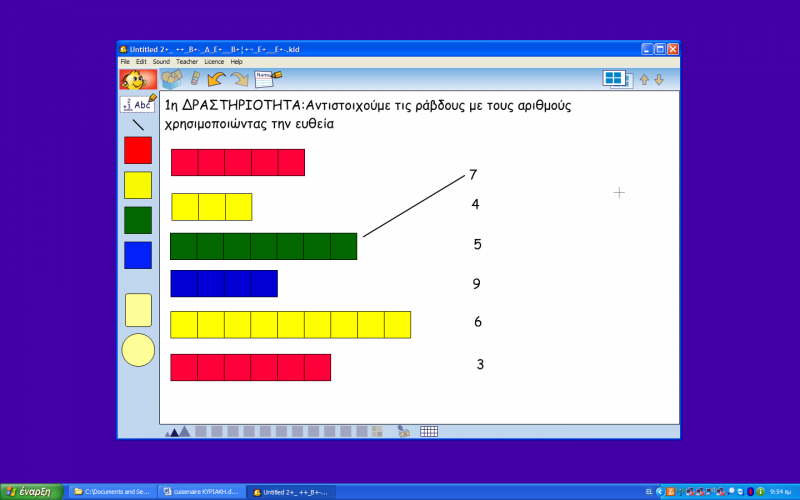
ΠΕΡΙΓΡΑΦΗ ΨΗΦΙΑΚΗΣ ΔΡΑΣΤΗΡΙΟΤΗΤΑΣ
Στη ψηφιακή δραστηριότητα στο kidspiration υπάρχουν δύο στήλες όπου στη μια υπάρχουν διαφόρων χρωμάτων και μηκών ράβδοι και στη άλλη υπάρχουν αριθμοί. Τα παιδιά καλούνται να μετρήσουν τις μονάδες των κάθε ράβδων και να τις ενώσουν με την ευθεία με τον αντίστοιχο αριθμό. Τα παιδιά εξοικειώνονται με τους αριθμούς και κατανοούν πως η μικρότερη ράβδος αντιστοιχεί σε μικρό αριθμό και όσο μεγαλώνουν οι ράβδοι ανεβαίνουν και οι αριθμοί. Σε σύγκριση με τα χειραπτικά υλικά το kidspiration βοηθάει περισσότερο τα παιδιά να κάνουν την αντιστοίχηση καθώς είναι πιο εύκολο να μετρούν τις μονάδες και να βρίσκουν τον αριθμό ενώ με τα ξυλάκια τους βοηθάει περισσότερο η σύγκριση των μεγεθών.
2Η ΔΡΑΣΤΗΡΙΟΤΗΤΑ
ΤΙΤΛΟΣ ΔΡΑΣΤΗΡΙΟΤΗΤΑΣ: ΟΙ ΡΑΒΔΟΙ CUISENAIRE ΚΑΙ Η ΣΧΕΣΗ ΤΟΥΣ ΜΕ ΤΟ ΜΗΚΟΣ
ΜΑΘΗΣΙΑΚΟΙ ΣΤΟΧΟΙ: Στόχος αυτής της δραστηριότητας είναι να μάθουν τα παιδιά ότι οι ράβδοι εκτός του ότι αντιστοιχούν σε έναν αριθμό αντιστοιχούν και σε ένα μήκος (π.χ το μικρότερο, το 1 αντιστοιχεί σε 1 cm, το 2 σε 2 cm κ. ο. κ )
ΑΦΟΡΜΗ ΕΝΑΥΣΜΑ: Αφορμή θα αποτελέσουν τα ξυλάκια Cuisenaire που έμαθαν και χρησιμοποίησαν τα παιδιά στη προηγούμενη δραστηριότητα αλλά και μια καρτέλα που απεικονίζει τους αριθμούς και δίπλα τις ράβδους.

ΠΕΡΙΓΡΑΦΗ: Δείχνουμε στα παιδιά τη καρτέλα με τους αριθμούς και τις ράβδους και συζητάμε παρατηρώντας την τη διαφορά στο μέγεθος των ράβδων. Έπειτα εξηγούμε στα παιδιά ότι η μικρότερη ράβδος, η άσπρη ισούται με 1 εκατοστό, η δεύτερη κόκκινη με 2 εκατοστά και συνεχίζουμε το ίδιο για όλες τις ράβδους. Μετά από τη συζήτηση και αφού έχουμε καταλάβει ότι τα παιδιά έχουν κατανοήσει τη σχέση των ράβδων με το μήκος τους ζητάμε να μας πουν αλλά και να μας δείξουν με τις ράβδους τη σχέση μεταξύ τους. Ξεκινάμε με τις μικρότερες π.χ η κόκκινη με πόσες άσπρες ισούται ή η πράσινη ανοιχτή με πόσες άσπρες και προχωράμε σε ποιο σύνθετα ερωτήματα αφού τα παιδιά έχουν κατανοήσει τα απλά όπως η πορτοκαλί ράβδος με πόσες άσπρες ισούται ή η πράσινες με πόσες κόκκινες. Η χρήση των ράβδων θα βοηθήσει πολύ τα παιδιά στις απαντήσεις τους. Την ίδια δραστηριότητα μπορούμε να κάνουμε και στο kidspiration και να λειτουργήσει και ως αξιολόγηση. Επίσης παρουσιάζουμε στα παιδιά τη σκάλα των ράβδων ώστε να κατανοήσουν τα παιδιά την έννοια της ισότητας του μήκους και να διαπιστώσουν πως μια ράβδος μπορεί να ισούται με δύο ή και παραπάνω ράβδους.

ΕΠΟΠΤΙΚΑ ΜΕΣΑ: Καρτέλα με τους αριθμούς και τις ράβδους, καρτέλα με τη σκάλα των ράβδων, ράβδοι Cuisenaire
ΔΙΑΡΚΕΙΑ: 40-45 λεπτά
ΜΕΘΟΔΟΙ: Παρατήρηση, Συζήτηση, Ανακάλυψη ή επίλυση προβλήματος, Ομαδοσυνεργατική
ΑΞΙΟΛΟΓΗΣΗ: Σαν αξιολόγηση ζητάμε από τα παιδιά να δημιουργήσουν μια δική τους ατομική μακέτα με πλαστελίνες που η νηπιαγωγός έχει κόψει σε αναλογία μεγέθους με τις ράβδους. Τα παιδιά θα κατασκευάσουν τη δική τους ‘σκάλα των ράβδων’ ώστε να καταλάβουμε αν επιτεύχθηκε ο μαθησιακός στόχος της δραστηριότητας.
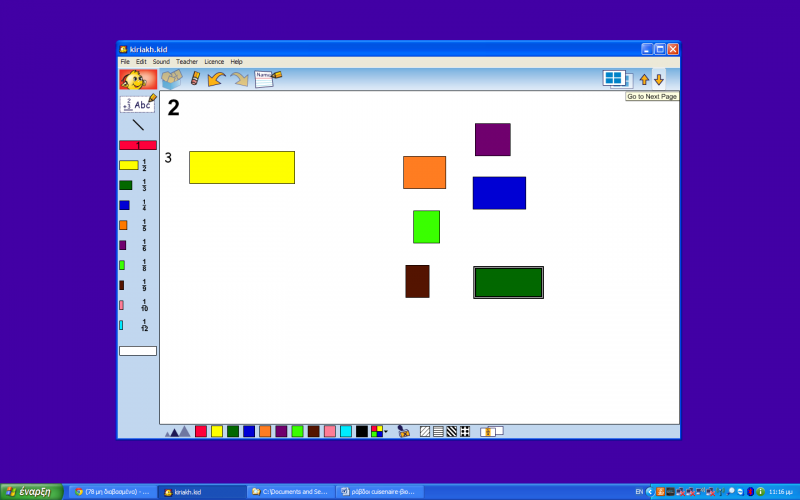
ΠΕΡΙΓΡΑΦΗ ΨΗΦΙΑΚΗΣ ΔΡΑΣΤΗΡΙΟΤΗΤΑΣ
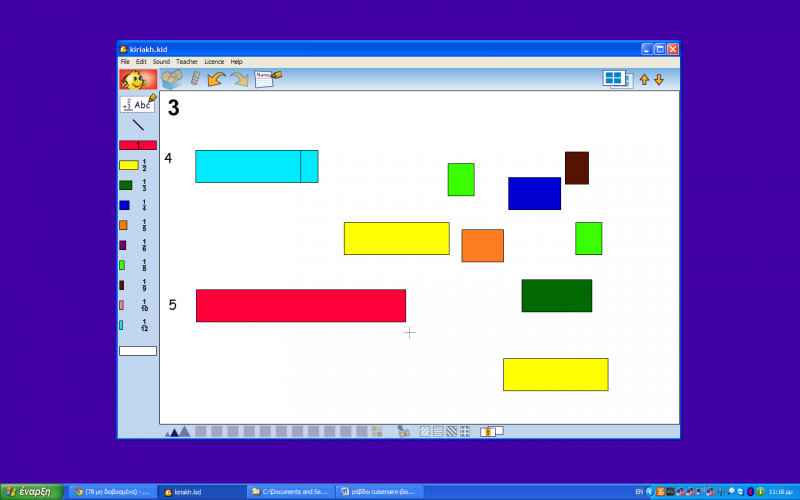
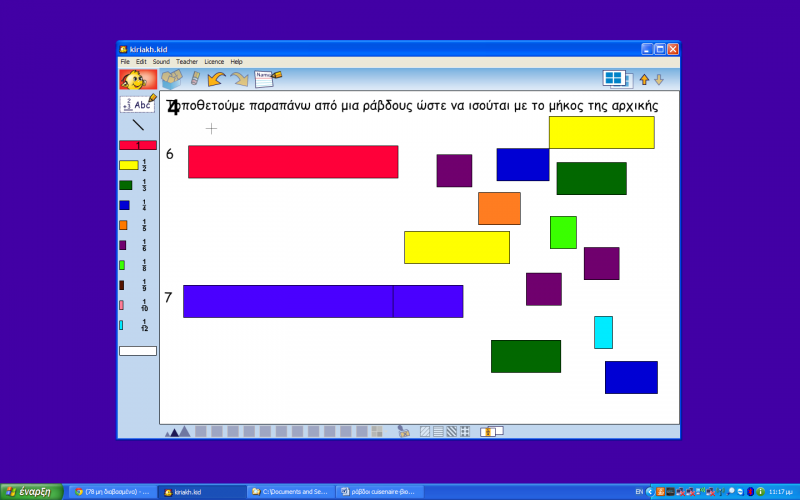
Στη ψηφιακή δραστηριότητα δίνονται στα παιδιά ράβδους και καλούνται να τοποθετήσουν από κάτω μικρότερες ράβδους ώστε το μήκος τους να ισούται με την αρχική ράβδο. Τα παιδιά θα πρέπει να δοκιμάσουν τα διάφορα μήκη που τους δίνονται ώστε να τοποθετήσουν τα ακριβή μεγέθη. Τα παιδιά θα βρουν πιο ενδιαφέρουσα τη ψηφιακή δραστηριότητα καθώς μπορούν να τη δουν και σαν παιχνίδι μέσα από την οποία όμως θα κατανοήσουν τη μαθησιακή έννοια.

3Η ΔΡΑΣΤΗΡΙΟΤΗΤΑ
ΤΙΤΛΟΣ ΔΡΑΣΤΗΡΙΟΤΗΤΑΣ: ΠΡΟΣΘΕΣΗ ΚΑΙ ΑΦΑΙΡΕΣΗ ΜΕ ΤΗ ΧΡΗΣΗ ΤΩΝ ΡΑΒΔΩΝ CUISENAIRE
ΜΑΘΗΣΙΑΚΟΙ ΣΤΟΧΟΙ: Στόχος αυτής της δραστηριότητας είναι να μάθουν τα παιδιά τη πράξη της πρόσθεσης και της αφαίρεσης μέσα από τα ξυλάκια Cuisenaire.
ΑΦΟΡΜΗ-ΕΝΑΥΣΜΑ: Αφορμή για αυτή τη δραστηριότητα αποτελεί η καρτέλα με τους ράβδους Cuisenaire αλλά και η σκάλα των ράβδων που βρίσκονται τοποθετημένα σε πίνακα μέσα στη τάξη. Επίσης και η ενασχόληση των παιδιών στις προηγούμενες δραστηριότητες με τις ράβδους.
ΠΕΡΙΓΡΑΦΗ: Μαζευόμαστε με τα παιδιά στη γωνιά της συζήτησης και μιλάμε για τις ράβδους αλλά και για τη πρόσθεση και την αφαίρεση και παρουσιάζουμε τα σύμβολά τους. (+, -). Χωρίζουμε τα παιδιά σε δύο ομάδες όπου η μία είναι η πρόσθεση και η άλλη είναι η αφαίρεση. Η ομάδα της πρόσθεσης θα προσθέτει αντικείμενα σε ένα τραπέζι ενώ η άλλη θα αφαιρεί. Αφού τα παιδιά έχουν κατανοήσει τις έννοιες της πρόσθεσης και της αφαίρεσης συνεχίζουμε τοποθετώντας πάνω στο τραπέζι τη πορτοκαλί ράβδο, η οποία είναι η μεγαλύτερη και ζητάμε από τα παιδιά να τοποθετήσουν τόσες ράβδους ώστε να καλύπτουν ακριβώς τη πορτοκαλί. Ταυτόχρονα ζητάμε από τα παιδιά να σημειώνουν από κάτω τον αριθμό τον οποίο χρησιμοποιούν βάζοντας ταυτόχρονα και το σύμβολο της πρόσθεσης. Σ’ αυτό θα τους βοηθήσει και η καρτέλα με τις ράβδους που δημιουργήθηκε σε προηγούμενη δραστηριότητα. Τα παιδιά εργάζονται ατομικά.
Π.χ. πορτοκαλί ράβδος και από κάτω δύο μωβ και θα χρειαστεί για να συμπληρωθεί το κενό μία κόκκινη.

Βοηθητικά θα μπορούσαν να συμπληρώσουν από κάτω, με λευκές ράβδους, που αντιστοιχούν στον αριθμό ένα, κάτι που θα διευκόλυνε τις πράξεις.
Από την ανωτέρω δραστηριότητα θα προκύψουν πολλοί συνδυασμοί.
Αντίστοιχη δραστηριότητα θα μπορούσε να είναι η αφαίρεση με την αντίστροφη διαδικασία.
Δίνουμε στα παιδιά την αρχική ράβδο, βάζουμε από κάτω μία μικρότερη. Το αποτέλεσμα της αφαίρεσης θα είναι η ράβδος που καλύπτει ακριβώς το κενό.
Αντίστοιχη δραστηριότητα μπορεί να γίνει και στο kidspiration.
ΕΠΟΠΤΙΚΑ ΜΕΣΑ: Ράβδοι Cuisenaire, μολύβι, χαρτί Α4, καρτέλα με
τις ράβδους.
ΔΙΑΡΚΕΙΑ: 40-45 λεπτά
ΜΕΘΟΔΟΙ: Ερωτήσεις- Απαντήσεις, Συζήτηση, Ομαδοσυνεργατική στη συζήτηση και στην εκμάθηση των συμβόλων, Εξατομίκευση στις πράξεις.
ΑΞΙΟΛΟΓΗΣΗ: Σαν αξιολόγηση θα χρησιμοποιήσουμε φύλλα εργασίας. Αυτά θα έχουν ράβδους και θα ζητάμε από τα παιδιά να συμπληρώσουν τους αριθμούς που αντιστοιχούν στις ράβδους αλλά και πιο τη ράβδο που λείπει και τον αριθμό.
ΠΕΡΙΓΡΑΦΗ ΨΗΦΙΑΚΗΣ ΔΡΑΣΤΗΡΙΟΤΗΤΑΣ
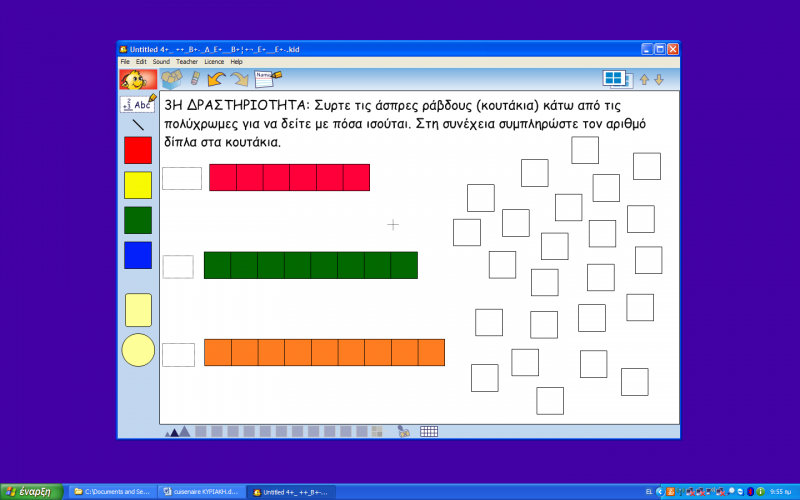
Στο kidspiration δίνουμε στα παιδιά μεγάλες ράβδους και ζητάμε από τα παιδιά να τοποθετήσουν από κάτω τις άσπρες ράβδους που ισούται με τη μονάδα. Ζητάμε από τα παιδιά να προσθέσουν τις ράβδους και να βρουν ποιος αριθμός προκύπτει. Στη συνέχεια με τη βοήθεια της νηπιαγωγού γράφουν μέσα στο κενό κουτάκι τον αριθμό που αντιστοιχεί. Χρησιμοποιούμε αρχικά τη μονάδα γιατί είναι πιο εύκολο για το αρχικό στάδιο της γνώσης της μαθησιακής έννοιας. Στη συνέχεια μπορούμε να χρησιμοποιήσουμε κ μεγαλύτερα μεγέθη.
ΓΕΝΙΚΗ ΑΞΙΟΛΟΓΗΣΗ
Σαν αξιολόγηση της όλης μάθησης των ράβδων Cuisenaire και της χρήσης τους θα χρησιμοποιηθεί ένα δέντρο κολλάζ με τα φύλλα του όπου τα παιδιά θα συμπληρώνουν καθημερινά ανάλογα με τις οδηγίες της νηπιαγωγού.


Το δεντράκι θα πρέπει να έχει πυκνά κλαδάκια και να πλαστικοποιηθεί για να μη χαλάσει . Αφού το πλαστικοποιήσουμε μπορούμε να βάλουμε χριτς - χρατς , για να μπορούν να σταθούν τα φύλλα . Η πολυχρωμία των φθινοπωρινών φύλλων έκανε πιο ελκυστική τη δραστηριότητα. Το δεντράκι το τοποθετούμε δίπλα στη καρτέλα με τις ράβδους Cuisenaire. Δημιουργούμε τα φύλλα κατά μέγεθος από το μικρότερο στο μεγαλύτερο και κάθε φορά ζητάμε από τα παιδιά να τοποθετήσουν ανάλογα με το μέγεθος. Όπως και οι ράβδοι από το μικρότερο στο μεγαλύτερο. Μπορούμε επίσης για παράδειγμα να ζητήσουμε από τα παιδιά να τοποθετήσουν τα φύλλα από τα μεγαλύτερα στη κορυφή και κατεβαίνοντας να μικραίνει και το μέγαθος.


Επίσης μπορούν να κάνουν και αριθμογραμμές, οι οποίες μοιάζουν με τη καρτέλα των ράβδων.
Τα παιδιά μπορούν επίσης να σχηματίσουν και τους αριθμούς με τα φύλλα.
Τα παιδία θα βρουν πολύ διασκεδαστική αυτή τη διαδικασία και θα κατανοήσουν τις μαθηματικές έννοιες που έχουν σχέση με τις ράβδους όπως το μικρότερο- μεγαλύτερο, η αρίθμηση αλλά και η πρόσθεση.


Σύγκριση χειραπτικών και ψηφιακών μικρόκοσμων
Χειραπτικός μικρόκοσμος
Χρησιμοποιώντας το χειραπτικό υλικό, δηλαδή τις ράβδους, ο μαθητής έχει τη δυνατότητα να πειραματιστεί, να δοκιμάσει και να επαληθεύσει όσα σκέφτεται.
Οι ράβδοι τον βοηθούν :
Α) να συγκρίνει ευκολότερα δύο μεγέθη, καθώς είναι άνισες μεταξύ τους,
Β) να διαχωρίσει δύο μεγέθη που έχουν μικρή διαφορά μεταξύ τους, καθώς έχουν διαφορετικά χρώματα ανά διαφορά εκατοστού, πχ. Το 2 με το 3 (κόκκινο και λαχανί αντίστοιχα)
Ο μαθητής έρχεται σε επαφή με πολλά μεγέθη και χρώματα. Αυτό επιτυγχάνει την εξοικείωση σε μαθηματικές έννοιες και πράξεις. Διατηρείται ζωντανό το ενδιαφέρον του και η περιέργεια του για τη συνέχεια της δραστηριότητας. Αποτελεί ενδιαφέρουσα διαδικασία, ειδικά για τους κιναισθητικού τύπου μαθητές.
Επιπλέον, οι δραστηριότητες με τις ράβδους, προσφέρουν τη δυνατότητα για συνεργατική μάθηση, δραστηριότητες σε ομάδες. Αυτό βοηθά στην κοινωνικοποίηση των παιδιών, στην βελτίωση της παρατηρητικότητάς τους, στη δημιουργία ανταγωνιστικού πνεύματος αλλά και συνύπαρξης και συνεργασίας με τους συμμαθητές τους.
Βέβαια αποτελεί χρήσιμο εργαλείο και για την ατομική πρόοδο του μαθητή, καθώς μπορεί να χρησιμοποιήσει οποιαδήποτε στιγμή της ημέρας τις ράβδους, προκειμένου να επαληθεύσει κάποιες σκέψεις ή πράξεις που έχει στο μυαλό του. Έχει τη δυνατότητα να αγγίξει τις ράβδους, να τις παρατηρήσει καλύτερα, να τις τοποθετήσει δίπλα-δίπλα, ώστε να είναι σίγουρος για τα αποτελέσματά του και να αποκλείσει πιθανότητες λάθους.
Ψηφιακός Μικρόκοσμος
Ο ψηφιακός μικρόκοσμος παρουσιάζει ακόμη μεγαλύτερο ενδιαφέρον. Τα παιδιά είναι αρκετά εξοικειωμένα με τον υπολογιστή και την τεχνολογία. Αντιμετωπίζουν τα ηλεκτρονικά φύλλα εργασίας ως παιχνίδι και αποζητούν όλο και περισσότερη ώρα, για την ενασχόληση τους με αυτά. Παρέχει λοιπόν κίνητρα στους μαθητές και στην συγκεκριμένη περίπτωση αποτελεί ένα παιχνίδι χρωμάτων και αριθμών, οπότε και μια ευχάριστη διαδικασία αλλά και μια ενδιαφέρουσα εξάσκηση της νεοαποκτηθείσας γνώσης.
Μέσω των ψηφιακών μικρόκοσμων, ο μαθητής κατανοεί σε βάθος τις γνώσεις και να τις αφομοιώνει. Οι μαθητές αλλά και οι εκπαιδευτικοί μπορούν να μοιραστούν ιδέες και σκέψεις, χρησιμοποιώντας εικόνες και κείμενο, κάνοντας έτσι πιο δημιουργική τη διδασκαλία. Η κατανόηση των μαθηματικών εννοιών, γίνεται μέσα από εικόνες και σχήματα . Τα μοντέλα που δημιουργούνται στο περιβάλλον του υπολογιστή συμβάλλουν στην διαδραστική μάθηση και στην ενεργή συμμετοχή του παιδιού.
Στον Η/Υ ο μαθητής δουλεύει ατομικά. Ο ψηφιακός μικρόκοσμος φαίνεται να προάγει την ανακαλυπτική μάθηση, καθώς βρίσκει μόνος του νέους συνδυασμούς. Ακόμη συμβάλλει στην αύξηση της ενεργητικής και αυτόνομης συμπεριφοράς των μαθητών. Το παιδί παίρνει πρωτοβουλίες, δίχως να φοβάται για περίπτωση λάθους, αφού έχει τη δυνατότητα αμέσως μετά να το διορθώσει και να ξεκινήσει από την αρχή την προσπάθειά του.
Είναι σημαντικό να αναφέρουμε ότι η διδασκαλία μέσω του υπολογιστή, υποστηρίζει τους διαφορετικούς ρυθμούς μάθησης και αντιμετωπίζει τις ιδιαιτερότητες των μαθητών. Το παιδί μπορεί να εργαστεί με το δικό του ρυθμό, οπότε αντιλαμβανόμαστε ότι πρόκειται για μια διαδικασία ευπροσάρμοστη στις ανάγκες του.
Η επικοινωνία μαθητή-εκπαιδευτικού σε αυτή τη διαδικασία παίζει καθοριστικό ρόλο. Ο εκπαιδευτικός θα πρέπει να καθοδηγήσει το μαθητή στην νέα αυτή μέθοδο διδασκαλίας, προκειμένου να του προκαλέσει την περιέργεια και το ενδιαφέρον. Έτσι ο μαθητής να ακολουθήσει τα βήματα του εκπαιδευτικού με ευχαρίστηση και δίψα για νέα μάθηση.