Τέσσερις διδασκαλίες για τα δεκαδικά κλάσματα
Submitted by ltme on Wed, 04/22/2015 - 10:03
Το υλικό διδασκαλίας που παρουσιάζεται σε αυτή την εργασία αφορά τέσσερις διδασκαλίες για τα δεκαδικά κλάσματα για την Ε΄ τάξη του δημοτικού σχολείου. Έρευνες αναφέρουν ότι η διδασκαλία των κλασμάτων είναι ένα αντικείμενο ιδιαίτερα δύσκολο για τα παιδιά (Baroody, 1989, Reys, Suydam & Lindguist, 1989) και ότι πολλές φορές, ενώ οι μαθητές φαίνεται να παρουσιάζουν πλήρη κατανόηση των εννοιών που σχετίζονται με τα κλάσματα, στην πραγματικότητα κάτι τέτοιο μπορεί να απέχει πολύ από την πραγματικότητα. Οι μαθητές μπορεί να χρησιμοποιούν σωστά τους μαθηματικούς όρους, να λύνουν κάποια προβλήματα αλλά να αγνοούν πολλές σημαντικές πτυχές των σχετιζόμενων εννοιών. Η εικόνα που παρουσιάζουν μπορεί να είναι ιδιαιτέρως παραπλανητική. (Nunes & Bryant, 1996). Από την άλλη, αποτελέσματα ερευνών δείχνουν ότι και οι ίδιοι οι εκπαιδευτικοί αντιμετωπίζουν μεγαλύτερη δυσκολία στο να διδάξουν κλάσματα και αναλογίες από ότι να διδάξουν τους ακέραιους αριθμούς. (Anderson & Wong, 2007). Το υλικό που παρουσιάζεται στα πλαίσια αυτής της εργασίας χρησιμοποιεί στοιχεία γεωμετρίας και ζωγραφικής για να εισάγει τα παιδιά με ένα ευχάριστο τρόπο στη διδασκαλία των δεκαδικών κλασμάτων.
Στοχεύει να βοηθήσει τους μαθητές να οδηγηθούν σε μια πρώτη κατανόηση των εννοιών που εμπλέκονται. Ακόμα λαμβάνοντας υπόψη τα πιο κοινά λάθη που κάνουν οι μαθητές και τις δυσκολίες που συνήθως αντιμετωπίζουν, στοχεύει στο να δώσει την ευκαιρία για μια πρώτη διερεύνησή τους. Είναι προφανές ότι ένα τόσο ευρύ θέμα όπως η εκμάθηση των κλασμάτων δεν είναι δυνατό να καλυφθεί μέσα σε τέσσερις διδακτικές ώρες. Επίσης είναι προφανές ότι καθώς το κάθε τμήμα μαθητών έχει διαφορετικές ανάγκες και ικανότητες, οι χρόνοι διεξαγωγής του κάθε μαθήματος μπορεί να ποικίλουν. Για αυτό το λόγο δίνονται πιθανές επεκτάσεις των δραστηριοτήτων τις οποίες θα μπορούσε ο κάθε εκπαιδευτικός να χρησιμοποιήσει ανάλογα με την κρίση του. Τέλος, το σύνολο της εργασίας έχει αναρτηθεί στη ιστοσελίδα του συλλόγου αποφοίτων του Παιδαγωγικού Τμήματος Εκπαίδευσης του Α.Π.Θ. www.koundouras.blogspot.com προς χρήση όλων των ενδιαφερόμενων εκπαιδευτικών.
Τι προβλέπεται από το αναλυτικό πρόγραμμα: Στην ενότητα αυτή, και στον πρώτο πίνακα, παρουσιάζονται όσα προβλέπονται από τα νέα Αναλυτικά Προγράμματα που δημοσιεύτηκαν στο ΦΕΚ τεύχος β’ Αρ. φύλλου 303, στις 13 Μαρτίου 2003, σε σχέση με τους άξονες, γενικούς στόχους και θεμελιώδεις έννοιες διαθεματικής προσέγγισης για τα μαθήματα των Μαθηματικών (κλάσματα, δεκαδικά κλάσματα, γεωμετρία) και των Εικαστικών, από την Α’ δημοτικού έως και την Στ’ και τα οποία σχετίζονται με το υλικό που προτείνεται για τις τέσσερις διδασκαλίες. Επίσης, σε πίνακες που ακολουθούν παρουσιάζονται οι ειδικοί σκοποί ανά τάξη σε σχέση με τα κλάσματα και τα δεκαδικά κλάσματα.
Κλάσματα: Άξονες, γενικοί στόχοι, θεμελιώδεις έννοιες διαθεματικής προσέγγισης (σελ. 3984-5)
|
Γ |
Να γνωρίσουν τα κλάσματα και τους δεκαδικούς αριθμούς στους δεκαδικούς αριθμούς. |
|
Δ |
Να εξασκηθούν στις πράξεις με δεκαδικούς αριθμούς και δεκαδικά κλάσματα. |
|
Ε |
Να απαγγέλλουν, να διαβάζουν, να γράφουν και να διατάσουν φυσικούς μέχρι το 1.000.000.000 καθώς επίσης κλασματικούς και δεκαδικούς αριθμούς. Να εκτελούν πράξεις της πρόσθεσης, της αφαίρεσης, του πολλαπλασιασμού και της διαίρεσης φυσικών, κλασματικών και δεκαδικών αριθμών. |
|
ΣΤ |
Να απαγγέλλουν, να διαβάζουν, να γράφουν και να διατάσσουν φυσικούς, κλασματικούς και δεκαδικούς αριθμούς καθώς και να εκτελούν όλες τις πράξεις τους. |
KΛΑΣΜΑΤΑ (και δεκαδικά κλάσματα). Ειδικοί σκοποί (ανά τάξη)
Τάξη Γ (σελ. 3995). Στην τρίτη τάξη γίνεται η πρώτη γνωριμία των παιδιών με τα κλάσματα.
|
ΣΤΟΧΟΙ |
ΘΕΜΑΤΙΚΕΣ ΕΝΟΤΗΤΕΣ (διατιθέμενος χρόνος) |
|
Να γνωρίσουν τις κλασματατικές μονάδες (πχ. ½, ¼, 1/3, 1/8, 1/16, 1/5, 1/10 κλπ.) Να μπορούν να συγκρίνουν με τη βοήθεια κατάλληλων αναπαραστάσεων απλές κλασματικές μονάδες |
Αριθμοί και πράξεις Εισαγωγή στα «απλά» κλάσματα 10 ώρες |
Tάξη Δ (σελ. 3999)
Στην τετάρτη τάξη γίνεται κυρίως επεξεργασία των δεκαδικών αριθμών. Από τους πέντε συνολικά στόχους που εμφανίζονται οι δύο μόνο αφορούν δεκαδικά κλάσματα. Επίσης, εκτός από την ενότητα που παρουσιάζεται εδώ αφιερώνονται άλλες 7 διδακτικές ώρες αμιγώς στους δεκαδικούς αριθμούς.
|
ΣΤΟΧΟΙ |
ΘΕΜΑΤΙΚΕΣ ΕΝΟΤΗΤΕΣ (διατιθέμενος χρόνος) |
|
Οι μαθητές πρέπει να μπορούν: Να περνούν από ένα δεκαδικό αριθμό σε μια κλασματική δεκαδική γραφή και αντίστροφα. Να τοποθετούν με προσέγγιση δεκαδικά κλάσματα και δεκαδικούς αριθμούς στην αριθμογραμμή. |
Αριθμοί και πράξεις Δεκαδικά κλάσματα και δεκαδικοί αριθμοί 14 ώρες |
Τάξη Ε (σελ. 4002)
Στην Ε’ τάξη αφιερώνονται 5 ώρες για τη γραφή, ονομασία και διάταξη δεκαδικών αριθμών αλλά καμία αναφορά δε γίνεται στο αναλυτικό πρόγραμμα για τα δεκαδικά κλάσματα, ενώ αφιερώνονται συνολικά 12 ώρες για τα κλάσματα.
|
ΣΤΟΧΟΙ |
ΘΕΜΑΤΙΚΕΣ ΕΝΟΤΗΤΕΣ (διατιθέμενος χρόνος) |
|
Οι μαθητές πρέπει να μπορούν: Να δημιουργούν και να διακρίνουν ομώνυμα και ετερώνυμα κλάσματα. Να μετατρέπουν ετερώνυμα κλάσματα σε ομώνυμα. Να απλοποιούν κλάσματα Να συγκρίνουν και να διατάσσουν κλάσματα. Να μετατρέπουν κλάσματα σε μεικτούς αριθμούς. |
Αριθμοί και πράξεις Κλάσματα 6 ώρες |
|
Οι μαθητές πρέπει να μπορούν: Να προσθέτουν και να αφαιρούν κλάσματα. Να πολλαπλασιάζουν και να διαιρούν κλάσματα. Να επιλύουν απλά προβλήματα κλασμάτων. Να χρησιμοποιούν τη μέθοδο αναγωγής στην κλασματική μονάδα. |
Αριθμοί και πράξεις Πράξεις με κλάσματα 6 ώρες |
ΤΑΞΗ ΣΤ (σελ. 4006-7)
|
ΣΤΟΧΟΙ |
ΘΕΜΑΤΙΚΕΣ ΕΝΟΤΗΤΕΣ (διατιθέμενος χρόνος) |
|
Οι μαθητές πρέπει να μπορούν: Να διακρίνουν και να δημιουργούν ισοδύναμα κλάσματα. Να δημιουργούν και να διακρίνουν ομώνυμα και ετερώνυμα κλάσματα. Να συγκρίνουν και να διατάσσουν κλάσματα. Να μετατρέπουν κλάσματα σε μεικτούς αριθμούς. Να απλοποιούν κλάσματα. Να μετατρέπουν κλάσματα σε δεκαδικούς και αντίστροφα. Να χειρίζονται απλές παραστάσεις που συνδυάζουν κλάσματα και δεκαδικούς. |
Αριθμοί και πράξεις Κλάσματα 8 ώρες |
ΓΕΩΜΕΤΡΙΑ: Άξονες, γενικοί στόχοι, θεμελιώδεις έννοιες διαθεματικής προσέγγισης (σελ. 3984-5)
|
Β |
Να εξασκούνται στη σχεδίαση, αναπαραγωγή σχημάτων. Να καθορίζουν σημεία και να σχεδιάζουν ευθύγραμμα τμήματα και ευθείες |
|
Γ |
Να εξασκούνται στην περιγραφή, αναπαραγωγή και σχεδιασμό γεωμετρικών σχημάτων… καθώς και στην εφαρμογή τεχνικών σχεδίασης κάθετων ευθειών με τη βοήθεια γεωμετρικών οργάνων |
|
Δ |
Να εξασκούνται με τη βοήθεια οργάνων στη χάραξη παράλληλων και κάθετων ευθειών |
|
Ε |
Να χαράζουν γεωμετρικά σχήματα με τη βοήθεια οργάνων |
|
ΣΤ |
Να εξασκούνται στο σχεδιασμό ευθύγραμμων τμημάτων |
ΕΙΚΑΣΤΙΚΑ: Άξονες, γενικοί στόχοι, θεμελιώδεις έννοιες διαθεματικής προσέγγισης(σελ. 3827-8)
|
Α-Β |
Να χρησιμοποιεί την τέχνη, για να συμπληρώνει άλλα μαθήματα |
|
Γ-Δ |
Να χρησιμοποιεί τις εικαστικές τέχνες διαθεματικά με τα άλλα μαθήματα |
|
Ε-Στ |
Να χρησιμοποιεί τις γνώσεις του για τις εικαστικές τέχνες στα άλλα μαθήματα |
Τι υλοποιείται στα βιβλία του μαθητή: Από τους παραπάνω πίνακες είναι προφανές ότι η πρώτη γνωριμία των παιδιών με τα κλάσματα προβλέπεται να γίνει κατά την φοίτησή τους στην Γ’ δημοτικού. Έτσι από τον πίνακα περιεχομένων του βιβλίου του δασκάλου της αντίστοιχης τάξης βλέπουμε τις ενότητες που πραγματεύονται σχετικά θέματα.
|
Δεύτερη περίοδος 4η ενότητα |
|
22ο μάθημα Εισαγωγή στα κλάσματα |
|
23ο μάθημα Οι κλασματικές μονάδες |
|
24ο μάθημα Οι κλασματικές μονάδες και οι απλοί κλασματικοί αριθμοί |
|
25ο μάθημα Ισοδύναμα κλάσματα |
|
26ο μάθημα Επαναληπτικό |
|
6η ενότητα |
|
34ο μάθημα Δεκαδικά κλάσματα |
|
35ο μάθημα Δεκαδικά κλάσματα και δεκαδικοί αριθμοί |
|
Τρίτη περίοδος 9η ενότητα |
|
57ο μάθημα Κλάσματα και δεκαδικοί |
Ας δούμε όμως τους στόχους του 34ου μαθήματος (το οποίο είναι αυτό που πραγματεύεται αποκλειστικά τα δεκαδικά κλάσματα) όπως παρουσιάζονται στο βιβλίο του δασκάλου (σελ. 99).
Στόχοι: Στο κεφάλαιο αυτό θα μελετήσουμε περισσότερο σε βάθος τα δεκαδικά κλάσματα, δηλαδή, τα κλάσματα στα οποία ο παρονομαστής είναι δύναμη του δέκα. Θα οδηγήσουμε λοιπόν τους μαθητές να:Κατανοούν, διαβάζουν και να γράφουν τα δεκαδικά κλάσματα, δηλαδή, τα δέκατα, τα εκατοστά και τα χιλιοστά. Βρίσκουν, και να γράφουν ένα δεκαδικό κλάσμα ως άθροισμα άλλων δεκαδικών κλασμάτων, π.χ. 23/100 = 20/100 + 3/100 = 2/10 + 3/10. Βρίσκουν, και να γράφουν ένα δεκαδικό κλάσμα ως άθροισμα ενός ακεραίου και ενός δεκαδικού κλάσματος μικρότερου της μονάδας π.χ. 23/10 = 2 + 3/10. Περιορίζουν ένα δεκαδικό κλάσμα από δύο διαδοχικούς φυσικούς αριθμούς , π.χ. 2 < 23/10 < 3.
Θα περιοριστούμε εδώ στο να σχολιάσουμε τα εξής σε σχέση με την πολλαπλότητα των στόχων και τις πιθανότητες επίτευξής τους από τον εκπαιδευτικό σε μία διδακτική ώρα. Γνωρίζουμε από τη γνωστική ψυχολογία ότι, όταν προσφέρονται πολλές πληροφορίες στους μαθητές και μάλιστα πολύ γρήγορα, οι μαθητές δεν έχουν την ικανότητα να τις συγκρατήσουν όλες και ότι αντίθετα πρέπει να εστιάσουμε και να διατηρήσουμε την προσοχή τους σε συγκεκριμένες πληροφορίες κάθε φορά (Κολιάδης, 2002). Θα πρέπει ακόμα να παρατηρήσει κανείς ότι οι στόχοι δεν είναι μόνο τέσσερις όπως εμφανίζονται, αλλά ότι ο κάθε ένας από τους στόχους αναλύεται ουσιαστικά σε υπο-στόχους κάτι που δυσχεραίνει εκπαιδευτικούς και μαθητές ακόμη περισσότερο. Στην Δ’ Δημοτικού βλέπουμε από τον πίνακα περιεχομένων του βιβλίου του μαθητή ότι δεν υπάρχει κανένα κεφάλαιο το οποίο να πραγματεύεται κλάσματα. Δεκαδικά κλάσματα και κοινά κλάσματα εμφανίζονται στα κεφάλαια 15-19, 22, 24, 31 και 50 ως μία ακόμα μορφή συμβολισμού. Τα κεφάλαια αυτά πραγματεύονται κυρίως δεκαδικούς αριθμούς, εμβαδόν, ώρα και βάρος, Το γεγονός ότι τα παραπάνω κεφάλαια πραγματεύονται κυρίως άλλα θέματα και το ότι κάποια κλάσματα εμφανίζονται μόνο στο συμπέρασμα, σημαίνει ότι ουσιαστικά δεν γίνεται συστηματική προσπάθεια διδασκαλίας των κλασμάτων στην Δ’ Τάξη.
Το κεφάλαιο στο οποίο γίνεται άμεσα η αναφορά στους διαφορετικούς τρόπους συμβολισμού είναι το 24ο στο συμπέρασμα του οποίου αναφέρεται: Όταν διαιρούμε έναν αριθμό με το 10, 100, 1.000, η υποδιαστολή μετακινείται αριστερά, τόσες θέσεις όσα μηδενικά έχει ο διαιρέτης. /Κάθε δεκαδικός αριθμός μπορεί να γραφεί ως δεκαδικό κλάσμα και αντιστρόφως. Π.χ. 0,3=3/10, 7,04=704/100 και 12/100=0,12. / Κάθε δεκαδικός αριθμός και κάθε δεκαδικό κλάσμα μπορεί να γραφτεί ως το αποτέλεσμα μιας διαίρεσης που έχει ως διαιρέτη το 10, το 100, το 1.000… Π.χ. 2,65=265/100=265:100. Όπως θα δούμε και παρακάτω στο τμήμα της εργασίας που αναπτύσσεται η σχετική με τα κλάσματα θεωρία, η εισαγωγή των παιδιών στο συμβολισμό χωρίς να έχει προηγηθεί κατανόηση της έννοιας αποτελεί μία από τις αιτίες των δυσκολιών που τα παιδιά αντιμετωπίζουν με τα κλάσματα (Reys et al, 1989). Είναι γνωστό ότι όταν οι ενήλικες προσπαθούν να επιβάλλουν μαθηματικές έννοιες στα παιδiά πρόωρα η μάθηση είναι καθαρά λεκτική. (Hughes, 1996). Ως συνέπεια των παραπάνω οι μαθητές τελικά εισάγονται στην Ε’ Δημοτικού χωρίς να έχουν σαφή κατανόηση της έννοιας των κλασμάτων.
Τα κεφάλαια 7 –13 του βιβλίου του μαθητή της Ε’ τάξης πραγματεύονται δεκαδικούς αριθμούς και δεκαδικά κλάσματα μέσα από προβλήματα με ένα τρόπο που υποδηλώνει ότι τα παιδιά κατέχουν ήδη τις έννοιες. Στο βιβλίο του δασκάλου (κεφ. 7, σελ 61) η έννοια του κλάσματος θεωρείται ως προαπαιτούμενη γνώση. Οι έννοιες που συνδέονται με τα κλάσματα ουσιαστικά δεν διδάσκονται στους μαθητές και οι τελευταίοι καλούνται να τις χρησιμοποιούν για να λύσουν ακριβώς τα προβλήματα που τίθενται από το βιβλίο. Παράλληλα στο ατομικό φύλλο 2ης αξιολόγησης που εμφανίζεται στο βιβλίο του δασκάλου, οι 6 γνωστικοί στόχοι από τους 11 που παρουσιάζονται και τους οποίους θα πρέπει να έχουν κατακτήσει οι μαθητές αφορούν ακριβώς τα δεκαδικά κλάσματα και είναι οι εξής:
|
(Να μπορεί να ) Μετατρέπει (ο μαθητής) δεκαδικό κλάσμα σε δεκαδικό αριθμό και αντίστροφα (γραφή, ανάγνωση, αθροιστική ανάλυση) |
|
Εξηγεί την ισοδυναμία δεκαδικών αριθμών που στο τέλος των δεκαδικών τους ψηφίων έχουν διαφορετικό αριθμό μηδενικών χρησιμοποιώντας τα δεκαδικά κλάσματα. |
|
Συγκρίνει, διατάσσει και παρεμβάλλει δεκαδικούς αριθμούς ή δεκαδικά κλάσματα και δείχνουν στην αριθμογραμμή. |
|
Κάνει νοερούς υπολογισμούς με δεκαδικούς αριθμούς και δεκαδικά κλάσματα. |
|
Στρογγυλοποιεί δεκαδικούς αριθμούς και δεκαδικά κλάσματα αναγνωρίζοντας το σφάλμα της εκτίμησης κάθε φορά. |
|
Αναγνωρίζει τη μονάδα αναφοράς στο αποτέλεσμα μετρήσεων που εκφράζεται με δεκαδικό αριθμό ή δεκαδικό κλάσμα. |
Κατά συνέπεια θεωρούμε πρώτον ότι η γνώση των δεκαδικών κλασμάτων θεωρείται απαραίτητο να κατακτηθεί από τους μαθητές και δεύτερον ότι παρουσιάζεται ένα ουσιαστικό κενό στη διδασκαλία των κοινών κλασμάτων γενικότερα αλλά και των δεκαδικών κλασμάτων ειδικότερα στη συγκεκριμένη τάξη. Για το λόγο αυτό εντάσσουμε τις τέσσερις διδασκαλίες για τα δεκαδικά κλάσματα στην αρχή της ύλης της Ε’ Δημοτικού, ακριβώς πριν από το 7ο μάθημα. Πρέπει βέβαια να σημειώσουμε πώς το γεγονός ότι έχουμε εντάξει το υλικό στο σημείο αυτό δεν είναι δεσμευτικό. Καθώς οι ασκήσεις που παρουσιάζονται στο υλικό είναι διαβαθμισμένης δυσκολίας επιτρέπουν τη χρήση τους και σε άλλες τάξεις ανάλογα με τις ανάγκες, τις δυνατότητες της τάξης και τους στόχους του εκπαιδευτικού. Έτσι αν ο εκπαιδευτικός θεωρεί σκόπιμο ότι θα πρέπει για κάποιους λόγους να εισάγει τους μαθητές σε ορισμένες από τις έννοιες που πραγματεύεται το υλικό κάποια άλλη στιγμή, μπορεί κάλλιστα να επιλέξει τις δραστηριότητες που θεωρεί ότι τον εξυπηρετούν.
Η διδασκαλία των κλασμάτων στο δημοτικό σχολείο: Παρότι η εκμάθηση των κλασμάτων είναι μια περιοχή των μαθηματικών που τα παιδιά βρίσκουν ιδιαίτερα προκλητική (Anderson & Wong, 2007). τα κλάσματα, όπως έχει ήδη αναφερθεί στην εισαγωγή, θεωρούνται δύσκολο αντικείμενο και πραγματικά πολλά παιδιά αντιμετωπίζουν σημαντικές δυσκολίες με την κατανόησή τους. (Baroody, 1989, Reys, Suydam & Lindguist, 1989). Τα αποτελέσματα πολλών ερευνών, ειδικά σε σχέση με την κατανόηση των δεκαδικών κλασμάτων, που περιλαμβάνουν τόσο μαθητές του δημοτικού όσο και ενήλικες παρέχουν σημαντικές ενδείξεις ότι το σύστημα των δεκαδικών κλασμάτων δεν είναι ούτε ιδιαίτερα απλό, ούτε γενικά κατανοητό. (Irwin, 2001) Οι δυσκολίες που μπορεί να αντιμετωπίζουν τα παιδιά μπορεί να οφείλονται στο γεγονός ότι πολλές φορές η διδασκαλία προχωρά απευθείας στο συμβολισμό και στην εκμάθηση κανόνων και διαδικασιών χωρίς να έχει προηγηθεί ουσιαστική κατανόηση των αριθμών και των λειτουργιών τους. (Reys et al, 1989) Στο σχολείο τα παιδιά εισάγονται πολλές φορές απευθείας στους συμβολισμούς των κλασμάτων χωρίς να έχει προηγηθεί ουσιαστική κατανόηση (Baroody, 1989). Όταν η εκπαίδευση επικεντρώνεται σε αφηρημένα σύμβολα και απομνημόνευση όρων, ορισμών και διαδικασιών, τα αποτελέσματα όσον αφορά την κατανόηση και τη δυνατότητα εφαρμογής της γνώσης στην καθημερινή ζωή είναι μάλλον φτωχά. (Baroody, 1989) Στην πραγματικότητα έχει παρατηρηθεί πολλές φορές ένα ιδιαίτερα ανησυχητικό χάσμα ανάμεσα στο πώς χρησιμοποιούν τα παιδιά τα μαθηματικά σύμβολα στην τάξη και στην ικανότητά τους να τα εφαρμόζουν σε προβλήματα που συναντούν αλλού. (Hughes, 1996).
Γενικές διδακτικές αρχές: Σήμερα η πιο βασική ιδέα στη διδακτική των μαθηματικών είναι ότι τα μαθηματικά έχουν νόημα (Van de Walle, 2005). Όλες οι αρχές και οι μέθοδοι που αποκαλούνται «προοδευτικές» θεωρούν πάντα ως πιο σημαντική την κατανόηση. Μάλιστα, όταν το έργο που δίνεται στα παιδιά έχει από τη φύση του νόημα, τότε τα παιδιά διευκολύνονται στο να δείξουν τις ικανότητές τους. (Hughes, 1996). Η εκπαίδευση κατά συνέπεια θα πρέπει πρώτα να επικεντρώνεται και να χτίζει πάνω στη διαισθητική γνώση και στην ανεπίσημη γνώση των παιδιών. (Baroody, 1989) Μια δεύτερη βασική παραδοχή αφορά το γεγονός ότι η εκπαίδευση θα πρέπει να ξεκινά και να χτίζει πάνω σε συγκεκριμένες εμπειρίες (Baroody, 1989). Είναι γνωστό ότι η γνωστική ανάπτυξη του ατόμου ακολουθεί μια σειρά από επάλληλα εξελικτικά στάδια. Κάθε επόμενο στάδιο αποτελεί ένα πολυπλοκότερο τρόπο εσωτερικής αναπαράστασης της εξωτερικής πραγματικότητας. Τα τρία αυτά στάδια συνυπάρχουν στο παιδί ανεξάρτητα από την ηλικία, αλλά χρησιμοποιούνται σε διαφορετικό βαθμό σε κάθε στάδιο:
α) πραξιακή αναπαράσταση: αποτελεί ένα τρόπο μάθησης με δράση, πράξη, μίμηση και χειραγώγηση αντικειμένων. Πρέπει να προωθείται με τη μορφή της παραδειγματικής διδασκαλίας, δηλαδή ο εκπαιδευτικός και οι μαθητές κατά τη διδασκαλία χρησιμοποιούν αντικείμενα, πρότυπα επίδειξης και παραδείγματα. Πρόκειται για μάθηση που βασίζεται περισσότερο στην αρχή της δοκιμής και πλάνης παρά στη σκέψη.
β) εικονιστική αναπαράσταση: το άτομο σχηματίζει στο μυαλό του μια απεικόνιση του αντικειμένου, η αναπαράσταση του εξωτερικού κόσμου γίνεται με εσωτερικές πνευματικές εικόνες. Στη διδασκαλία χρησιμοποιούνται κατ’ επέκταση εικόνες, σχεδιαγράμματα, ζωγραφιές, σκίτσα αντικειμένων.
γ) συμβολική αναπαράσταση: στηρίζεται στην ανθρώπινη ικανότητα να αναπαριστά την εξωτερική πραγματικότητα με σύμβολα ή συστήματα συμβόλων αφηρημένα. Ο τρόπος αυτός αναπαράστασης αντιστοιχεί σε μεγάλο βαθμό με τη μάθηση διαμέσου του γραπτού και προφορικού λόγου. Η νοητική δραστηριότητα του παιδιού φαίνεται να βασίζεται στην ικανότητά του να χειρίζεται θεωρητικές έννοιες παρά στο να περιορίζεται στην εμπειρία. (Κολιάδης, 1997)
Τέλος, σημαντικό είναι να λαμβάνει υπόψη κανείς ότι η μάθηση και η ανάπτυξη μπορεί να εμφανίζονται ως ατομικό επίτευγμα αλλά οικοδομούνται μέσα σε συλλογικά πλαίσια. (Τριλιανός, 2000). Ο Vygotsky τόνισε τη σημασία της κοινωνικής αλληλεπίδρασης και υποστήριξε ότι το άτομο μέσα από την επικοινωνία του με το περιβάλλον οικειοποιείται το κοινωνικά παραχθέν γνωστικό προϊόν. Η διαμαθητική επικοινωνία και συνεργασία παίζει σημαντικό ρόλο στη μάθηση (Ματσαγγούρας, 2000). Στη σημασία της κοινωνικής αλληλεπίδρασης γίνεται αναφορά τόσο στο Αναλυτικό πρόγραμμα όσο και στα εισαγωγικά κείμενα των βιβλίων του δασκάλου.
Λαμβάνοντας κανείς υπόψη τις παραπάνω παραδοχές όταν σχεδιάζει κανείς ένα πρόγραμμα διδασκαλιών, θα πρέπει να προσπαθήσει να τις ενσωματώσει στις δραστηριότητες που απευθύνει στους μαθητές. Τα δεκαδικά κλάσματα συνήθως διδάσκονται στα σχολεία αλλά χρειάζεται να συνδεθούν με κάποιο τρόπο με τις υπάρχουσες γνώσεις των μαθητών. (Irwin, 2001) Τα περισσότερα παιδιά στο δημοτικό μπορούν να μάθουν για τα κλάσματα με ένα τρόπο που να έχει νόημα αν το αντικείμενο παρουσιαστεί με το σωστό τρόπο (Baroody, 1989). Δραστηριότητες που είναι ομαδικές ή/και δραστηριότητες που έχουν να κάνουν με δίκαιη μοιρασιά είναι απαραίτητες για να εισαχθούν τα παιδιά στο αντικείμενο και μπορούν να γίνουν τόσο με συνεχείς όσο και με ασυνεχείς ποσότητες (Baroody, 1989). Οι δάσκαλοι και τα σχολικά εγχειρίδια κατά συνέπεια θα πρέπει να συνδέουν τον επίσημο συμβολισμό των κλασμάτων με τις ανεπίσημες γνώσεις των παιδιών αλλά και με συγκεκριμένα μοντέλα. Μια γνωστική προσέγγιση στη διδασκαλία των κλασμάτων μπορεί να κάνει το αντικείμενο ενδιαφέρον, να το κάνουν να έχει νόημα για τους μαθητές του δημοτικού ώστε να αποτελέσει μια στερεή βάση για την επέκταση της διδασκαλίας (Baroody, 1989).
Νοηματοδότηση της έννοιας του κλάσματος: Τα κλάσματα αναφέρονται τόσο σε συνεχείς (μοιράζω μία τούρτα) όσο και σε ασυνεχείς ποσότητες (μοιράζω 20 καραμέλες). Οι έννοιες που σχετίζονται με τα κλάσματα είναι πολύπλοκες. Υπάρχουν δύο βασικές κύριες έννοιες οι οποίες μπορούν να βοηθήσουν στην κατανόηση όλων των παραμέτρων. Αυτές είναι οι έννοιες του διαχωρισμού και της ισοδυναμίας. Ο διαχωρισμός αφορά τη διαδικασία της ίσης μοιρασιάς και η ισοδυναμία αφορά τους διαφορετικούς τρόπους με τους οποίους μπορεί να παρασταθεί η ίδια ποσότητα (π.χ. 1/2 = 2/4 = 3/6 κλπ. ) (Reys et al, 1989). Τα δεκαδικά κλάσματα αναπαριστούν διαχωρισμούς σε δεκάδες, εκατοντάδες κλπ. ενώ τα κοινά κλάσματα μπορεί να αναπαριστούν οποιονδήποτε διαχωρισμό. Τα κοινά κλάσματα είναι πιο γενικά από τα δεκαδικά και μπορεί να αρχίσει κανείς τη διδασκαλία με αυτά αλλά αυτό δεν υπονοεί ότι η συνολική μελέτη των κοινών κλασμάτων θα πρέπει να ολοκληρωθεί πριν ασχοληθεί κανείς με τα δεκαδικά κλάσματα. Αν έχει προηγηθεί μια βασική θεμελίωση της έννοιας των κλασμάτων τότε μπορεί να πραγματοποιηθεί η εισαγωγή των δεκαδικών κλασμάτων. Πολλές από τις λειτουργίες των δεκαδικών κλασμάτων είναι ευκολότερες από τις αντίστοιχες λειτουργίες με τα κοινά κλάσματα και μπορούν κατά συνέπεια να διδαχθούν με τρόπο που να έχει νόημα πριν ολοκληρωθεί η διδασκαλία των λειτουργιών με τα κοινά κλάσματα (Reys et al, 1989). Τρεις διακριτές έννοιες των κλασμάτων συνήθως εμφανίζονται στα προγράμματα των δημοτικών σχολείων. Η σχέση μέρους-όλου, το πηλίκο και η αναλογία. Το βάρος δίνεται κυρίως στη σχέση μέρους-όλου και οι δύο άλλες έννοιες αναπτύσσονται ελάχιστα.
Σχέση μέρους-όλου (συνεχείς και ασυνεχείς ποσότητες): Σχέση μέρους-όλου (περιοχή) Ένα κλάσμα όπως τα 3/5 σηματοδοτεί τα τρία μέρη μιας εννιαίας περιοχής χωρισμένης σε πέντε ίσα μέρη όπως φαίνεται για παράδειγμα στο παρακάτω σχήμα. Τετράγωνα, κύκλοι και ορθογώνια είναι σχήματα που μπορούν εύκολα να διαχωριστούν σε ίσα τμήματ
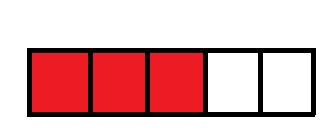
Σχέση μέρους-όλου (μήκος) Μια μονάδα μήκους μπορεί να χωριστεί σε κλασματικές μονάδες. Τα παιδιά μπορούν να διπλώσουν μακριές και στενές λωρίδες χαρτιού στη μέση, σε τρίτα, τέταρτα κλπ. Τέτοιου τύπου δραστηριότητες παρέχουν σημαντική βοήθεια για την τοποθέτηση των κλασμάτων στην αριθμογραμμή, δραστηριότητα κατά την οποία τα παιδιά συναντούν σημαντική δυσκολία.
Σχέση μέρους-όλου (ασυνεχείς ποσότητες). Αυτό το μοντέλο χρησιμοποιεί το σύνολο μιας ποσότητας ως την αρχική μονάδα. Αυτό το μοντέλο παρουσιάζει δυσκολίες για τα παιδιά καθώς αυτά πολλές φορές δεν έχουν σκεφτεί π.χ. τα 20 αντικείμενα ως μία μονάδα. Επίσης αν τα παιδιά δεν έχουν εργαστεί με αντικείμενα και εισαχθούν απευθείας στο συμβολισμό, οι δυσκολίες είναι μεγαλύτερες. Η μονάδα εδώ αποτελείται από 9 αντικείμενα και τη χωρίζουμε σε τρίτα.

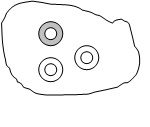
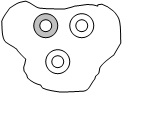
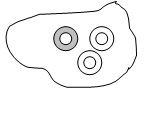
Σχέση μέρους όλου (επιφάνεια) Το μοντέλο αυτό αναπαράστασης είναι εξειδικευμένο, περιλαμβάνει την έννοια της περιοχής και πρέπει να έρθει σε επόμενο στάδιο. Ο εκπαιδευτικός απομακρύνει τον περιορισμό ότι τα τμήματα πρέπει να έχουν οπωσδήποτε το ίδιο σχήμα. Αυτό που χρειάζεται μόνο να έχουν τα σχήματα είναι να έχουν την ίδια επιφάνεια.
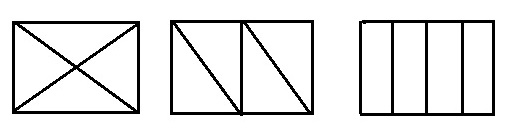
Πηλίκο: Ένα κλάσμα όπως τα 3/5 μπορεί να θεωρηθεί και ως πηλίκο της αντίστοιχης διαίρεσης. Ένα πρόβλημα που θα αντιστοιχούσε σε αυτή τη διαίρεση θα ήταν το εξής: «Αν τρεις σοκολάτες μοιραστούν σε 5 παιδιά, πόση σοκολάτα θα έπαιρνε το κάθε παιδί». Ένα τέτοιο πρόβλημα μπορεί να παρασταθεί ως εξής:
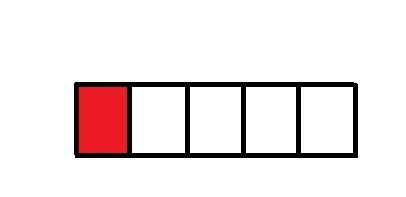


Κάθε παιδί θα έπαιρνε το 1/5 από κάθε σοκολάτα κατά συνέπεια 3 δια 5 = 3/5
Αναλογία: Το κλάσμα 3/5 μπορεί να νοηθεί και ως αναλογία. Ένα μοντέλο θα ήταν τρία λυπημένα παιδιά για κάθε πέντε χαρούμενα παιδιά. Αυτή είναι μια εντελώς διαφορετική ερμηνεία της έννοιας του κλάσματος και δεν θα μας απασχολήσει εδώ. (Reys et al, 1989)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Ανάπτυξη της έννοιας του κλάσματος στα παιδιά: O Piaget με τους συνεργάτες του ξεκίνησε την έρευνα για την κατανόηση των κλασμάτων από τα παιδιά, ζητώντας από αυτά να χωρίσουν ολόκληρες ποσότητες σε ίσα μέρη –δύο, τρία, τέσσερα, πέντε και έξι- και στη συνέχεια να αποφανθούν για την ισοδυναμία α) του όλου και του αθροίσματος των μερών και β) δύο ίδιων ποσοτήτων οι οποίες έχουν μοιραστεί σε διαφορετικά μέρη. Η υπόθεσή τους ήταν ότι για να καταφέρουν τα παιδιά το διαχωρισμό του όλου σε ίσα τμήματα, θα πρέπει να έχουν κατανοήσει ποια είναι η σχέση του όλου με τα μέρη και ότι αυτή η κατανόηση έχει άμεση σχέση με τη διατήρηση του όλου ανεξάρτητα από τον αριθμό των διαχωρισμών τους οποίους έχει αυτό υποστεί. Οι δραστηριότητες αφορούσαν το μοίρασμα ενός κέικ σοκολάτας σε κούκλες. Αυτά που παρατηρήθηκαν ήταν τα εξής: τα παιδιά των τεσσάρων και πέντε ετών απέτυχαν στις προσπάθειές τους να χωρίσουν τη συνολική ποσότητα σε ένα προκαθορισμένο αριθμό ισοδύναμων μερών. Κατά την ηλικία όμως των έξι και επτά ετών, που επιτυγχάνεται η διατήρηση του όλου, τα παιδιά ήταν ικανά να αντιληφθούν τη σχέση ανάμεσα στο όλο και στα μέρη και μπορούσαν να χωρίσουν το σύνολο σε έναν προκαθορισμένο αριθμό, κατά προσέγγιση ίσων, μερών. Αυτά τα αποτελέσματα οδήγησαν τον Piaget και τους συνεργάτες του να συμπεράνουν ότι η κατανόηση των κλασμάτων συνδέεται άμεσα με την κατανόηση της διατήρησης του όλου. (Nunes & Bryant, 1996).
Ο Lima σε μία έρευνα με παιδιά 7 – 12 ετών από τη Βραζιλία επέκτεινε την έρευνα του Piaget βάζοντας τα παιδιά να εργαστούν τόσο με συνεχείς όσο και με ασυνεχείς ποσότητες. Τα ευρήματα της έρευνας επιβεβαίωσαν τα ευρήματα του Piaget και των συνεργατών του δείχνοντας ότι η ισοδυναμία ανάμεσα σε ισοδύναμα κλάσματα που εμφανίζονταν όμως οπτικά με διαφορετικούς τρόπους, κατανοούνταν από τα παιδιά μόνο σε σχέση με την ανάλυση των σχέσεων όλου σε συνάρτηση με τα μέρη. Ο διαχωρισμός δε των ασυνεχών ποσοτήτων γινόταν κατανοητός πριν από το διαχωρισμό συνεχών ποσοτήτων. (Nunes & Bryant, 1996).
Οι παραπάνω έρευνες περιγράφουν μια οπτιμιστική εικόνα της κατανόησης της έννοιας του κλάσματος από τα παιδιά. Άλλες έρευνες όπως του Hart και της Kerslake δίνουν μια εντελώς διαφορετική εικόνα. Η Kerslake για παράδειγμα αναφέρει ότι ακόμα και παιδιά 12 – 14 ετών είχαν δυσκολίες να σειροθετήσουν κλάσματα και να τα τοποθετήσουν πάνω στην αριθμογραμμή. Σε σχέση με την τελευταία δραστηριότητα, μόνο ένα από τα 15 παιδιά που έλαβαν μέρος στην έρευνα μπόρεσε να τοποθετήσει σωστά το κλάσμα 2/3 και μόνο τρία από τα 15 παιδιά μπόρεσαν να τοποθετήσουν σωστά το κλάσμα ½. (Nunes & Bryant, 1996). Και άλλοι ερευνητές υποστηρίζουν ότι οι έννοιες που σχετίζονται με τα κλάσματα δεν αναπτύσσονται επαρκώς μέχρι την ηλικία των 9 ετών. (Reys et all, 1989)
Η ερμηνεία που έδωσαν οι Nunes & Bryant για να εξηγήσουν τις τόσο διαφορετικές επιδόσεις των μαθητών στις διαφορετικές έρευνες, αναφέρεται στην αποσύνδεση που υπάρχει ανάμεσα στην επίσημη μαθηματική γνώση που διδάσκεται στα σχολεία και την κατανόηση των καθημερινών καταστάσεων από τα παιδιά. Οι συγγραφείς υποστηρίζουν ότι όταν τα παιδιά εμπλέκονται σε πειραματικές καταστάσεις σκέφτονται πάνω σε αυτές με λογικούς τρόπους. Αντίθετα όταν λύνουν μαθηματικά προβλήματα στο σχολείο, ερμηνεύουν την κατάσταση, ως μία κατάσταση όπου θα πρέπει να σκεφτούν ποιες διαδικασίες να ακολουθήσουν με τους αριθμούς και πώς να χρησιμοποιήσουν αυτά που έχουν μάθει στο σχολείο. Η επικέντρωση στο χειρισμό των μαθηματικών συμβόλων οδηγεί τα παιδιά στο να αποδώσουν τελικά σε χαμηλότερο επίπεδο από ότι θα απέδιδαν αν συγκεντρώνονταν στην κατάσταση την οποία αντιπροσωπεύει το πρόβλημα. (Nunes & Bryant, 1996).
Πώς δημιουργείται όμως αυτό το κενό ανάμεσα στην κατανόηση των αριθμών που εκφράζουν αναλογίες και στην επίδοση των παιδιών σε δραστηριότητες που απαιτούν συμβολισμούς; Η απάντηση ίσως βρίσκεται στο γεγονός ότι οι τελευταίες απαιτούν ένα διαφορετικό είδος γνώσης που είναι πιο αφηρημένο. Ο Streefland αναφέρει ότι ο τύπος των προβλημάτων που χρησιμοποιούνται στη διδασκαλία μπορεί να παίζει καθοριστικό ρόλο στη μάθηση. Τα προβλήματα θα πρέπει να περιλαμβάνουν δύο μεταβλητές οι οποίες να μπορούν και οι δύο να αναπαρασταθούν. Αντί να χωρίζει κανείς μία πίτσα σε κάποια τμήματα και να διδάσκει στους μαθητές τα κλάσματα, θα πρέπει να τους θέτει προβλήματα όπου και οι δύο μεταβλητές να μπορούν να παρασταθούν. Ένα παράδειγμα τέτοιου τύπου προβλήματος είναι το εξής: «Σε μία συγκέντρωση του σχολείου αναμένεται να έρθουν 30 γονείς και σε κάθε τραπέζι μπορούν να καθίσουν έξι γονείς. Πόσα τραπέζια χρειαζόμαστε;». Ένα τέτοιο πρόβλημα μπορεί εύκολα να παρασταθεί από τα παιδιά. Αν τα παιδιά ενθαρρύνονται να συζητούν και να συγκρίνουν τις λύσεις που δίνουν, τότε θα μπορέσουν να κατανοήσουν τις αντιστοιχίες στις διαδικασίες και θα συνδέσουν την εξωσχολική γνώση με την επίσημη συμβολική γλώσσα.
Συνοψίζοντας τα παραπάνω μπορεί να πει κανείς ότι όταν τα παιδιά ενθαρρύνονται να λύνουν προβλήματα χρησιμοποιώντας τις ανεπίσημες γνώσεις τους και τις συμβολικές αναπαραστάσεις, μπορούν να κάνουν τις απαραίτητες συνδέσεις αυθόρμητα σε μια σχετικά περιορισμένη χρονικά περίοδο διδασκαλίας. Τα προβλήματα αυτά πρέπει να αφορούν τόσο συνεχείς όσο και ασυνεχείς ποσότητες, όπου και οι δύο μεταβλητές μπορούν με σαφήνεια να παρασταθούν, η ποσότητα που πρέπει να μοιραστεί και ο αριθμός των αποδεκτών. Αν η αναπαράσταση των κλασμάτων εισαχθεί με αυτόν τον τρόπο τότε τα παιδιά θα δουν τη σύνδεση των δύο (Nunes & Bryant, 1996).
Συνήθεις δυσκολίες και λάθη των μαθητών: Κατά την ενασχόληση των μαθητών με τα κλάσματα παρατηρούνται ορισμένα λάθη και παρανοήσεις τα οποία είναι πολύ συνηθισμένα στον μαθητικό πληθυσμό και προδίδουν ελλιπή κατανόηση των σχετιζόμενων εννοιών. Ο εκπαιδευτικός θα πρέπει να αδράξει κυριολεκτικά την ευκαιρία και να εκμεταλλευτεί τα λάθη των μαθητών προκειμένου να τα αναδείξει και δημιουργήσει τις συνθήκες που θα επιτρέψουν στα παιδιά να διασαφήσουν τις ιδέες τους.
Ένα από τα πιο συχνά λάθη που κάνουν οι μαθητές με τα κλάσματα είναι να μην αναγνωρίζουν ότι ένα κλάσμα αποτελεί ένα τμήμα ίσων σε μέγεθος τμημάτων. Ένα δεύτερο λάθος, είναι να επιλέγουν ως μεγαλύτερο το κλάσμα που έχει τον μεγαλύτερο παρονομαστή. Σε αυτή την περίπτωση, καθώς τα παιδιά δεν έχουν κατανοήσει τις εμπλεκόμενες έννοιες, εφαρμόζουν λανθασμένα τους κανόνες σύγκρισης των ακεραίων αριθμών στα κλάσματα (Baroody, 1989). Επίσης τα παιδιά δυσκολεύονται να κατανοήσουν ότι υπάρχει διαφορά ανάμεσα στο κλάσμα μιας ποσότητας και στο κλάσμα μιας ομάδας αντικειμένων. Μπερδεύουν για παράδειγμα το ¼ από τέσσερις πίτες με το ¼ μίας πίτας. Αυτό δεν είναι παράξενο καθώς στα παιδιά δίνονται κυρίως αναπαραστάσεις μόνο συνεχών ποσοτήτων (Baroody, 1989).
Ισοδύναμα κλάσματα: Οι μαθητές έχουν ιδιαίτερη δυσκολία με τα ισοδύναμα κλάσματα, την ιδέα δηλαδή ότι διαφορετικά κλάσματα μπορεί να αναπαριστούν την ίδια ποσότητα (Anderson & Wong, 2007). Η κατανόηση της ισοδυναμίας είναι σημαντική καθώς αποτελεί τη βάση για την κατανόηση της πρόσθεσης και της αφαίρεσης των κλασμάτων και επιτρέπει στους μαθητές να συγκρίνουν και να σειροθετούν κλάσματα. (Kamii, Clark, 1995). Η έννοια του κλάσματος του μισού είναι ίσως η πιο εύκολη από όλες, καθώς προσφέρει στα παιδιά τη δυνατότητα να χρησιμοποιήσουν λογικές σχέσεις τις οποίες ήδη κατανοούν και κατά συνέπεια ο εκπαιδευτικός θα έπρεπε να αρχίσει από αυτή ώστε να μπορέσει να βοηθήσει τους μαθητές να επεκτείνουν τη γνώση τους και να κατανοήσουν την έννοια της ισοδυναμίας. (Nunes & Bryant, 1996).
Γενίκευση εννοιών: Πολύ συχνά παρατηρείται το φαινόμενο τα παιδιά να μην μπορούν να προχωρήσουν από μόνα τους στη γενίκευση μίας έννοιας. Στη γεωμετρία για παράδειγμα μερικά παιδιά δεν κατανοούν την ιδέα ότι μία γωνία αποτελείται από γραμμές που εκτείνονται απεριόριστα από ένα σημείο. Μια ημιτελώς ανεπτυγμένη έννοια μπορεί να αναπτυχθεί σε περίπτωση που παρουσιάζονται στα παιδιά μόνο οξείες για παράδειγμα γωνίες. Αν ένα παιδί αναπτύξει μία τέτοιου τύπου κατανόηση για τις γωνίες μπορεί να μη θεωρεί ότι μια ορθή ή μία αμβλεία γωνία είναι γωνίες. (Baroody, 1989)
Για να αποφύγουμε τέτοιους περιορισμούς στη σκέψη των παιδιών μπορούμε να τους παρέχουμε πολλαπλές αναπαραστάσεις των εννοιών. Οι πολλαπλές αναπαραστάσεις μπορούν να βοηθήσουν τους μαθητές να αναπτύξουν μια ευρύτερη και βαθύτερη κατανόηση των κλασμάτων. (Baroody, 1989) Σε πρωταρχικό επίπεδο τα διαφορετικά επίπεδα σχήματα παρέχουν μια ιδανική εισαγωγή τόσο για τη γεωμετρία και τα κλάσματα όσο και για τη λύση προβλημάτων.(Baroody, 1989)
Ο ρόλος της γεωμετρίας στην ανάπτυξη των μαθηματικών εννοιών: Ένας από τους ρόλους των δραστηριοτήτων γεωμετρίας είναι να εμπλουτίσουν τις ικανότητες αντίληψης χώρου των μαθητών. Οι δεξιότητες που έχουν σχέση με την αντίληψη του χώρου περιλαμβάνουν πολλές πλευρές της κατανόησης του περιβάλλοντος, όπως το να αντιλαμβανόμαστε και να φτιάχνουμε εικόνες και ζωγραφιές, να σχηματίζουμε νοητικές εικόνες και να μπορούμε να αντιληφθούμε νοητικά κίνηση και αλλαγές σε αυτές τις εικόνες. (Young, 1987) Οι ικανότητες που έχουν να κάνουν με το χώρο είναι ιδιαίτερα σημαντικές καθώς η γνώση μας για τον κόσμο επηρεάζεται από την αντίληψη, από το πώς μεταφράζουμε και οργανώνουμε τα οπτικά ερεθίσματα. Κατά δεύτερο λόγο πολλά μαθήματα στην αριθμητική (αλλά και σε άλλα αντικείμενα) χρησιμοποιούν εικόνες και φυσικά αντικείμενα και πρέπει να ερμηνευτούν με συγκεκριμένους τρόπους. (Young, 1987)
Έρευνες όπως αυτή των Gay και McDaniel αναφέρουν θετική σχέση ανάμεσα στο επίπεδο επιτυχίας στα μαθηματικά και στις ικανότητες αντίληψης χώρου σε μαθητές δημοτικού σχολείου. (Gay & McDaniel, 1977). Επίσης, στο βιβλίο του δασκάλου της Ε’ τάξης του δημοτικού (σελ 10) αναφέρεται ότι «Η γεωμετρία χρησιμοποιείται σε πολλές περιπτώσεις είτε ως διδακτικό πλαίσιο γνώσης είτε ως υπόβαθρο διαισθητικής κατανόησης άλλων εννοιών πχ. πολλαπλασιασμός κλασμάτων, διαίρεση ομωνύμων κλασμάτων, ισοδύναμα κλάσματα, δεκαδικοί αριθμοί».
Για τους παραπάνω λόγους επιλέξαμε το υλικό που χρησιμοποιούμε στις διδασκαλίες να εμπεριέχει στοιχεία γεωμετρίας. Ακόμα το δεύτερο μέρος της τρίτης διδασκαλίας (το οποίο αφορά μετατροπές κλασμάτων από δέκατα σε εκατοστά για να καταλήξει στην πρόσθεση ετερώνυμων κλασμάτων) παρομοιάζει δραστηριότητες παζλ καθώς γίνεται προσπάθεια τα παιδιά να βρουν αντιστοιχίες ανάμεσα σε διάφορα κομμάτια. Όταν οι μαθητές ασχολούνται με δραστηριότητες παζλ και φαντάζονται ποιο κομμάτι ταιριάζει σε ποια θέση πριν το χρησιμοποιήσουν, αυτό αποτελεί μια νοητική διαδικασία σημαντική για να αναπτυχθούν χωρικές ικανότητες. (Young, 1987)
Ο ρόλος των εικαστικών στη μάθηση: Κάποιες από τις δραστηριότητες που προτείνονται στις διδασκαλίες συνδυάζουν τη χρήση των εικαστικών με τη διδασκαλία των μαθηματικών εννοιών. Στα πλαίσια των νέων Α.Π. που προωθούν τη διαθεματικότητα και την οριζόντια σύνδεση των μαθημάτων κάτι τέτοιο δεν είναι απλώς αποδεκτό αλλά αναγκαίο. Στις σελίδες 3827-3828 του ΦΕΚ τεύχος β’ Αρ. φύλλου 303, 13 Μαρτίου 2003 αναφέρονται οι άξονες, γενικοί στόχοι και οι θεμελιώδεις έννοιες της διαθεματικής προσέγγισης: να μπορεί ο μαθητής «Να χρησιμοποιεί την τέχνη, για να συμπληρώνει άλλα μαθήματα», «Να χρησιμοποιεί τις εικαστικές τέχνες διαθεματικά με τα άλλα μαθήματα» και «Να χρησιμοποιεί τις γνώσεις του για τις εικαστικές τέχνες στα άλλα μαθήματα» για τις τάξεις Α-Β, Γ-Δ, Ε-ΣΤ αντίστοιχα.
Είναι γνωστό ότι το ιχνογράφημα και η ενασχόληση του παιδιού με τη ζωγραφική εμφανίζεται ως αυθόρμητη δραστηριότητα κατά την οποία το παιδί αντλεί την ευχαρίστησή του από το γεγονός ότι την αντιμετωπίζει σαν παιχνίδι (Μπέλλας, 2000). Επίσης η γενική αρχή των ενισχυτών δραστηριοποίησης, που είναι γνωστή ως «αρχή» του Premack, ορίζει ότι μια συμπεριφορά η οποία εμφανίζεται συχνά και αυτόνομα και κατά συνέπεια έχει ευχάριστες συνέπειες μπορεί να χρησιμοποιηθεί για να ενισχυθεί μια άλλη συμπεριφορά που εμφανίζεται σπάνια και όχι ευχάριστα. (Κολιάδης, 1996). Συνδυάζοντας τα παραπάνω επιλέξαμε, μέσω του υλικού που προτείνουμε, να δώσουμε την ευκαιρία στα παιδιά να βάψουν τμήματα εικόνων καθιστώντας τις δραστηριότητες με τον αυτό πιο ευχάριστες για τα ίδια.
Έχει γίνει προσπάθεια, οι τέσσερις διδασκαλίες που παρουσιάζονται εδώ, να σχεδιαστούν με παιγνιώδη μορφή, καθώς είναι γνωστό ότι το παιδί που κάθεται να παίξει ένα οργανωμένο παιχνίδι χαλαρώνει και ταυτόχρονα συγκεντρώνεται. Χαλαρώνει, γιατί το παιχνίδι είναι διασκεδαστικό και συγκεντρώνεται γιατί το παιχνίδι περιέχει δυσκολίες και προσκλήσεις. Κατά συνέπεια το παιδί που βρίσκεται σε αυτή την κατάσταση, βρίσκεται στην ιδανική κατάσταση για να μάθει. (Πέγκυ Κέυ, 1996) Επίσης, οι δραστηριότητες σχεδιάστηκαν κατά τρόπο ώστε να πραγματεύονται λίγους και πολύ συγκεκριμένους μαθησιακούς στόχους κάθε φορά. Εκτός από τις δυσκολίες που μπορεί να προκαλέσει η πολλαπλότητα των στόχων στην μάθηση, είναι προφανές ότι όσο περισσότεροι είναι οι στόχοι και οι προαπαιτούμενες γνώσεις κάθε φορά, τόσο πιο εξειδικευμένο είναι το υλικό. Όσο πιο εξειδικευμένο είναι το υλικό σε τόσο μικρότερο ποσοστό των παιδιών απευθύνεται. Στόχος μας είναι να παράγουμε ένα υλικό το οποίο να μπορεί να χρησιμοποιηθεί από το σύνολο των μαθητών.
Ακόμα γίνεται προσπάθεια μέσα από τις διαφορετικές δραστηριότητες να δοθούν ευκαιρίες στα παιδιά να προσεγγίσουν τη νέα γνώση με διερευνητικό και ομαδικό τρόπο. Στις οδηγίες των διδασκαλιών που αναφέρονται στον εκπαιδευτικό αναφέρεται ποιες δραστηριότητες είναι σχεδιασμένες για να πραγματοποιηθούν σε ομάδες και σε ποιες οι μαθητές εργάζονται ατομικά. Επίσης ορισμένες από τις δραστηριότητες εμπεριέχουν και διαθεματικά στοιχεία όπως για παράδειγμα η εργασία της σειροθέτησης κλασμάτων στους πύργους του Eiffel και στο Big Ben στη δεύτερη διδασκαλία και οι μετατροπές και πρόσθεση απλών δεκαδικών κλασμάτων μέσα από διαφορετικούς τύπους επίστρωσης πλακών στην τρίτη διδασκαλία (παραδοσιακός φλαμανδικός τύπος, ρωμαϊκός τύπος), που επιτρέπουν επεκτάσεις ή συνδέσεις με άλλα θέματα από τον εκπαιδευτικό.
Ακόμα, καθώς η αξιολόγηση αποτελεί βασικό στάδιο κάθε οργανωμένης και συστηματικής διαδικασίας (Κωνσταντίνου, 2002) και προκειμένου να διαπιστωθεί ο βαθμός επίτευξης των αρχικά σχεδιασμένων στόχων, ως τελική μορφή αξιολόγησης στο τέλος των τεσσάρων διδασκαλιών προβλέπονται οκτώ φύλλα εργασίας σε ηλεκτρονική μορφή μέσω του προγράμματος excel. Η επιλογή της ηλεκτρονικής μορφής για το σχεδιασμό αξιολόγησης έγινε τόσο για να προστεθεί ποικιλία στο υπάρχον υλικό αλλά και γιατί ο υπολογιστής έχει αναδειχθεί σε δυναμικό εκπαιδευτικό εργαλείο καθώς παρέχει άμεση ανάδραση στο χρήστη και προκαλεί την άμεση εμπλοκή του στη μαθησιακή διαδικασία. Το γεγονός ότι παρέχει άμεση δυνατότητα αυτοδιόρθωσης είναι ιδιαίτερα σημαντικό, καθώς η αποστέρηση από τις ευκαιρίες αυτοδιόρθωσης θεωρείται μία από τις πολλές αιτίες τις σχολικής υστέρησης και αποτυχίας. (Ράπτη & Ράπτη, 2004). Προτείνουμε στους εκπαιδευτικούς σε όσα φυλλάδια αναφέρονται ονόματα παιδιών να τα αντικαθιστούν με ονόματα παιδιών της τάξης τους. Κάτι τέτοιο βοηθά να δημιουργηθεί κλίμα οικειότητας στην τάξη και τα παιδιά αντιμετωπίζουν με περισσότερο ενδιαφέρον και πολύ καλύτερη διάθεση τις δραστηριότητες.
Πρώτη Πορεία Διδασκαλίας
Με τη συγκεκριμένη διδασκαλία στοχεύουμε οι μαθητές να: Κατανοούν, διαβάζουν και να γράφουν τα δεκαδικά κλάσματα, και συγκεκριμένα τα δέκατα, και να κατανοήσουν ότι το ίδιο κλάσμα μπορεί να αναπαρασταθεί με διαφορετικούς τρόπους.
Προαπαιτούμενες γνώσεις: Οι μαθητές θα πρέπει να γνωρίζουν τι συμβολίζει ο παρονομαστής και ο αριθμητής στα κλάσματα. (προβλέπεται από τη Β’ Δημοτικού)
Υλικό: Μαρκαδόροι για τους μαθητές
Οδηγίες προς τον εκπαιδευτικό
Ι. Ο εκπαιδευτικός διερευνά αν οι μαθητές θυμούνται από τις προηγούμενες τάξεις ποια λειτουργία επιτελούν ο αριθμητής και ο παρονομαστής στα κλάσματα. Τονίζει ότι στα κλάσματα ο διαχωρισμός του όλου γίνεται σε ίσα μέρη. Μία έκφραση που «πιάνει» στα παιδιά είναι «η μοιρασιά πρέπει να είναι δίκαιη». Ανάλογα με το επίπεδο της τάξης ο εκπαιδευτικός θα χρειαστεί να αφιερώσει εδώ περισσότερο ή λιγότερο χρόνο.
ΙΙ. Ο εκπαιδευτικός δίνει το πρώτο φυλλάδιο με τους φύλακες του βασιλιά, συζητά με τους μαθητές σε πόσα τμήματα είναι χωρισμένη η κάθε ασπίδα και αφήνει τους μαθητές να ολοκληρώσουν τη δραστηριότητα σύμφωνα με τις οδηγίες του φυλλαδίου. Οι μαθητές εργάζονται ατομικά.
ΙΙΙ. Ο εκπαιδευτικός δίνει το δεύτερο φυλλάδιο και οι μαθητές το ολοκληρώνουν σύμφωνα με τις οδηγίες που αναφέρονται σε αυτό. Ο εκπαιδευτικός μπορεί να σημειώσει διαφορετικά δεκαδικά κλάσματα για κάθε μαθητή στο σημείο που προβλέπεται στο φύλλο εργασίας. Οι μαθητές εργάζονται ατομικά αλλά το φυλλάδιο εμφανίζεται σε τρεις διαφορετικές μορφές ώστε να μοιραστούν τρία διαφορετικά φυλλάδια σε κάθε ομάδα για να τονιστούν έτσι οι διαφορετικοί τρόποι με τους οποίους μπορούν να παρασταθούν τα ίδια κλάσματα.
IV. Στο τέλος του μαθήματος και αν έχει μείνει χρόνος (κάτι που εξαρτάται από την πρώτη φάση) μπορούν να κοπούν οι φιγούρες από τα φυλλάδια και να κολληθούν σε χαρτόνι κανσόν ανάλογα με τον αριθμό που δηλώνει το κάθε κλάσμα. Αυτό θα μπορούσε να αναχθεί και σε ομαδική δραστηριότητα, η κάθε ομάδα δηλαδή να έχει ετοιμάσει δέκα φύλακες με ασπίδες από 1/10 ως 10/10.
Σύνδεση με τη θεωρία: Πολλαπλές αναπαραστάσεις της έννοιας του κλάσματος σε ασυνεχείς ποσότητες, Πολλαπλή αναπαράσταση του ίδιου κλάσματος.
Δεύτερη πορεία διδασκαλίας
Με τη συγκεκριμένη διδασκαλία στοχεύουμε οι μαθητές να: Κατανοούν, διαβάζουν και να γράφουν τα δεκαδικά κλάσματα, και συγκεκριμένα τα δέκατα, τα εκατοστά και τα χιλιοστά και να μπορούν να σειροθετούν απλά δεκαδικά κλάσματα.
Προαπαιτούμενες γνώσεις: Οι μαθητές θα πρέπει να είναι ικανοί να ορίζουν σημεία και να τραβούν ευθείες γραμμές με το χάρακα. (προβλέπεται από τη Β’ Δημοτικού)
Υλικό: Μαρκαδόροι, χάρακας, μολύβι, κόλλα, ψαλίδι για τους μαθητές, Μιλιμετρέ χαρτί, κομμένο σε διάσταση 10Χ10 για τον εκπαιδευτικό, σε τόσα κομμάτια όσα και οι μαθητές της τάξης.
Οδηγίες προς τον εκπαιδευτικό:
Ι. ο εκπαιδευτικός δίνει το πρώτο φυλλάδιο και συζητά με τους μαθητές πώς θα χωρίσουν το λευκό τετράγωνο-χαλί σε 10 ίσα τμήματα. Οι μαθητές συμπληρώνουν το φυλλάδιο σύμφωνα με τις οδηγίες. Οι μαθητές εργάζονται ατομικά.
ΙΙ. Ο εκπαιδευτικός δίνει το δεύτερο φυλλάδιο και ζητά από τους μαθητές να μετρήσουν σε πόσα κουτάκια είναι χωρισμένο το νέο τετράγωνο-χαλί. Κάνουν συγκρίσεις σε σχέση με το πρώτο τετράγωνο. Στη συνέχεια ο εκπαιδευτικός ρωτά τα παιδιά: «Αφού χωρίσαμε το πρώτο χαλί σε 10 κουτάκια, το δεύτερο σε 100, σε πόσα λέτε να χωρίσουμε το τελευταίο;» Ο εκπαιδευτικός αφήνει τους μαθητές να δοκιμάσουν να το χωρίσουν σε 1.000 κουτάκια και καθώς αυτοί θα διαπιστώσουν ότι κάτι τέτοιο είναι ιδιαίτερα δύσκολο, τους προμηθεύει με τα κομμάτια από το μιλιμετρέ χαρτί τα οποία έχει ήδη έτοιμα κομμένα. Οι μαθητές κολλούν το μιλιμετρέ χαρτί πάνω στο λευκό τετράγωνο και προβαίνουν και πάλι σε συγκρίσει με τα δύο προηγούμενα τετράγωνα. Οι μαθητές βάφουν το 1/100 του πρώτου τετραγώνου και το 1/1000 του δεύτερου και στη συνέχεια σειροθετούν τις κλασματικές μονάδες. Οι μαθητές εργάζονται ατομικά.
ΙΙΙ. Ο εκπαιδευτικός δίνει το επόμενο φυλλάδιο με τους πύργους και ζητά από τα παιδιά να τοποθετήσουν τα κλάσματα που εμφανίζονται μέσα στα συννεφάκια με σειρά από το μικρότερο (στη βάση του πύργου) προς το μεγαλύτερο (στην κορυφή) ή και αντίστροφα. Οι μαθητές εργάζονται ομαδικά και ο εκπαιδευτικός τους προτρέπει να χρησιμοποιήσουν τα φυλλάδια με τα τετράγωνα-χαλιά για να κάνουν τις απαραίτητες συγκρίσεις σε περίπτωση διαφωνίας ή αμφιβολίας. Στο τέλος οι απαντήσεις επιβεβαιώνονται στον πίνακα ώστε να γνωρίσουν τα παιδιά τις σωστές απαντήσεις και να εξηγηθούν τα λάθη. Είναι προφανές ότι ο εκπαιδευτικός μπορεί να σημειώσει στα σύννεφα ευκολότερα ή δυσκολότερα να σειροθετηθούν κλάσματα.
Επέκταση: Η σειροθέτηση κλασμάτων αποδεικνύεται ιδιαίτερα δύσκολη δραστηριότητα για τα παιδιά όχι τόσο όταν πρόκειται για σειροθέτηση κλασμάτων μεταξύ τους αλλά όταν πρόκειται για την εύρεση της θέσης τους στην αριθμογραμμή. Η δεύτερη δραστηριότητα θα απαιτούσε κανονικά το σχεδιασμό ειδικού μαθήματος όπου θα ζητούνταν από τα παιδιά να τοποθετήσουν τόσο απλά, όσο και καταχρηστικά κλάσματα (μεγαλύτερα της μονάδας π.χ. 8/5) στην αριθμογραμμή. Στην προκειμένη περίπτωση ο εκπαιδευτικός θα μπορούσε απλώς να ζητήσει από τα παιδιά να τοποθετήσουν πάνω σε μία μεγάλη αριθμογραμμή που θα σχεδίαζε στον πίνακα (και η οποία θα περιλάμβανε τις υποδιαιρέσεις μιας απλής μονάδας) τα κλάσματα που επέλεξε να σημειώσει στα συννεφάκια του τρίτου φύλλου εργασίας.
Σύνδεση με τη θεωρία: Συνήθη λάθη μαθητών,Συγκρίσεις κλασμάτων.
Τρίτη Πορεία διδασκαλίας
Με τη συγκεκριμένη διδασκαλία στοχεύουμε οι μαθητές να: Κατανοήσουν ότι η ίδια ποσότητα μπορεί να εκφραστεί με διαφορετικά κλάσματα και να μπορέσουν να κάνουν απλές μετατροπές και προσθέσεις δεκαδικών κλασμάτων.
Προαπαιτούμενες γνώσεις: Γνώση του πίνακα πολλαπλασιασμού του 2 και του 10.
Υλικό: Μαρκαδόροι, ψαλίδι, κόλλα
Οδηγίες προς τον εκπαιδευτικό:
Ι. Ο εκπαιδευτικός δίνει στους μαθητές το πρώτο φυλλάδιο. Οι μαθητές το συμπληρώνουν σύμφωνα με τις οδηγίες. Αφού το συμπληρώσουν και βρουν ποιο κλάσμα κάθε φορά αντιπροσωπεύει καλύτερα το σχήμα τους, ο εκπαιδευτικός σημειώνει όλα τα κλάσματα στον πίνακα για να τονίσει ακριβώς ότι το «μισό» μπορεί να γραφεί με διαφορετικούς τρόπους. Τα κλάσματα που θα προκύψουν είναι προφανώς τα ½, 3/6, 4/8, 5/10, 6/12, και 7/14.
ΙΙ. Ο εκπαιδευτικός δίνει το επόμενο φυλλάδιο (2ο) στο οποίο οι συνολικές ποσότητες είναι μονοί αριθμοί και όχι ζυγοί όπως στο προηγούμενο. Εδώ προκύπτει το ζήτημα πώς θα βαφεί η μισή ποσότητα (κάποιο σχήμα θα πρέπει να βαφεί το μισό) και πώς γραφεί το αντίστοιχο κλάσμα.(η μετατροπή σε κλάσμα με ζυγό παρονομαστή είναι η αναγκαστική λύση). Ο εκπαιδευτικός συντονίζει την συζήτηση και ζητά προτάσεις-λύσεις από τους μαθητές. Τα κλάσματα που προφανώς θα προκύψουν είναι με σειρά από αριστερά προς τα δεξιά τα: 3/6, 5/10, 7/14, 5/10, 11/22, 9/18.
ΙΙΙ. Ο εκπαιδευτικός δίνει τα επόμενα δύο φυλλάδια (3ο και 4ο) στους μαθητές. Η εργασία είναι ομαδική. Το 3ο φυλλάδιο προορίζεται για να κοπεί από τους μαθητές για να συμπληρωθούν τα σχήματα στο 4ο φυλλάδιο. Στο 4ο φυλλάδιο εμφανίζονται δύο διαφορετικοί τρόποι επίστρωσης πλακών: ο πρώτος είναι ο παραδοσιακά Φλαμανδικός ενώ ο δεύτερος τρόπος χρησιμοποιούνταν κατά τους ρωμαϊκούς χρόνους (Rawson, 1990). Οι μαθητές καλούνται να αναγνωρίσουν ποιο τμήμα ανήκει σε ποιο τρόπο (σχήμα), να κόψουν τις αντίστοιχες επιφάνειες από το 3ο φυλλάδιο, να τις κολλήσουν πάνω στα κενά σχήματα και τέλος να υπολογίσουν με κλάσματα ποια είναι η συνολική επιφάνεια. Στο πρώτο σχήμα το κλάσμα που προκύπτει είναι τα 49/10 ενώ στο δεύτερο 6/10 ή 60/100.
Προέκταση: Αν ο εκπαιδευτικός επιθυμεί να εξασκήσει περισσότερο τους μαθητές του στις μετατροπές κλασμάτων από δέκατα σε εκατοστά και το αντίστροφο όπως και στα αθροίσματα δεκαδικών κλασμάτων μπορεί να προτείνει στους μαθητές της εξής δραστηριότητα: Ο κάθε μαθητής μπορεί να δημιουργήσει ένα μοτίβο με βάση τα σχήματα που έχει και να το δώσει στη συνέχεια στον διπλανό του για να υπολογίσει σε άθροισμα πόσα δέκατα ή εκατοστά περιέχει. Τέτοια παραδείγματα μοτίβων θα μπορούσαν να είναι τα παρακάτω και θα αντιστοιχούσαν σε 38/100 και 36/100 το πρώτο και δεύτερο αντίστοιχα. Οι μαθητές θα παράγουν απλούστερα ή συνθετότερα μοτίβα ανάλογα με τις ικανότητές τους.
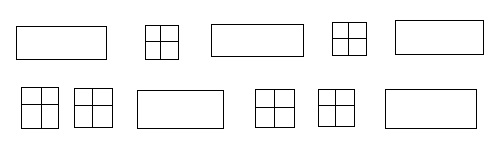
Σύνδεση με τη θεωρία:Εισαγωγή στις διακριτές ποσότητες, Έννοια του μισού, Ισοδύναμα κλάσματα, Μετατροπές και πρόσθεση απλών κλασμάτων
Τέταρτη Πορεία Διδασκαλίας
Με τη συγκεκριμένη διδασκαλία στοχεύουμε οι μαθητές να: Μπορέσουν να υπολογίσουν το κλάσμα ενός αριθμού.
Προπαιτούμενες γνώσεις: Να πολλαπλασιάζουν και να διαιρούν με το 10 και το 100.
Υλικό: Μαρκαδόροι
Οδηγίες προς τον εκπαιδευτικό:
Ι. Ο εκπαιδευτικός δίνει το πρώτο φυλλάδιο με τους φύλακες στους μαθητές και οι μαθητές το συμπληρώνουν σύμφωνα με τις οδηγίες που αναφέρονται σε αυτό. Ο εκπαιδευτικός καταγράφει στον πίνακα τα αποτελέσματα. Μπορεί να καταγράψει ολόκληρη τη σειρά αριθμών στον πίνακα: (δηλαδή τα 2/10 του 10, τα 2/10 του 20, τα 2/10 του 30, τα 2/10 του 40, τα 3/10 του 10, τα 3/10 του 20, τα 3/10 του 30, τα 3/10 του 40, τα 4/10 του 10, τα 4/10 του 20, τα 4/10 του 30, τα 4/10 του 40 κλπ. έτσι ώστε να μπορέσει να συζητήσει και κατά συνέπεια να οδηγήσει τους μαθητές να διατυπώσουν τον κανόνα (δηλαδή διαιρώ τον αριθμό με το 10 – τον παρονομαστή- και πολλαπλασιάζω στη συνέχεια με τον αριθμητή). Παρότι τα παιδιά βρίσκουν εύκολα το αποτέλεσμα η λεκτική διατύπωση του κανόνα από μέρους τους αποδεικνύεται ότι απαιτεί αρκετό χρόνο. Ο εκπαιδευτικός μπορεί να βοηθήσει τα παιδιά προτρέποντάς τα να του πουν με ποιον τρόπο θα εξηγούσαν σε κάποιο μικρότερο παιδί πώς βρίσκουν κάθε φορά το αποτέλεσμα. Έχει βρεθεί ότι τα παιδιά είναι πιο εκφραστικά και ευκρινή σε ένα ρόλο όπου φαντάζονται ότι βοηθούν κάποιο μικρότερο και με λιγότερες γνώσεις από τα ίδια. (Hughes, 1996). Όταν οι μαθητές διατυπώσουν τον κανόνα, ο εκπαιδευτικός οπωσδήποτε τον καταγράφει στον πίνακα και τα παιδιά με τη σειρά τους στο φυλλάδιο εργασίας.
ΙΙ. Ο εκπαιδευτικός δίνει το δεύτερο φυλλάδιο στους μαθητές το οποίο περιλαμβάνει απλές ασκήσεις. Οι μαθητές εργάζονται ομαδικά και υπολογίζουν το αποτέλεσμα των ασκήσεων. Το αποτέλεσμα που βρίσκουν κάθε φορά τους οδηγεί να ενώσουν να ενώσουν τις τελίτσες που φαίνονται στο φυλλάδιο. Το σχήμα που προκύπτει είναι ένα καράβι. Το φυλλάδιο παρέχει με αυτό τον τρόπο τη δυνατότητα άμεσης ανατροφοδότησης στους μαθητές.
Επέκταση: Η εφαρμογή του κανόνα μπορεί να πάρει λίγο χρόνο για να εμπεδωθεί ο εκπαιδευτικός μπορεί να δώσει περισσότερες ασκήσεις στους μαθητές. Ο συνδυασμός της κατανόησης με την εξάσκηση στις μαθηματικές πράξεις φαίνεται να παράγει τα καλύτερα μαθησιακά αποτελέσματα. (Cole, Cole, 2001)
Σύνδεση με τη θεωρία: Ασυνεχείς ποσότητες
Τα φύλλα αξιολόγησης: Οδηγίες προς τον εκπαιδευτικό: Ως συνοδευτικό υλικό για το κλείσιμο των τεσσάρων διδασκαλιών παρέχεται ένα απλό πρόγραμμα οκτώ φύλλων εργασίας στο πρόγραμμα excel (βλ. αρχείο εργασίας). Τα φύλλα αξιολόγησης αντιστοιχούν ανά δύο στους στόχους των τεσσάρων διδασκαλιών. Μπορείτε να μπείτε στο πρόγραμμα μέσα από την υπερσύνδεση που θα βρείτε παρακάτω ή κανονικά από το αρχείο που υπάρχει μέσα στον αρχικό φάκελο. Όταν θα είστε μέσα στο πρόγραμμα μπορείτε να κινηθείτε από το ένα φύλλο εργασίας στο άλλο κάνοντας «κλικ» με το ποντίκι πάνω στους δείκτες των φύλλων εργασίας που εμφανίζονται στο κάτω αριστερό μέρος της οθόνης. Οι μαθητές πρέπει να γράψουν τις απαντήσεις τους στο κίτρινο κουτάκι με ΚΕΦΑΛΑΙΑ γράμματα και να πατήσουν στη συνέχεια enter. Αν η απάντηση που έχουν δώσει είναι η σωστή στο κουτάκι που υπάρχει ακριβώς από κάτω εμφανίζεται η φράση «ΜΠΡΑΒΟ». Αν η απάντηση των παιδιών είναι λανθασμένη εμφανίζεται η φράση «ΠΡΟΣΠΑΘΗΣΕ ΞΑΝΑ». Οι σωστές απαντήσεις στα οκτώ φύλλα εργασίας είναι αντίστοιχα:
|
Φ.Ε. 1ο |
ΤΡΙΑ (Πρόκειται για τα κλάσματα 4/10, 2/5, 8/20) |
|
Φ.Ε. 2ο |
ΤΕΣΣΕΡΑ (Πρόκειται για τα κλάσματα ½, 5/10, 4/8, 6/12) |
|
Φ.Ε. 3ο |
ΕΠΤΑ ΔΕΚΑΤΑ |
|
Φ.Ε. 4ο |
ΤΕΣΣΕΡΑ ΤΕΤΑΡΤΑ |
|
Φ.Ε. 5ο |
Η ΕΛΕΝΗ |
|
Φ.Ε. 6ο |
Ο ΣΑΚΗΣ |
|
Φ.Ε. 7ο |
Ο ΝΙΚΟΣ, Ο ΑΛΕΚΟΣ, Ο ΧΡΗΣΤΟΣ (5/10, 6/20=3/10, 6/30=2/10) |
|
Φ.Ε. 8ο |
Ο ΠΕΛΑΡΓΟΣ, Ο ΒΑΤΡΑΧΟΣ, ΤΟ ΛΙΟΝΤΑΡΙ, ΤΟ ΑΛΟΓΟ (99/1000 είναι περίπου 1/10, 3/10, 68/100, 7/10) |
Anderson, J., Wong, M. (2007). Teaching Common Fractions in Primary School: Teachers' Reactions to a New Curriculum. AARE's 36th Annual International Education Research Conference - Adelaide 2006, Melbourne: Australian Association for Research in Education (AARE)
Baroody, A. J. (1989). Manipulatives don't come with guarantees. Arithmetic Teacher, 37(2), 4-5.
Hughes, M. (1986). Children and Number: Difficulties in Learning Mathematics. Cornwall: Wiley-Blackwell.
Kamii, C., Clark, F. B. (1995). Equivalent fractions: Their difficulty and educational implications. The Journal of Mathematical Behavior, 14, 365-378.
Nunes, T., Bryant, P. (2007) Τα παιδιά κάνουν μαθηματικά. επιμέλεια Δ. Δεσλή (Επιμέλ.). Σ. Λειβαδοπούλου, Γεωργία Σαρηγιαννίδου (Μεταφρ.). Σ. Βοσνιάδου (Επιμελ. Σειράς). Αθήνα : Gutenberg - Γιώργος & Κώστας Δαρδανός.
Reys, R. E., Suydam, M. N., & Lindquist, M. M. (1989). Helping children learn mathematics. Englewood Cliffs, N.J.: Prentice Hall.
Van de Walle, J. A. (2005). Μαθηματικά για το δημοτικό και το γυμνάσιο: Μια εξελικτική διδασκαλία. Τ. Α. Τριανταφυλλίδης. (επιμ.). Α. Αλεξανδροπούλου & Β. Κομπορόζος. (μεταφ.). Αθήνα: Τυπωθήτω.
Young, P. (1987). The nature of information. New York: Praeger.
Κολιάδης, Ε. Α. (1997). Θεωρίες μάθησης και εκπαιδευτική πράξη: Γνωστικές θεωρίες. Αθήνα: Ελληνικά Γράμματα.
Κολιάδης, Ε. Α. (2002). Γνωστική ψυχολογία, γνωστική νευροεπιστήμη και εκπαιδευτική πράξη: Μοντέλο επεξεργασίας πληροφοριών. Αθήνα : Ιδιωτική έκδοση.
Ματσαγγούρας, Η. (2000). Ομαδοσυνεργατική Διδασκαλία και Μάθηση. Αθήνα: Γρηγόρης
Τριλιανός, Θ. Α. (2000). Μεθοδολογία της Σύγχρονης ∆ιδασκαλίας. Καινοτόμες επιστημονικές προσεγγίσεις στη ∆ιδακτική Πράξη. Αθήνα: Ιδιωτική Έκδοση