Γεωμετρία και Τέχνες
Submitted by ltme on Wed, 04/22/2015 - 09:25
Είναι γεγονός ότι υπάρχουν αμφιβολίες όσον αφορά τη σχέση των μαθηματικών και της τέχνης και κατά πόσον αυτή υφίσταται. Κι αυτό γιατί τα μαθηματικά είναι μια επιστήμη, η οποία ασχολείται με το λογικό μέρος του μυαλού, εκείνο που κατά κάποιο τρόπο περιορίζεται και «εγκλωβίζεται» σε συγκεκριμένα γεγονότα που δεν μπορούν παρά να έχουν μια και μόνο κατάληξη, ένα και μόνο αποτέλεσμα, βασισμένο σε θεωρίες, πράξεις και κυρίως έννοιες που παραμένουν σταθερές κι απαράλλακτες στο βάθος των αιώνων. Από την άλλη, η τέχνη δεν πρόκειται για μια επιστήμη. Πρόκειται για την απελευθέρωση της φαντασίας, την υποκειμενικότητα και αφορά κυρίως το συναισθηματικό μέρος του μυαλού. Δεν τίθεται θέμα περιορισμού, αλλά δίνει περιθώρια ελευθερίας έκφρασης και τοποθέτησης της προσωπικής πινελιάς του ατόμου χωρίς να εκλαμβάνεται κάτι ως σωστό ή λανθασμένο. Τα πάντα είναι δεκτά χωρίς να είναι απαραίτητα κατανοητά κι αποδεκτά από όλους. Παρόλα αυτά, η τέχνη και τα μαθηματικά είναι δυο έννοιες που σχετίζονται άμεσα μεταξύ τους και συγκεκριμένα, η γεωμετρία και η τέχνη. Πόσες φορές έχουμε δει έργα τέχνης να κοσμούνται από οριζόντιες, κάθετες ή διαγώνιες γραμμές; Πόσο συχνά έχουμε παρατηρήσει ανθρώπους με στρογγυλά κεφάλια, τρίγωνα φορέματα, παραλληλόγραμμα παντελόνια, τετράγωνα σπίτια και διαμάντια-ρόμβους να στολίζουν τις παιδικές ζωγραφιές; Εκεί, λοιπόν, κρύβεται η αλληλεπίδραση της τέχνης με τη γεωμετρία, μια σχέση όχι τόσο ιδιόμορφη όσο πιστεύει κανείς, αλλά πολύ δυνατή ώστε να επηρεάζει η μια την άλλη και μαζί να βγάζουν ένα πανέμορφο αποτέλεσμα.

Η ιστορία του κουκλοθέατρου:Αναμφισβήτητα το κουκλοθέατρο αποτελεί ένα σημαντικό μέσο ψυχαγωγίας και διαπαιδαγώγησης του παιδιού, δίνοντας του ερεθίσματα για συναισθηματική κινητοποίηση, καλλιτεχνική συγκίνηση και χαρά. Παίζει ακόμη και ρόλο κοινωνικοπολιτικό αφού το μέλλον κάθε λαού είναι τα σημερινά παιδιά που με τη γνώμη τους και τη βούληση τους θα είναι οι θεμελιωτές και οι ρυθμιστές της τύχης της χώρας τους. Μέχρι να φτάσει το κουκλοθέατρο στη σημερινή του μορφή πέρασε από πολλά στάδια. Η τάση για μίμηση ξεκίνησε αρχικά στον άνθρωπο με μικρές κινήσεις του χεριού που εξελίχθηκαν σε μιμικές κινήσεις παραστατικότερες. Στα παλιά τα χρόνια ο άνθρωπος πριν από την εποχή του Καίσαρα, στον Μεσαίωνα έφτιαχνε ανδρείκελα. Το ομοίωμα του αποτέλεσε τη πρώτη άπλαστη μορφή θεατρικού είδους. Τα χρησιμοποιούσαν στις αναπαραστάσεις των παθών και σε άλλες θρησκευτικές εκδηλώσεις οι οποίες στάθηκαν αφορμή να ονομαστούν marionettes από το όνομα της Παναγίας ( Marie- Marion- Marionette ). Αυτή η μορφή κουκλοθέατρου αποτέλεσε θέαμα και στις αγορές στις γιορτές και στα πανηγύρια. Η ιδιορρυθμία των ανδρείκελων με την αναλλοίωτη έκφραση τους, το στυλιζάρισμα της ανθρώπινης κίνησης, τα φανταχτερά χρώματα των κουστουμιών, η έντονη σκηνική δράση δημιουργούσαν κάτι το εντυπωσιακό που ασκούσε ένα είδος μαγείας στο μεγάλο ακροατήριο των δρόμων αιχμαλωτίζοντας τα βλέμματα μικρών και μεγάλων. Αυτή είναι η πρωτόγονη μορφή του κουκλοθέατρου η οποία όμως διώχτηκε. Κατά την Αναγέννηση επικρατεί η ιταλική κωμωδία με μάσκες. Γνωστός εδώ είναι ο Πουλτσινέλο ο καμπούρης ή ο κακομούτσουνος. Τον 18ο αιώνα το κουκλοθέατρο ακμάζει και μπαίνει πλέον στα παλάτια ψυχαγωγώντας τους άρχοντες. Τον 19ο αιώνα εισέρχεται σε όλη την Ευρώπη και στην Ασία και οι παραστάσεις του έχουν μεγάλη επιτυχία. Έτσι με το διάβα των αιώνων το κουκλοθέατρο έφτασε στην σημερινή του μορφή που πλέον οι επικρατέστεροι φορείς του δυστυχώς είναι μόνο οι παιδαγωγοί.
Ιστορία του κολάζ: Τα παιδιά από την στιγμή που έρχονται στον κόσμο, προσπαθούν να γνωρίσουν, να ανακαλύψουν το περιβάλλον τους και όσο μεγαλώνουν να δημιουργούν. Όπως οι "μεγάλοι" μετά από πολλές έρευνες έχουν και συνεχίζουν να φτιάχνουν είτε χρήσιμα αντικείμενα π.χ. παιχνίδια, πράγματα για το σπίτι καθημερινής χρήσης, Μ.Μ.Μ. (αυτοκίνητα, μηχανές, αεροπλάνα) είτε έργα τέχνης(πίνακες, γλυπτά και άλλα) έτσι και τα παιδιά αποτελούν τους μικρούς δημιουργούς. Ένας από τους τρόπους δημιουργίας εικαστικών είναι η τέχνη του κολάζ. Εκτός όμως από το ενδιαφέρον τους για καλλιτεχνικές δημιουργίες έχουν ανάγκη για γνώση, για μία πρώτη επαφή με τα γράμματα,τους αριθμούς κ.λ.π. Το κολάζ λοιπόν αποτελεί έναν τρόπο συνδυασμού των τεχνών με τις γνώσεις όπως των εικαστικών με τα μαθηματικά. Στην προκειμένη περίπτωση το κολάζ με τα γεωμετρικά σχήματα. Όταν αναφερόμαστε στο κολάζ εννοούμε την παράσταση μιας μορφής ή μιας εικόνας με την επικόλληση διαφόρων υλικών. Είναι μια μορφή τέχνης που βασίζεται στον κυβισμό και στον Ντανταϊσμό και καθιερώθηκε τα χρόνια του Μεσοπολέμου. Οι πρώτοι που εφάρμοσαν την τεχνική της πρόσθεσης ξένων υλικών στο έργο τέχνης για να αποτελέσουν ένα ενιαίο σώμα ήταν ο Μπρακ και ο Πικάσο. Όταν ανακαλύφθηκε η πρωτόγονη, για τότε, τεχνική αποτέλεσε κίνητρο για την δημιουργία καινούργιων μορφών. Μπορούμε να συναντήσουμε διάφορα είδη αυτής της τεχνικής όπως Κολάζ: από φύλλα, σε στυλ παζλ, από τυχαία σχήματα, με προοπτική, από διπλωτική σε ανάγλυφα, ψηφιδωτά και χαρτοδιπλωτική σε κολαζ. Τα παιδικά έργα χαρακτηρίζονται από τον αυθορμητισμό, την ψυχική και συναισθηματική έκφραση, την αγνότητα, την πρωτοτυπία για αυτό και τα υλικά που χρησιμοποιούμε είναι ελεύθερα και ανεξάρτητα από τι παριστάνουν στην πραγματικότητα π.χ. ένα φτερό που μπορεί να γίνει δέντρο, δεν υπάρχουν κανόνες. Τα υλικά μπορεί να είναι ό,τι βρίσκεται στην διάθεσή μας όπως: χαρτιά, σακούλες, υφάσματα, μέταλλα, πέτρες, φύλλα και πολλά ακόμη. Έτσι κι αλλιώς το κολάζ είναι θέμα φαντασίας, μπορούμε το ίδιο θέμα να το αποδώσουμε με διαφορετικούς τρόπους. Αναφερθήκαμε παραπάνω στις πρώτες επαφές των παιδιών με τα μαθηματικά. Αυτό μπορεί να επιτευχθεί μέσα από το κολάζ δημιουργώντας σε ένα χαρτόνι κάποιο τοπίο και στην συνέχεια να τοποθετούμε χαρτονάκια γεωμετρικών σχημάτων πάνω στα σχέδια. Με αυτόν τον τρόπο τα παιδιά γνωρίζουν τα σχήματα, αρχίζουν πλέον να τα αναγνωρίζουν, δηλαδή το τετράγωνο, το ορθογώνιο, το τρίγωνο, τον κύκλο.
Υφαντική: Από παλιά η τέχνη της υφαντικής συσχετιζόταν άμεσα με τα γεωμετρικά μοτίβα. Πολλά ήταν τα υφαντά που απεικόνιζαν γεωμετρικά σχήματα( τρίγωνα, τετράγωνα, κύκλους, παραλληλόγραμμα κ.ά.) είτε πάνω σε χαλιά, είτε πάνω σε παραδοσιακές ενδυμασίες, είτε πάνω σε κεντητά τραπεζομάντηλα ή διακοσμητικά κεντητά που τοποθετούνταν σε διάφορα μέρη του σπιτιού. Οι εικόνες, λοιπόν, των διαφόρων γεωμετρικών μοτίβων είναι γνώριμες σε αρκετούς, αφού πολλά από τα παραπάνω παραμένουν μέχρι και σήμερα στη μόδα( τα χαλιά που κοσμούν τα σπίτια μας απεικονίζουν σε μεγάλο μέρος τους γεωμετρικά σχήματα)! Σε γενικές γραμμές, η τέχνη της υφαντικής σχετίζεται άμεσα με τη γεωμετρία και τα μοτίβα της. Τα πρώτα βήματα στον κόσμο της τέχνη αυτής έγιναν με το κέντημα σχημάτων πάνω σε λευκά υφάσματα από τους Αιγυπτίους και στη συνέχεια αναπτύχθηκε ακόμα περισσότερο κι από άλλους λαούς, οι οποίοι συνέχισαν να ασχολούνται και να υφαίνουν γεωμετρικά μοτίβα, συμπληρώνοντας τη δική τους σφραγίδα. το κέντημα είναι ένας πολύ καλός τρόπος να εισάγουμε τα παιδιά στον κόσμο των μαθηματικών και συγκεκριμένα στα γεωμετρικά σχήματα και, παράλληλα ένας τρόπος διασκεδαστικός, ακίνδυνος- αρκεί να υπάρχει η επίβλεψη τους εκπαιδευτικού- και που αφήνει περιθώρια να δημιουργήσουν το δικό τους μοτίβο, με το δικό τους μοναδικό τρόπο.


Γεωπίνακας: Ο γεωπίνακας αποτελεί έναν μια σύγχρονη προσέγγιση των μαθηματικών στην προσχολική εκπαίδευση, αλλά και έναν δημιουργικό και αποτελεσματικό τρόπο να κατανοήσουν τα παιδιά τις μαθηματικές έννοιες και να κάνουν τα πρώτα τους βήματα στον κόσμο των γεωμετρικών σχημάτων. Οι γεωπίνακες αποτελούν ένα από τα καλύτερα μέσα για την αναπαράσταση δισδιάστατων σχημάτων. Κυρίως χρησιμοποιούνται για την ανάπτυξη της γεωμετρικής σκέψης των παιδιών και αποτελεί εξαιρετική μέθοδο για την κατασκευή γεωμετρικών σχημάτων από τα παιδιά με εύκολο και διασκεδαστικό τρόπο. Αποτελεί ένα νέο παιχνίδι για τα νήπια, μια νέα πρόκληση και τα βοηθά παράλληλα να κατανοήσουν βαθύτερα το διαχωρισμό των ομάδων των σχημάτων (τρίγωνα, τετράπλευρα, κύκλος) και τα γεωμετρικά μοτίβα που αυτά ανήκουν.

Ιστορία της μουσικής και η έννοια της στοιχειοδομικής μουσικής: Ως μουσική ορίζεται η τέχνη που βασίζεται στην οργάνωση ήχων με σκοπό τη σύνθεση, εκτέλεση και ακρόαση/λήψη ενός μουσικού έργου, καθώς και η επιστήμη που επικεντρώνεται σε θέματα συνδεόμενα με την παραγωγή, οργάνωση και λήψη ήχων, και το σύνολο ήχων από το οποίο απαρτίζεται ένα μουσικό κομμάτι. Η μουσική αναφερόταν παλαιότερα ως Απολλώνια Τέχνη, και παίρνει το τελικό όνομά της από τις εννέα Μούσες της αρχαίας ελληνικής μυθολογίας. Δηλαδή η μουσική διέφερε σημασιολογικά της σημερινής χρήσης του όρου μιας και περιελάμβανε το σύνολο των τεχνών, αφού προστάτης τους ήταν το σύνολο των Μουσών. Σήμερα πάντως η μουσική ως τέχνη, έρχεται να καλύψει την ανάγκη του ανθρώπου να εκφράσει με τους ήχους, τις σκέψεις, τα συναισθήματα και τις ψυχικές του καταστάσεις. Η μουσική χρονολογεί και εξελίσσει την ιστορία της ως παράλληλη μ' εκείνη της Γλώσσας, οπότε και παράλληλα της ανθρώπινης ύπαρξης. Ο άνθρωπος προσπαθεί με τη βοήθεια της μουσικής να καλύψει το φάσμα των αποχρώσεων των υποκειμενικών , προσωπικών σκέψεων και συναισθημάτων που αδυνατεί με τη χρήση της γλώσσας.
Η έννοια της στοιχειοδομικής μουσικής αποτελεί κύριο στοιχείο της εκπαιδευτικής φιλοσοφίας του Carl Orff. Η στοιχειοδομική μουσική πρόκειται για ένα εκπαιδευτικό εργαλείο. Είναι μια περίπλοκη έννοια που μπορεί να κατανοηθεί μόνο από την ανάλυση των επιμέρους στοιχείων της, αλλά πρέπει να λαμβάνονται υπόψη και τα αποτελέσματά στους ανθρώπους καθώς και η αλληλεπίδραση που δημιουργείται ανάμεσα σε ένα πολιτιστικό προϊόν (τη μουσική σύνθεση) και σε αυτούς που το παράγουν. Πρέπει να τονίσουμε ότι δεν αναφερόμαστε απλώς στα στοιχεία της μουσικής όπως οι σκάλες, τα ρυθμικά και τα μελωδικά σχήματα αλλά και στη σχέση που αναπτύσσεται κατά τη διαδικασία της μουσικής πράξης ανάμεσα στον ήχο και τον άνθρωπο. Κατ’ αυτή την έννοια μια μουσική χαρακτηρίζεται ως στοιχείοδομική όχι επειδή είναι εύκολη να ερμηνευτεί αλλά επειδή υπάρχει μια αμοιβαία επίδραση μεταξύ της μουσικής από τη μια μεριά και του ερμηνευτή ή ακροατή από την άλλη. Ο ρυθμός είναι « το στοιχείο εκείνο που ενώνει τη γλώσσα, τη μουσική, και την κίνηση», άποψη του Lane, 1984, που άρχισε να μπαίνει σε εφαρμογή μέσω των ηχηρών κινήσεων (body percussions), όπως για παράδειγμα, παλαμάκια, στράκες με τα δάχτυλα, χτυπήματα ποδιών. Ο ήχος από την άλλη είναι το βασικό υλικό της μουσικής, και όχι η καταγραφή του. μια στοιχειοδομική μουσική πράξη δεν πρέπει να βασίζεται εξ ολοκλήρου στα γραπτά μουσικά κείμενα αλλά να ενθαρρύνει και να απελευθερώνει τη δημιουργική διάθεση της ομάδας που εκφράζεται μέσα από τον αυτοσχεδιασμό. Τα μουσικά κείμενα μπορούν να αποτελέσουν παραδείγματα ή κίνητρα αλλά σε καμιά περίπτωση δεν πρέπει να γίνουν τροχοπέδη στην ανακάλυψη των βασικών στοιχείων της μουσικής και στη δημιουργική τους χρησιμοποίηση μέσω του αυτοσχεδιασμού. Πολλοί είναι οι παιδαγωγοί που θεωρούν τον αυτοσχεδιασμό ζωτικής σημασίας και σπουδαίο εκπαιδευτικό εργαλείο στη διδασκαλία της μουσικής. Ο ίδιος ο Orff δε συνέδεε την εκπαίδευση της μουσικής με τα ταλαντούχα ή έξυπνα παιδιά, αλλά με κάθε παιδί, πιστεύοντας πως κάθε ένα από αυτά είναι εν δυνάμει εκπαιδεύσιμο.
Το αντικείμενο της Ευκλείδιας Γεωμετρίας είναι η μελέτη του χώρου και των σχημάτων, επίπεδων και στερεών, που μπορούν να υπάρξουν μέσα σε αυτόν. Μέσα στο χώρο βρίσκεται ο φυσικός κόσμος, στον οποίο ζούμε, και όλα τα αντικείμενα, μεγάλα ή μικρά, έμψυχα ή άψυχα. Οι επιφάνειες διαχωρίζουν τα αντικείμενα μεταξύ τους ή από το περιβάλλον. Η γεωμετρία ήταν ο πρώτος κλάδος της ανθρώπινης γνώσης που διαμορφώθηκε ως επιστήμη και επί αιώνες ο μόνος. Το αντικείμενό της, ο χώρος και τα σχήματα, είναι και προσιτό και πλούσιο και πρόσφορο για θεωρητική μελέτη αλλά και για πρακτικές εφαρμογές. Από την εποχή του Αρχιμήδη και του Ήρωνα μέχρι σήμερα τα πεδία εφαρμογής της Γεωμετρίας συνεχώς διευρύνονται. Για τα σπίτια που ζούμε, τα καράβια που ταξιδεύουμε, ή τις επεξεργασμένες εικόνες της τηλεόρασης είναι αναγκαία η χρήση της Γεωμετρίας, άμεση ή έμμεση. Η Γεωμετρία ερμηνεύει τις μορφές του περιβάλλοντος χώρου χρησιμοποιώντας λίγες πρώτες αρχές και αξιοποιώντας τη σκέψη και τον ορθό λόγο, προχωράει από το πιο απλό στο πιο σύνθετο. Οι λέξεις κύκλος, τρίγωνο, τετράγωνο, ορθογώνιο παραλληλόγραμμο υπάρχουν σε όλες τις γνωστές γλώσσες, πρόκειται όμως για γνώσεις σκόρπιες, ασύνδετες μεταξύ τους. Η γεωμετρία τις θεμελιώνει, δηλαδή τις οργανώνει σε ένα σύστημα και φυσικά προσθέτει και νέες γνώσεις σε αυτές που ήδη υπάρχουν.
Οι γεωμετρικοί στόχοι για τα παιδιά αναπτύσσονται σε δύο διαφορετικά πλαίσια: τη συλλογιστική σκέψη του χώρου, ή την αίσθηση του χώρου και το συγκεκριμένο περιεχόμενο σε αυτόν. Το πρώτο από αυτά τα δύο πλαίσια αφορά τον τρόπο που σκέφτονται τα παιδιά και τη συλλογιστική τους σκέψη για τα σχήματα και το χώρο. Το δεύτερο πλαίσιο είναι το περιεχόμενο με την πιο παραδοσιακή έννοια, να γνωρίζουμε τις συμμετρίες, τα τρίγωνα, τις παράλληλες γραμμές και άλλα. Σύμφωνα με τον van Hiele υπάρχει ένα χαρακτηριστικό μοντέλο ιεράρχησης πέντε επιπέδων για την κατανόηση των ιδεών του χώρου, ή αλλιώς για τα επίπεδα γεωμετρικής σκέψης. Σε κάθε επίπεδο της γεωμετρικής σκέψης, οι ιδέες που έχουν δημιουργηθεί στα παιδιά γίνονται τα αντικείμενα εστίασης της σκέψης στο επόμενο επίπεδο. Δημιουργείται λοιπόν σύμφωνα με τη θεωρία του van Hiele το εξής σχήμα:
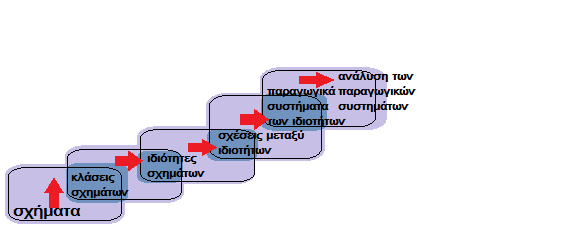
Πρόκειται για τέσσερις διαδραστικές δραστηριότητες που συνδέουν τη γεωμετρία με την τέχνη. Σκοπός μας είναι τα παιδιά μέσα από βιωματικές εμπειρίες να έρθουν σε επαφή με τα γεωμετρικά σχήματα, τα χαρακτηριστικά, τις διαφορές και την ορολογία τους. Με τον τελικό χάρτη εννοιών σε σύγκριση με τον αρχικό βοηθάμε τόσο τα παιδιά να δουν σε τι επίπεδο γεωμετρικών γνώσεων έχουν φτάσει, όσο και εμάς τις ίδιες να συμπεράνουμε κατά πόσο οι δραστηριότητες έχουν επιτύχει τους στόχους τους.
Σύνολο δραστηριοτήτων: Aφόρμηση, κουκλοθέατρο. Kύριο μέρος, υφαντική και κολάζ. Αποθεραπεία, μουσική.
Γενικοί στόχοι: Εισαγωγή των παιδιών στη γεωμετρία. Διάκριση των κατηγοριών των γεωμετρικών σχημάτων. Αναγνώριση των χαρακτηριστικών των γεωμετρικών σχημάτων. Αναγνώριση των χαρακτηριστικών των γεωμετρικών σχημάτων της ίδιας κατηγορίας. Εμπλουτισμός λεξιλογίου με μαθηματικούς όρους.
Δραστηριότητα 1η: Κουκλοθέατρο.
Στόχοι Εμπλουτισμός λεξιλογίου. Αναγνώριση χαρακτηριστικών των σχημάτων. Διάκριση κατηγοριών γεωμετρικών σχημάτων.
Η συγκεκριμένη δραστηριότητα περιλαμβάνει την αρχική γνωριμία των παιδιών με τα σχήματα. Μέσα στον κύκλο συζητάμε με τα παιδιά και τους κάνουμε ερωτήσεις σχετικά με τις γενικές τους γνώσεις για τα γεωμετρικά σχήματα, όπως: « Τι γνωρίζετε για τα σχήματα;», «Ποια σχήματα ξέρετε;», «Ποια είναι τα χαρακτηριστικά τους;», « Πόσα είναι τα σχήματα;» κλπ. Ζητάμε από τα παιδιά να συνδέσουν εικόνες ή αντικείμενα από την τάξη μας, το σπίτι και γενικότερα πράγματα της καθημερινότητάς τους με τα γεωμετρικά σχήματα που γνωρίζουν και όσα μας είπαν προηγουμένως για μια πρώτη επαφή, έτσι ώστε μετέπειτα να έχουμε τη δυνατότητα να συγκρίνουμε τις τωρινές τους γνώσεις με αυτές που θα αποκτήσουν αργότερα και να περάσουμε ομαλά στην ορολογία των σχημάτων. Για αναστοχασμό χρησιμοποιούμε ένα χαρτόνι στο οποίο τα παιδιά γράφουν, ζωγραφίζουν τα σχήματα που ανέφεραν όπως εκείνα τα έχουν στο μυαλό τους.
Δράση εκπαιδευτικού: Η νηπιαγωγός, αφού έχει μαζέψει τα παιδιά στον κύκλο, με μια πολύ απλή ερώτηση («Τι γνωρίζετε για τα σχήματα»), τα εντάσσει στη συζήτηση, μέσα από την οποία αντιλαμβάνονται τις μέχρι τώρα γνώσεις τους για τα γεωμετρικά σχήματα. Τα σχόλιά της είναι κυρίως προτρεπτικά χωρίς να παρεμβαίνει στο λόγο και τις γνώσεις των παιδιών: «Με ποιο σχήμα μοιάζει η σκεπή δηλαδή;», «Όλα τα πιάτα είναι στρογγυλά;» Στη συνέχεια, τα προτρέπει να δημιουργήσουν ένα πίνακα με όσα της είπαν για να μην τα ξεχάσουν και τον τοιχοκολλούν στη γωνιά της παρεούλας. Και κατά τη διάρκεια της δημιουργίας του πίνακα, την κύρια δράση την έχουν τα παιδιά.
Δράση παιδιών: Τα παιδιά, μέσα από την καθοδήγηση της νηπιαγωγού, απαντούν στις ερωτήσεις της και λένε τις δικές τους εμπειρίες, όπως: « Εγώ ξέρω τον κύκλο», « στο δωμάτιο μου έχω μια τετράγωνη κορνίζα», «τα καραβάκια έχουν τρίγωνα πανιά», «Ο ήλιος είναι στρογγυλός» κ.ά. Κατά τη διάρκεια της δημιουργίας του πίνακα, τα παιδιά λένε ιδέες για το πώς να μεταφέρουν όσα είπαν σε αυτόν: «Τον κύκλο να τον κάνουμε ήλιο!», « Το τρίγωνο να το κάνουμε σκεπή από τα σπιτάκια!», « Να κάνουμε και το διαμαντάκι από τα παιχνίδια του υπολογιστή», «Να φτιάξουμε και ένα τετράγωνο μεγάλο δώρο».
Τα υλικά που χρησιμοποιούνται στη συγκεκριμένη δραστηριότητα είναι τα εξής: Χαρτόνι, Μαρκαδόροι, Χαρτοταινία.
Με το πρώτο αυτό μέρος της δραστηριότητας επιτυγχάνουμε να γνωρίζουμε τις μέχρι τώρα γνώσεις των παιδιών για τα σχήματα, και μέσα από τη συζήτηση και μέσα από τη δημιουργία του χαρτονιού, έτσι καταγράφουμε τις αρχικές τους απόψεις για τα σχήματα, για να μπορέσουμε να οδηγηθούμε στο επόμενο μέρος της δραστηριότητας που εμπλουτίζει τις γνώσεις τους.
Οι πρωταγωνιστές στο κουκλοθέατρο που θα παίξουμε είναι: Ο Τετραγωνάκης, ο Παραλληλόγραμμος, το Τραπέζιο, ο Ρόμβος, ο Κύκλος, το Οβάλ, η Ισοσκελής τριγωνούλα, ο Ορθογώνιος τριγωνούλης, ο Σκαληνός τριγωνούλης.

Αρχικά μαζεύουμε τα παιδιά στη γωνιά του κουκλοθέατρου.Εκεί για να τα προετοιμάσουμε τους λέμε ότι σήμερα θα έχουμε στην τάξη μας επισκέπτες, αλλά περίεργους επισκέπτες από μια χώρα μακρινή που λέγεται Σχηματοχώρα, τους ρωτάμε αν θέλουν να τους γνωρίσουν και να αποκτήσουν την προσοχή χτυπάμε δυο φορές τη σκηνή και δε μπαίνει κανείς. Ξεκινάμε με τον τετραγωνάκη.
-Γεια σας, γεια σας …. Ξέρετε από πού είμαι εγώ και ποιος είμαι; Έρχομαι από τη σχηματοχώρα και θέλω πολύ να γνωριστούμε.
-Σςςςςς…..1, 2, 3 απόλυτη ησυχία. Θα σας πω ποιος είμαι αλλά πρώτα θα κάνετε ησυχία!
-Κλείνουν στοματάκια, μαζεύουν ποδαράκια, σταυρώνουν τα χεράκια και ανοίγουν τα ματάκια…
Είμαι ο τετραγωνάκης ζωηρός μα εξυπνάκης. Έχω τέσσερις γωνίες, τέσσερις πλευρές ευθείες. Σε τετράγωνα χαρτάκια γράφω τώρα ποιηματάκια. Ζωγραφίζω και σπιτάκια σε μικρά τετραγωνάκια. Τι ακόμα δε χειροκροτείτε;;; θέλω χειροκρότημα δυνατό, μη νομίζετε πως ήρθα όμως μόνο εγώ. Για περιμένετε να φωνάξω και τον άλλο αδερφό.
(μπαίνει ο Ορθογώνιος Παραλληλόγραμμος με φόρα στη σκηνή) -Εεειιιιι……. Είμαι κι εγώ εδώ και καθίστε να σας πω…. Ο παραλληλόγραμμος είμαι εγώ σχήμα δείτε μοναδικό, όλο χάρη τσαχπινιά μες στη χώρα μου παιδιά. Τέσσερις έχω πλευρές, τέσσερις και οι γωνιές και όλες αυτές ορθές. Μα οι δυο μου οι πλευρές είναι πιο μακριές. Για θαυμάστε με ξανά που έχω τέτοια λεβεντιά…. Τώρα έρχονται και τα άλλα δύο μας αδερφάκια, το Τραπέζιο και ο Ρόμβος!!!
(μπαίνει το Τραπέζιο) -Χαίρεται παιδάκια! Θαυμάστε και το δικό μου σχήμα, για δείτε και εγώ έχω τέσσερις πλευρές, αλλά δεν είναι ορθές. Γέρνω από εδώ, γέρνω από εκεί νομίζετε πως θα πέσω αλλά σας ξεγελώ, γιατί είμαι τόσο σταθερό! Επ! να και ο Ρόμβος!
(μπαίνει ο Ρόμβος) -Να ‘μαι και εγώ! Εγώ είμαι ο Ρόμβος ο Γνωστός με τις τέσσερις κορυφές, βουνό πάνω βουνό κάτω, μια μυτούλα δεξιά μια μυτούλα αριστερά. Σαν τον χαρταετό μπορώ να πετάξω και σαν το διαμαντάκι μεσ’ τη νύχτα να λάμψω! Ποιοι είναι αυτοί που έρχονται στην παρέα μας; Η οικογένεια των κύκλων!
(μπαίνει ο κύκλος) -Ήρθα να σας πω δυο λόγια. Είμαι λίγο ντροπαλός, ντροπαλός μα και σοφός. Ο κύκλος είμαι, στρογγυλός σαν τον ήλιο λαμπερός. Σαν το ολόγιομο φεγγάρι που φωνάζει όλο χάρη. Κύκλος είμαι σαν το πιάτο και του μπουκαλιού τον πάτο. Κύκλος είμαι σαν το κέρμα και του βασιλιά το στέμμα , σαν το βραχιολάκι στης μανούλας το χεράκι. Κύκλος σαν το κουλουράκι και του Μάη το στεφανάκι.
Με είδατε;;; Γωνία δεν έχω καμία ούτε ίση πλευρά. Είμαι ολοστρόγγυλος… Για να δω μπορείτε να κάμετε έναν κύκλο με τα χεράκια σας; Και το άλλο μου το αδερφάκι είναι λίγο ντροπαλό, Οβάλ! Οβάλ! Έλα λίγο από εδώ! Το άλλο μου το αδερφάκι από την οικογένεια των κυκλοειδών!
(μπαίνει διστακτικά ο Οβάλ) -Γεια σας είμαι ο Οβάλ! Σαν κυκλάκι είμαι και εγώ αλλά είμαι λίγο πιο ψηλό, σαν μπαλονάκι μακρουλό, σαν ένα μικρό αυγό. Δεν είμαι όμως όμορφο και εγώ; Ξέρετε πως λέγομαι αλλιώς; Έλλειψη λέγομαι! Το θυμάστε όλοι;
(μπαίνει η ισοσκελής τριγωνούλα)- Ήρθαμε και εμείς η οικογένεια των τριγώνων. Είμαι η ισοσκελής τριγωνούλα μυτερή και πονηρούλα. Σχήμα όμορφο ωραίο μες στον κόσμο τον σπουδαίο. Έχω δείτε τρεις ίσες γωνίες, μη σας φαίνονται αστείες. Σαν βουνό στ’ αλήθεια μοιάζω και από την κορυφή κοιτάζω. Τρεις ίσες γραμμούλες αν ενώσεις ένα τρίγωνο θα δώσεις. Τρεις ίσες γραμμές πλευρές αν γίνουν ένα τρίγωνο σου δίνουν. Τρίγωνα είναι τα ελατάκια, τρίγωνα τα σημαιάκια…. Με ένα τριγωνάκι πίτσα θα γεμίσει η κοιλίτσα.
(μπαίνει ο ορθογώνιος Τριγωνούλης) -Εγώ είμαι ο ορθογώνιος τριγωνούλης ομορφούλης και γλυκούλης. Έχω μια γωνιά ορθή και μια γωνιά πιο ψηλή! Για δείξτε μου όλοι πως είναι αυτή η γωνιά μου, μπορείτε;
(μπαίνει ο Σκαληνός) -Να ‘μαι και εγώ ο Σκαληνός! Τρίγωνο περίεργο μα τρίγωνο συμπαθητικό με λένε όλοι, γιατί τρεις γωνιές και τρεις πλευρές έχω και εγώ αλλά όλες τους διαφορετικές!
Είμαστε πολύ όμορφο σόι. Όπου και να γυρίσετε το κεφάλι σας θα μας δείτε. Για κοιτάξτε όλοι γύρω… Βλέπετε ένα τετράπλευρο; Ένα τρίγωνο; Για ψάξτε να βρείτε ένα κυκλοειδές σχήμα… Είμαστε πολύ σημαντικοί. Η γιαγιά Γεωμετρία μας μαλώνει όπως και εσάς η δική σας γιατί πρέπει να ακολουθούμε κανόνες για να μπορούμε να συνυπάρχουμε. Σας προσκαλούμε να έρθετε στον κόσμο μας να μας γνωρίσετε καλύτερα…. Άλλα ξέρετε τι άλλο; Έχουμε και άλλα αδερφάκια και πολλά ξαδερφάκια, που δεν μπόρεσαν να έρθουν να σας δουν για να προσέχουν τη σχηματοχώρα! Να εμείς τα τριγωνάκια έχουμε αδερφάκια, με πλευρές μικρές μεγάλες, και γωνιές ψηλές κοντές. Και πολλά ξαδερφάκια όχι μόνο με τέσσερις πλευρές όπως τα τετράπλευρα αλλά και περισσότερες που έχουν και πολλές γωνιές!
(μπαίνει ο Κύκλος) - Μα και εγώ έχω και άλλα αδερφάκια , άλλα πιο ψηλά, άλλα πιο κοντά, πιο λεπτά και πιο χοντρά!
Άντε καλέ ένα χειροκρότημα και πάλι για όλους μας….! Και ακόμη ένα για όσους δεν ήρθαν και είναι στη σχηματοχώρα σήμερα!!!
Ο παραπάνω διάλογος δίνει την ευκαιρία στα παιδιά να γνωρίσουν καλύτερα τα διαφορετικά σχήματα, σε ποιες κατηγορίες χωρίζονται, και τα ιδιαίτερα χαρακτηριστικά του καθενός. Με τρόπο διασκεδαστικό και ενδιαφέρον τα παιδιά γνωρίζουν τις βασικές διαφορές των σχημάτων με απώτερο σκοπό να τα ξεχωρίζουν, καθώς και να γνωρίζουν τη μαθηματική τους ονομασία, αλλά και να αναπτύξουν στη φαντασία τους και άλλα σχήματα εκτός από τα συνηθισμένα.
Χρησιμοποιούμε το ίδιο χαρτόνι που χρησιμοποιήσαμε στο Α’ μέρος, το οποίο συμπληρώνουν τα παιδιά με τις νέες πληροφορίες που απέκτησαν για τα σχήματα. Πιο συγκεκριμένα ξεχωρίζουν αρχικά τις διαφορετικές ομάδες των σχημάτων, στη συνέχεια τα διαφορετικά σχήματα που ανήκουν στην ίδια ομάδα, και τέλος μαθαίνουν πως υπάρχουν και άλλα σχήματα πέρα από αυτά που ήδη γνωρίζουν αλλά και την ορολογία τους. Για παράδειγμα: Οικογένεια τριγώνων- Ισοσκελές, Σκαληνό, Ορθογώνιο και άλλα τυχαία τρίγωνα.
Δράση εκπαιδευτικού: Η εκπαιδευτικός αφού μαζεύει τα παιδιά στη γωνιά του κουκλοθέατρου τους λέει «σήμερα ήρθαν στη τάξη μας καινούριοι επισκέπτες, θέλετε να τους γνωρίσετε;». Με αυτό τον τρόπο εισάγει τα παιδιά στην πορεία της δραστηριότητας έτσι ώστενα συμμετέχουν ενεργά στη συζήτηση και να μην είναι παθητικοί δέκτες. Στο εξήςτα παιδιά βοηθιούνται και από άλλες παροτρύνσεις της νηπιαγωγού όπως «μπορείτε να το κάνετε και εσείς αυτό;», « ποιος νομίζετε ότι θα έρθει τώρα;», «για πείτε μου και εσείς με τι μοιάζει αυτό;» κτλ. Ενώ κατά τη διάρκεια συμπλήρωσης του πίνακα καθοδηγεί τα παιδιά στο να μεταφέρουν τα όσα άκουσαν και έμαθαν στο χαρτόνι, για παράδειγμα « για πες μου δηλαδή πόσα είναι τα τρίγωνα που ήρθαν από τη σχηματοχώρα; Υπάρχουν και άλλα εκτός από αυτά; Πώς θα μπορούσαμε να τα ονομάσουμε αυτά τα άλλα;», « μπορείς να τα σχεδιάσεις;» κ.λπ.
Δράσεις παιδιών: Τα παιδιά έπειτα από τις παροτρύνσεις της νηπιαγωγού συμμετέχουν στην δραστηριότητα ενεργά σχηματίζοντας με τα χέρια τους ότι τους ζητάει η νηπιαγωγός, επεμβαίνοντας στη συζήτηση λέγοντας « τώρα θα έρθει η άλλη οικογένεια» ή «αυτό το σχήμαμοιάζει με το βιβλίο μου» «είναι πολλοί δηλαδή στην οικογένεια των τετραπλεύρων!» κτλ. Ακόμη η συμμετοχή τους στη συμπλήρωση του πίνακα κάνει πιο ενεργή τη δράση τους. Αφού έχουν γνωρίσει καλύτερα τα σχήματα το συμπληρώνουν με τα καινούρια πράγματα που έχουν μάθει, κατανοώντας καλύτερα τις γνώσεις τους καταγράφοντάς τες στο χαρτόνι, και προσπαθούν να ονομάσουν τα νέα σχήματα που δημιουργούν.
Για την δραστηριότητα χρησιμοποιούμε τα παρακάτω υλικά: Χαρτόνι, Μαρκαδόροι, Χαρτοταινία.
Για τις κούκλες: Χαρτόνι, Μαρκαδόροι, Ψαλίδι, Κόλλα, Ξύλινα καλαμάκια, Χαρτοταινία.
Με τη συμπλήρωση του χαρτονιού τα παιδιά έχουν κατανοήσει πλέον το γεγονός ότι υπάρχει ποικιλία σχημάτων σε κάθε κατηγορία, καθώς και την ορολογία τους. Στη συνέχεια συγκρίνουμε τις αρχικές τους γνώσεις με αυτές που έχουν κατακτήσει μέχρι τώρα και βλέπουμε τη διαφορά ανάμεσα σε αυτές.
Δραστηριότητα 2η: Κολλάζ με τα γεωμετρικά σχήματα
Στόχοι: Αντιστοίχιση σχημάτων και σχεδίων. Λεπτή κινητικότητα. Αναγνώριση χαρακτηριστικών των διαφορετικών σχημάτων της ίδιας κατηγορίας. Χρήση μαθηματικών όρων.
Σε αυτή τη δραστηριότητα θα δημιουργήσουμε ένα κολλάζ με γεωμετρικά σχήματα. Συγκεντρώνουμε λοιπόν τα παιδιά στη γωνιά της παρεούλας και κάνουμε εισαγωγή στο θέμα με ψευδο-ερωτήσεις όπως «θυμάστε που μας επισκέφτηκαν τα γεωμετρικά σχήματα;», «θα θέλατε να δούμε τη Σχηματοχώρα και πώς φαντάζεστε πως είναι;» Μέσα από αυτή τη δραστηριότητα σκοπός μας είναι να ξεχωρίζουν τα παιδιά τα γεωμετρικά σχήματα και να τα αντιστοιχίζουν με αντίγραφά τους πάνω στο σχέδιο. Έχοντας ζωγραφισμένο ένα χαρτόνι και έτοιμα τα σχήματα τα παιδιά καλούνται να ταιριάξουν πάνω στο κάθε σχέδιο τα κατάλληλα σχήματα. Βέβαια τους δίνουμε τη δυνατότητα να πουν και αυτά τις δικές τους ιδέες και να τις αποτυπώσουν πάνω στο χαρτόνι. Δράση εκπαιδευτικού: Η Νηπιαγωγός για να εισάγει τα παιδιά στη συζήτηση κάνει διάφορες ερωτήσεις όπως «θα θέλατε να δούμε που μένουν τα σχήματα μας;», « πώς φαντάζεστε τη χώρα τους;»κτλ. Έπειτα, χωρίζει τα παιδιά σε ομάδες ανάλογα με τη θέληση τους για να ασχοληθούν με διαφορετικά μέρη του κολάζ. Δηλαδή άλλα να ασχοληθούν με τον ουρανό, άλλα με τα σπίτια, τα δέντρα κλπ. Εφοδιάζει τα παιδιά με χαρτόνια και έτοιμα σχήματα και εξηγεί τη διαδικασία. Αφού ολοκληρωθεί το κολλάζ το τοποθετεί στο τοίχο της γωνιάς των μαθηματικών.

Δράσεις παιδιών: Κατά τη διάρκεια της δραστηριότητας τα παιδιά δίνουν πολλές απαντήσεις αλλά ίσως έχουν και κάποιες πιθανές ερωτήσεις όπως « όλα τα σχήματα μένουν μαζί;», «ποια είναι πιο πολλά;», « και η δικιά μου σκεπή είναι τρίγωνη», «μπορούμε να φτιάξουμε τα σύννεφα με πολλά κυκλάκια;», «γιατί να κάνουμε τις ακτίνες τους ήλιου με τετράπλευρα και όχι με τρίγωνα;» .
Τα υλικά που θα χρησιμοποιήσουμε για την συγκεκριμένη δραστηριότητα είναι τα εξής: Χαρτόνια, Κόλλα, Μαρκαδόροι.
Τα παιδιά τοποθετώντας πάνω στο χαρτόνι τα σχήματα, προσπαθούν να αντιστοιχίσουν τα κομμένα διαφορετικά σχήματα με τα αντίγραφά τους, δείχνοντάς μας με αυτό τον τρόπο κατά πόσο κατανόησαν τα χαρακτηριστικά του κάθε σχήματος, και τις διαφορές μεταξύ τους. Μαθαίνουν επίσης να δημιουργούν με οδηγό τη φαντασία τους τις δικές τους εικόνες με τα νέα σχήματα που έμαθαν.
Σε αυτό το μέρος της δραστηριότητας τα παιδιά καλούνται να ασχοληθούν με την αναγνώριση των διαφορετικών τετραπλεύρων. Πιο συγκεκριμένα να κατανοήσουν τις διαφορές μεταξύ αυτών, και να τα χωρίσουν σε κατηγορίες ΤΕΤΡΑΓΩΝΟ, ΟΡΘΟΓΩΝΙΟ ΠΑΡΑΛΛΗΛΟΓΡΑΜΜΟ, ΡΟΜΒΟΣ, ΤΡΑΠΕΖΙΟ και ΑΠΛΑ ΤΕΤΡΑΠΛΕΥΡΑ. Στο πρόγραμμα GEOGEBRA έχουμε ήδη δημιουργήσει πέντε κουτάκια, και κάτω από αυτά διάσπαρτα διάφορα τετράπλευρα. Τα παιδιά καλούνται να αναγνωρίσουν τα είδη των τετραπλεύρων και τα όμοια εκ των αυτών να τα τοποθετήσουν σε ένα από τα κουτάκια. Από αυτή τη δραστηριότητα επιτυγχάνουμε τα παιδιά να αναγνωρίσουν τις διαφορές των σχημάτων της ίδιας ομάδας (τετραπλεύρων), δίνοντας μεγαλύτερη βάση στα χαρακτηριστικά τους. Βέβαια επειδή είναι δύσκολο να αναγνωρίσουν αμέσως τα σχήματα και τις κατηγορίες τους, τους βάζουμε στην διαδικασία να τα συγκρίνουν με κάποιο που θα αποτελεί το βασικό. Για παράδειγμα, ως πρότυπο χρησιμοποιούμε το τετράγωνο. Παρατηρώντας τα χαρακτηριστικά του βρίσκουμε όσα μοιάζουν με αυτό συγκεντρώνοντας τα και μετά συγκρίνουμε με τα υπόλοιπα σχήματα. Με αυτόν τον τρόπο βλέπουν τις διαφορές και τα όμοια χαρακτηριστικά αυτών μπορούν πιο εύκολα να τα τοποθετήσουν στο κατάλληλο κουτακι. Στη συνέχεια αφού θα τους ζητηθεί να ονομάσουν τα όμοια τετράπλευρα, όπως εκείνα θυμούνται ή νομίζουν, γίνεται συζήτηση σχετικά με τη σωστή ονομασία των σχημάτων αυτών φτάνοντας τελικά σε έναν ακόμη σκοπό μας, να μάθουν τη μαθηματική ονομασία των διαφορετικών τετραπλεύρων.
Δράση εκπαιδευτικού: Μέσω του προγράμματος GEOGEBRA έχουμε δημιουργήσει τα πλαίσια και τα σχήματα με τα οποία θα ασχοληθούν τα παιδιά, αντιστοιχίζοντάς τα. Αναλαμβάνουμε να εξηγήσουμε στα παιδιά τη διαδικασία που θα ακολουθήσουν, «βρείτε ένα σχήμα ώστε να μπορέσουμε να το συγκρίνουμε με άλλα και να βρούμε όσα μοιάζουν», «βλέπετε κάποια σχήματα που να μοιάζουν με αυτό; Μπορείτε να μου πείτε τα όμοια χαρακτηριστικά τους;», «ποιές οι διαφορές τους;» «τοποθετήστε τα σε ένα πλαίσιο- κουτάκι», «τι διαφορές έχουν τα σχήματα σε αυτό το κουτάκι από το διπλανό;» κ.λπ. Διορθώνουμε μέσα από συζήτηση τα λάθη που τυχόν έχουν κάνει, «αυτό το σχήμα δεν έχει τέσσερις ίδιες πλευρές όπως και το διπλανό;», και τους ζητάμε να ονομάσουν την κάθε κατηγορία, δίνοντας αργότερα και τη μαθηματική ονομασία, που τυχόν δε γνωρίζουν.
Δράση παιδιών: Τα παιδιά αρχικά διατυπώνουν κάποιες πιθανές ερωτήσεις όπως «όσα έχουν ίδιες πλευρές να βάλουν το ίδιο κουτάκι; Αυτό που έχει μόνο δύο ίσες είναι διαφορετικό;», «όσα έχουν ίδιο ύψος μπαίνουν στο ίδιο κουτάκι;», «να βάλουμε αυτά που έχουν πλάγιες πλευρές στο ίδιο κουτάκι ή να τα βάλουμε στο άλλο;». Βρίσκονται επίσης στην διαδικασία σύγκρισης των σχημάτων με το πρότυπο. Αφού βρουν όσα έχουν ίδια χαρακτηριστικά τα τοποθετούν στα κουτάκια όπως εκείνα νομίζουν, και με τη βοήθειά μας διορθώνουν τα λάθη τους. Τέλος προσπαθούν να θυμηθούν την ονομασία της κάθε κατηγορίας σύμφωνα με όσα έχουμε πει στις προηγούμενες δραστηριότητες, διατυπώνοντας και δικές τους ιδέες. Για παράδειγμα το ρόμβο μπορεί να το ονομάσουν ΠΛΑΓΙΟ ΤΕΤΡΑΓΩΝΟ.
Τα υλικά που χρησιμοποιούμε στο δεύτερο μέρος της δραστηριότητας είναι ο ηλεκτρονικός υπολογιστής, και το πρόγραμμα GEOGEBRA.
Αρχικά δίνοντας την ευκαιρία στα παιδιά να συγκρίνουν τα σχήματα με το πρότυπο μπορούν με περισσότερη ακρίβεια να κατανοήσουν τα χαρακτηριστικά και να καταλάβουν για ποιο λόγο είναι διαφορετικά. Αφήνοντάς τα να τοποθετήσουν τα σχήματα σε κατηγορίες που τα ίδια σχηματίζουν έχουμε μια πρώτη γνώση για τα όσα έχουν μάθει μέχρι στιγμής. Επισημαίνοντας τα λάθη τους τα κατευθύνουμε ώστε να προσέξουν τα χαρακτηριστικά τους και να δώσουν ιδιαίτερη βαρύτητα στη σύγκριση που ζητάμε να κάνουν μεταξύ τους, για να τα κατηγοριοποιήσουν σωστά. Επιπλέον με την ευκαιρία να δώσουν τα ίδια κάποια ονομασία στα όμοια σχήματα βλέπουμε κατά πόσο έχουν αναγνωρίσει τις διαφορές αυτών και πώς φαίνονται στα δικά τους μάτια. Με αυτόν τον τρόπο και με τη βοήθειά μας εμπλουτίζουν το λεξιλόγιό τους με μαθηματικούς όρους.
Δραστηριότητα 3η: Υφαντική- Γεωπίνακας
Στόχοι: Εξέλιξη της φαντασίας σε σχέση με τα γεωμετρικά σχήματα. Απομόνωση γεωμετρικών σχημάτων από μοτίβα. Απτική δυνατότητα δημιουργίας γεωμετρικών σχημάτων πάνω σε γεωπίνανες.
Η δραστηριότητα αυτή αφορά την υφαντική, μέσα από την οποία θα καταλήξουμε σε ένα πιο πρακτικό μέρος με τη χρήση του γεωπίνακα, πάνω στον οποίο τα παιδιά θα προσπαθήσουν να δημιουργήσουν τα σχήματα που έχουν δει σε προηγούμενες φωτογραφίες, αλλά και σχήματα με δική τους πρωτοβουλία. Αρχικά, έχοντας μαζέψει τα παιδιά στη γωνιά της παρεούλας δείχνουμε στα παιδιά φωτογραφίες υφασμάτων και παραδοσιακών και σύγχρονων ενδυμασιών πάνω στα οποία βρίσκονται διάφορα γεωμετρικά σχήματα και μοτίβα. Τα παιδιά επεξεργάζονται τις φωτογραφίες και ξεκινάει ένας διάλογος ανάμεσα στη νηπιαγωγό και εκείνα σχετικά με τα σχήματα που βλέπουν και τα αναγνωρίζουν. Παράλληλα αναφέρουμε το γεωπίνακα που θα χρησιμοποιήσουμε στη συνέχεια εξηγώντας τον τρόπο και ωθώντας τα παιδιά στη δημιουργία σχημάτων όμοιων με αυτών που έχουμε πει αλλά και δικών τους.
Μετακινούμαστε στη γωνιά των μαθηματικών, όπου χωριζόμαστε σε δύο ομάδες. Στη κάθε ομάδα δίνουμε έναν γεωπίνακα και ξεκινάμε το πρακτικό μέρος της δραστηριότητας μας· ζητάμε από τα παιδιά να προσπαθήσουν να αποτυπώσουν τα σχήματα που παρατήρησαν στις φωτογραφίες με όποιον τρόπο μπορούν. Έπειτα, τους δίνουμε την πρωτοβουλία να σχεδιάσουν πάνω στο γεωπίνακα τα δικά τους σχήματα σύμφωνα με αυτά που έχουν μάθει έως τώρα. Ταυτόχρονα, ζητάμε από τα παιδιά να ονομάζουν το κάθε σχήμα που δημιουργούν και τέλος να χωρίσουν τα σχήματα στις ομάδες που έχουν προαναφερθεί(τρίγωνα, τετράπλευρα, κυκλοειδή). Έχοντας ολοκληρώσει τη δραστηριότητα με το γεωπίνακα η κάθε ομάδα έχει τη δυνατότητα να φτιάξει το δικό της γεωπίνακα με φελιζόλ, με κατάλληλα καρφάκια και ένα μεγάλο λάστιχο. Μέσα από αυτή τη δραστηριότητα στοχεύουμε στο να περάσουν τα παιδιά από τη θεωρία σε ένα λίγο περισσότερο πρακτικό μέρος των μαθηματικών. Επιδιώκουμε να κατανοήσουν ποια είναι τα γεωμετρικά μοτίβα και τον τρόπο που αυτά χωρίζονται σε επιμέρους σχήματα, ανήκοντας παράλληλα στη μεγάλη οικογένεια των γεωμετρικών σχημάτων. Επιπλέον, με τη συγκεκριμένη δραστηριότητα προσπαθούμε να βοηθήσουμε τα παιδιά να εμβαθύνουν στον κόσμο των μαθηματικών και να αρχίσουν να χρησιμοποιούν με ευκολία πλέον μαθηματικές έννοιες(ισοσκελές τρίγωνο, ορθογώνιο παραλληλόγραμμο, τραπέζιο, έλλειψη[οβάλ]κλπ), αλλά και απλή μαθηματική σκέψη, που συμβαδίζει, βέβαια, με την ηλικία τους. Ακόμα έχουν την ευκαιρία να δημιουργήσουν με τα χέρια τους γεωμετρικά σχήματα και να τα παραλλάξουν όπως αυτά θέλουν (πχ τραβούν τα λαστιχάκια και τα τοποθετούν σε διαφορετικά καρφάκια βλέποντας πως μπορούν να δημιουργήσουν μόνα τους τα σχήματα.
Δράση εκπαιδευτικού: Κατά τη διάρκεια της δραστηριότητας μας κάνουμε ορισμένες ερωτήσεις στα παιδιά, ώστε να καταλάβουμε σε τι επίπεδο βρίσκονται ήδη σε σχέση με τα μαθηματικά και, συγκεκριμένα, με τα γεωμετρικά σχήματα. Παραδείγματα τέτοιων ερωτήσεων είναι τα εξής: «Έχετε διακρίνει ποτέ γεωμετρικά σχήματα ή μοτίβα πάνω σε υφάσματα και ρούχα;», «Βλέπετε κάποιο παρόμοιο σχήμα με αυτά που έχουμε μάθει πάνω στα ρούχα που φοράτε;», «Ποια σχήματα διακρίνετε σε αυτές τις φωτογραφίες;», « Πόσα διαφορετικά τετράπλευρα μπορείτε να δείτε σε αυτές τις εικόνες και ποια είναι αυτά;», «Μπορείτε να φτιάξετε τα σχήματα που μόλις είδατε πάνω στο γεωπίνακα μας;», «Θέλετε τώρα να φτιάξετε άλλα παρόμοια σχήματα πάνω στο γεωπίνακα;», «Ελάτε τώρα να φτιάξουμε τους δικούς μας γεωπίνακες!», «Πού πρέπει να βάλουμε τα καρφάκια για να φτιάξουμε ένα ισοσκελές τρίγωνο;», «Πόσα καρφάκια χρειαζόμαστε για να φτιάξουμε ένα τραπέζιο;» κ.λπ.
Δράση παιδιών: Τα παιδιά με τη σειρά τους επεξεργάζονται τις εικόνες που τους δείχνουμε αναγνωρίζοντας ορισμένα από τα σχήματα σε αυτές. Συμμετέχουν στην όλη διαδικασία κάνοντας διάλογο μαζί μας και αναγνωρίζοντας γεωμετρικά μοτίβα ακόμα και πάνω στα ρούχα που φοράνε. Κατά τη διάρκεια της δραστηριότητας στη γωνιά των μαθηματικών που περιλαμβάνει το γεωπίνακα, διατυπώνονται μερικές ερωτήσεις, όπως: «Αυτό που έφτιαξα είναι τρίγωνο;», «Γιατί δεν μπορώ να φτιάξω κύκλο;», «Πώς φτιάχνεται ένα τετράγωνο;»
Τα παιδιά με τη βοήθειά μας χρησιμοποιούν φελιζόλ για να φτιάξουν δύο νέους δικούς τους γεωπίνακες. Τοποθετώντας τα καρφάκια σε συγκεκριμένα σημεία και μετακινώντας τα δημιουργούν διάφορα γεωμετρικά σχήματα, χωρίς όμως και εδώ να λείπουν οι ερωτήσεις: «πόσα καρφάκια να βάλω για να φτιάξω ένα τετράπλευρο;», «αν βάλω έτσι τα καρφάκια θα είναι σκαληνό το τρίγωνο;», «πόσο μακριά να βάλω αυτό το καρφάκι;» κ.λπ.
Τα υλικά που χρησιμοποιήσαμε για τη διεξαγωγή αυτής της δραστηριότητας ήταν: Εικόνες υφασμάτων και ρούχων πάνω στα οποία απεικονίζονται γεωμετρικά μοτίβα και σχήματα εκτυπωμένες ή από Η/Υ, αυτοσχέδιοι γεωπίνακες, πολύχρωμα λαστιχάκια, φελιζόλ.

Με τη βοήθεια του γεωπίνακα έχουμε τη δυνατότητα να καταλάβουμε κατά πόσο τα παιδιά έχουν κατανοήσει τη μορφή και τα χαρακτηριστικά των γεωμετρικών σχημάτων αλλά και το διαχωρισμό ανάμεσά τους.Στη συνέχεια με τη δημιουργία του δικού μας γεωπίνακα καταλαβαίνουν καλύτερα τη χρήση του και τον τρόπο με τον οποίο μπορούμε να φτιάξουμε τα δικά μας σχήματα όπως εμείς επιθυμούμε.
Δραστηριότητα 4η: Μουσική
Στόχοι: Δημιουργία μουσικού μοτίβου με βάση τα γεωμετρικά σχήματα. Ταχεία αναγνώριση των διαφορετικών γεωμετρικών σχημάτων μέσω μοτίβου. Συγχρονισμός κίνησης & σκέψης. .Αντιστοίχιση σχημάτων με την κατάλληλη ορολογία
Στην παρακάτω δραστηριότητα θα ασχοληθούμε με τη δημιουργία ενός μικρού μουσικού μοτίβου, το οποίο θα φτιάξουμε με μια σειρά από τα σχήματα που συναντήσαμε στις προηγούμενες δραστηριότητες. Μαζεύουμε τα παιδιά στη γωνιά της παρεούλας και τους λέμε ότι οι φίλοι μας από τη σχηματοχώρα έχουν ο καθένας από έναν αγαπημένο ήχο. Πιο συγκεκριμένα ο ήχος της κάθε ομάδας σχημάτων έχει να κάνει με τα χαρακτηριστικά της, ο ήχος των τριγώνων είναι το χτύπημα των δαχτύλων μας γιατί χρησιμοποιούμε τα τρία μας δάχτυλα για να τον παράγουμε, ο ήχος από τα τετράπλευρα είναι το παλαμάκι γιατί δημιουργούμε με τα χέρια μας τέσσερις φανταστικές πλευρές, ενώ ο ήχος από τα κυκλοειδή είναι η φωνή που βγάζουμε όταν λέμε «ΧΟ-ΧΟ», επειδή δημιουργούμε με το στόμα μας έναν κύκλο.Έχουμε ετοιμάσει ήδη έναν πίνακα που αναπαριστά τον ήχο με τον οποίο συνδέεται η κάθε ομάδα σχημάτων, και τον τοιχοκολλάμε στη γωνιά της παρεούλας. Στη συνέχεια επεξεργαζόμαστε με τα παιδιά το μουσικό μοτίβο που έχουμε ετοιμάσει, για παράδειγμα: Τετράπλευρο -> παλαμάκι, Τρίγωνο -> χτύπημα δαχτύλων, Τρίγωνο -> χτύπημα δαχτύλων, Κυκλοειδές -> «ΧΟ-ΧΟ», Τρίγωνο -> χτύπημα δαχτύλων, Τετράπλευρο -> παλαμάκι, Τετράπλευρο -> παλαμάκι, Τρίγωνο -> χτύπημα δαχτύλων, Τρίγωνο -> χτύπημα δαχτύλων, Κυκλοειδές -> «ΧΟ-ΧΟ», Τετράπλευρο -> παλαμάκι, Τρίγωνο -> χτύπημα δαχτύλων, Τετράπλευρο -> παλαμάκι, Κυκλοειδές -> «ΧΟ-ΧΟ», Τετράπλευρο -> παλαμάκι, Τετράπλευρο -> παλαμάκι, Τρίγωνο -> χτύπημα δαχτύλων, Τρίγωνο -> χτύπημα δαχτύλων, Κυκλοειδές -> «ΧΟ-ΧΟ», Τρίγωνο -> χτύπημα δαχτύλων.
Αφού αρχικά ξεχωρίσουμε και πούμε σε ποια κατηγορία σχημάτων ανήκει το καθένα, καθώς και πως ονομάζεται η υποκατηγορία αυτή, το μουσικό μοτίβο που θα παράγουμε θα επαναληφθεί όσες φορές χρειαστεί για να γίνει κατανοητό από τα παιδιά. Ενώ στη συνέχεια μπορούμε να προτείνουμε όποιος θέλει να δημιουργήσει το δικό του μουσικό μοτίβο και οι υπόλοιποι να το εκτελέσουμε, δίνοντας με αυτόν τον τρόπο την ευκαιρία στα παιδιά να διαμορφώσουν μόνα τους ένα μέρος της δραστηριότητας και να γίνουν συνδημιουργοί. Σκοπός της δραστηριότητας αυτής είναι τα παιδιά να αναγνωρίζουν με ευκολία τις διαφορετικές ομάδες των σχημάτων, καθώς πλέον τα σχήματα μετατρέπονται σε σύμβολα που τα μεταφράζουμε σε έναν συγκεκριμένο ήχο. Τα παιδιά πλέον καλούνται να αναγνωρίσουν με ταχύτητα τις διαφορές των ομάδων που έχουν επεξεργαστεί στις προηγούμενες δραστηριότητες καθώς και τις διαφορές που υπάρχουν στο ίδιο σχήμα, όπως για παράδειγμα στα τετράπλευρα το τετράγωνο, ο ρόμβος, το τραπέζιο, το ορθογώνιο παραλληλόγραμμο, στα τρίγωνα το ισοσκελές, το σκαληνό , και στο κύκλο άλλες μορφές όπως η έλλειψη. Σημαντικό ακόμη είναι το γεγονός ότι τα παιδιά πειραματίζονται με την ανακάλυψη ενός νέου κανόνα, αυτού της ακολουθίας των σχημάτων με σκοπό τη δημιουργία ενός δεδομένου μουσικού μοτίβου το οποίο και αναπαράγουν όσες φορές θελήσουν. Καταφέρνουν λοιπόν να ξεχωρίσουν και να αντιστοιχίσουν κάθε σχήμα με έναν ήχο μέσα από μια διαδικασία δημιουργική και διασκεδαστική. Με το τέλος της δραστηριότητας αυτής δημιουργούμε ένα νέο χάρτη εννοιών, αντίστοιχο με τον αρχικό, τον οποίο τον συμπληρώνουν τα παιδιά με όσα στοιχεία κράτησαν από τις δραστηριότητες που προηγήθηκαν, καθώς και με λεπτομέρειες που αυτά θεωρούν σημαντικές και αξιόλογες. Ο νέος αυτός πίνακας των γνώσεων της τάξης μας για τα γεωμετρικά σχήματα τοιχοκολλάται δίπλα στον αρχικό και ακολουθεί συζήτηση με τα παιδιά συγκρίνοντας τις αρχικές μας γνώσεις για τα σχήματα με όσα γνωρίζουμε κατόπιν των όσων κάναμε.
Δράση εκπαιδευτικού: Αρχικά η ερωτήσεις για το ποιοι θα μπορούσαν να είναι οι αγαπημένοι ήχοι των σχημάτων. « Η κάθε οικογένεια σχημάτων που γνωρίσαμε χθες έχει τον αγαπημένο της ήχο, ποιος νομίζετε είναι ο αγαπημένος ήχος των τριγώνων; Είναι το χτύπημα των δαχτύλων μας! Μπορεί κάποιος να σκεφτεί γιατί; Θυμάστε που μας είπε η Τριγωνούλα ότι έχει τρεις πλευρές και τρεις γωνίες; Γι’ αυτό λοιπόν, γιατί χρησιμοποιούμε τρία δαχτυλάκια για να κάνουμε αυτόν τον ήχο. Ο αγαπημένος ήχος από την οικογένεια των τετραπλεύρων ποιος νομίζετε πως είναι; Είναι τα παλαμάκια! Γιατί χτυπώντας παλαμάκια σχηματίζουμε με τα δυο μας τα χεράκια ένα λεπτό τετράπλευρο! Το βλέπετε όλοι; Και τελευταία τα κυκλοειδή… ποιος να είναι άραγε ο αγαπημένος ήχος των φίλων μας των κύκλων; Βγαίνει από το στόμα όταν φωνάζουμε «ΧΟ-ΧΟ», φαντάζεστε γιατί; Για κοιτάξτε το στόμα μου όταν φωνάζω «ΧΟ-ΧΟ», τι σχηματίζει; Έναν μικρό κύκλο!». Στη συνέχεια λέμε στα παιδιά να δοκιμάσουμε να κάνουμε όλοι μαζί τους ήχους από τα σχήματα, και τους παρουσιάζουμε τον πίνακα πάνω στον οποίο απεικονίζεται η αντιστοιχία του κάθε ήχου με την ομάδα των σχημάτων. Με τον ίδιο τρόπο παρουσιάζουμε στα παιδιά το χαρτόνι με το ήδη σχηματισμένο μουσικό μοτίβο, και τους ζητάμε να αναγνωρίσουν τα σχήματα που απεικονίζονται σε αυτόν και να τα ονομάσουν με τη μαθηματική τους ορολογία που ήδη έχουν μάθει. « Πρώτο ποιο σχήμα είναι στη σειρά; Δηλαδή ποιο τετράπλευρο ακριβώς είναι; Μετά ποιο ακολουθεί;… είσαι σίγουρος ότι αυτό είναι οβάλ;…» κ.ο.κ. Τέλος προτείνουμε όποιος θέλει να σηκωθεί και να μπερδέψει τη σειρά των σχημάτων. «Ποιος θέλει να μας ανακατώσει λιγουλάκι; Να έχουμε μια καινούργια μουσική!...» Κατά τον αναστοχασμό έχουμε απλά προτρεπτικό ρόλο να μας πουν και στη συνέχεια να περάσουν τα νήπια τις γνώσεις που απέκτησαν στο νέο πίνακα.
Δράσεις Παιδιών: Αρχικά τα παιδιά υποθέτουν τον αγαπημένο ήχο της κάθε ομάδας σχημάτων, «μήπως ο αγαπημένος ήχος του τετραπλεύρου είναι το χτύπημα των ποδιών μας στο πάτωμα;», και συμμετέχουν με τις ιδέες τους στην παρουσίαση που κάνει η εκπαιδευτικός για τους ήχους που θα χρησιμοποιήσουμε.
Συνεχίζοντας τα παιδιά προσπαθούν να αναγνωρίσουν τα διάφορα σχήματα πάνω στο πίνακα με το μουσικό μοτίβο, «αφού αυτό δεν είναι ίσιο γιατί είναι τετράπλευρο;», « αυτό το περίεργο τρίγωνο πώς είπαμε πως λέγεται;» «δες εδώ έχει τα ίδια σχήματα όπως και πιο κάτω!» κ.ο.κ. Κατά τη διάρκεια της δραστηριότητας καλούνται να παράγουν ήχους χρησιμοποιώντας τα μέλη του σώματός, αλλά και να αναδημιουργήσουν το μουσικό μοτίβο.
Τα υλικά που χρησιμοποιούνται για την παραπάνω δραστηριότητα είναι: Χαρτόνια, Μαρκαδόροι, Διάφορα γεωμετρικά σχήματα, Πίνακας σε κανσόν χαρτόνι με την αντιστοιχία σχημάτων και ήχων, Πίνακας σε κανσόν χαρτόνι για το μουσικό μοτίβο με πλαστικές θήκες.


Με την τελική αυτή δραστηριότητα τα παιδιά καταφέρνουν πλέον με ταχύτητα να αναγνωρίζουν τα γεωμετρικά σχήματα, να ξεχωρίζουν τις επιμέρους διαφορές τους, με αποτέλεσμα να παράγουν σωστά μουσικά μοτίβα. Είναι το τελευταίο στάδιο με το οποίο καταλαβαίνουμε αν τα παιδιά έχουν κατακτήσει επαρκώς τα χαρακτηριστικά των σχημάτων και την ορολογία τους. Προφανώς δεν είναι εφικτή η δημιουργία του μουσικού μοτίβου από την πρώτη προσπάθεια, αλλά με υπομονή και συνεχείς επαναλήψεις μπορούμε να έχουμε ένα εύηχο μουσικό μοτίβο.
Αργυρόπουλος, Η., Βλάμος, Π., Κατσούλης, Γ. & Μαρκάτης, Σ. (2001). Ευκλείδια γεωμετρία Α’ και Β’ ενιαίου Λυκείου. Αθήνα: Οργανισμός Εκδόσεων Διδακτικών Βιβλίων
Θεοχάρη Περάκη, Ε. (1994). Κουκλοθέατρο. Τέχνη και Τεχνική. Αθήνα: Εστία
Κανίστρα, Μ. (1991). Η σύγχρονη εικαστική αγωγή στο σχολείο. Αθήνα: Εκδόσεις Σμιλή
Τσαφταρίδης, N. (1997). Mουσική, κίνηση, λόγος. H στοιχειοδομική μουσική στο παιδαγωγικό έργο του Orff. Αθήνα: Εκδόσεις Νήσος
Van de Walle, J. A. (2007). Διδάσκοντας Μαθηματικά για Δημοτικό και Γυμνάσιο. Μια αναπτυξιακή διαδικασία. Αθήνα: Εκδόσεις Επίκεντρο
http://maths-art.blogspot.com/ (2011)
http://www.viokliron.gr/documents/Yfantiki_texni.pdf (2011)