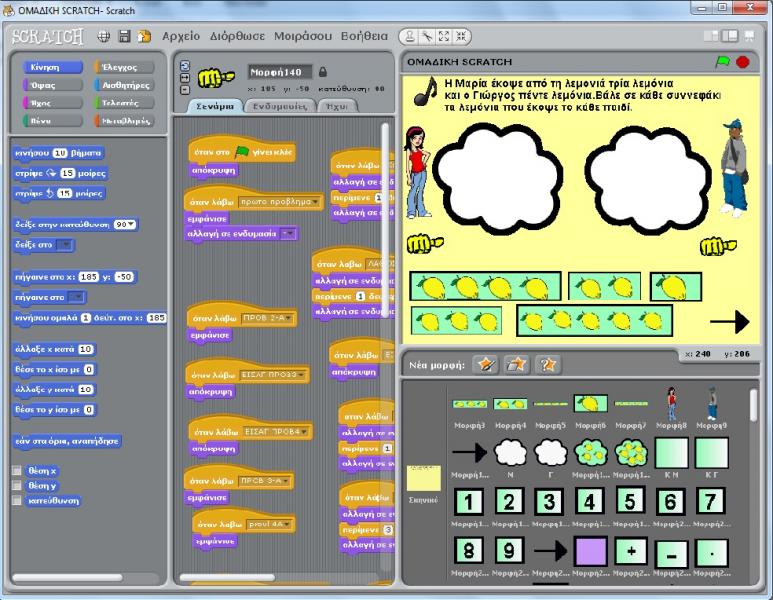
Τα προβλήματα που δημιουργήθηκαν γι’ αυτή την εργασία είναι ατομικά που σημαίνει ότι κάθε παιδί δουλεύει μόνο του σε διαφορετικό υπολογιστή, εάν αυτό δεν είναι εφικτό τα παιδιά μπορούν να δουλέψουν σε ομάδες των δύο ατόμων. Το καθένα απ’ αυτά τα πρόβλημα απαρτίζεται από τέσσερα επίπεδα. Τα επίπεδα αυτά είναι διαβαθμισμένης δυσκολίας και σε κάθε επίπεδο διαφοροποιούνται τα δεδομένα και τα ζητούμενα.
Αναλυτικότερα:
1^ο επίπεδο: Στο επίπεδο αυτό δίνεται στα παιδιά μια ιστορία. Για την κατασκευή αυτής της ιστορίας χρησιμοποιήσαμε αντικείμενα οικεία στα παιδιά που έρχονται σε επαφή μαζί τους στην καθημερινότητα και οι πρωταγωνιστές είναι μικρά παιδιά, για να είναι εύκολο να ταυτίζονται τα νήπια με τις μορφές των ιστοριών. Μέσω της ιστορίας παρουσιάζονται σ’ αυτά τα δεδομένα και τα ζητούμενα που καλούνται να αναγνωρίσουν. Εφόσον τα παιδιά επεξεργαστούν τις πληροφορίες του προβλήματος καλούνται να αριθμήσουν τα αντικείμενα. Με αυτό τον τρόπο ενθαρρύνονται τα παιδιά να αριθμούν και να απαριθμούν για να εξοικειωθούν με τα ονόματα και με τη σειρά ακολουθίας των φυσικών αριθμών και να συνειδητοποιήσουν προοδευτικά ότι το καθετί αριθμείται μία μόνο φορά, ότι ο τελευταίος αριθμός στη σειρά αρίθμησης αναφέρεται στο πλήθος των αντικειμένων μια συλλογής. Τέλος, σ’ αυτό το επίπεδο των προβλημάτων τα παιδιά μετά την απαρίθμηση των αντικειμένων καλούνται να αντιστοιχίσουν το σωστό πλήθος με την ανάλογη μορφή.
2^ο επίπεδο: Αφού τα νήπια έχουν ολοκληρώσει με επιτυχία το 1^ο επίπεδο στο 2^ο επίπεδο τους δίνεται πάλι η ίδια ιστορία (ίδιοι πρωταγωνιστές, ίδια αντικείμενα) μόνο που στη φάση αυτή διαφοροποιούνται τα ζητούμενα. Συγκεκριμένα, τους δίνεται ένα πλήθος αριθμών από το 1-10 και τα παιδιά καλούνται να επιλέξουν το σωστό αριθμό για το πλήθος των αντικειμένων που έχει ο κάθε ήρωας της ιστορίας.
3^ο επίπεδο: Στο επίπεδο αυτό εισάγεται στα παιδιά ένα διαφορετικό ζητούμενο. Ενώ μέχρι τώρα αυτό που έπρεπε να κάνουν ήταν να αναγνωρίσουν και να απαριθμήσουν αντικείμενα, τώρα καλούνται να αναγνωρίσουν το κατάλληλο σύμβολο που αντιπροσωπεύει την αντίστοιχη πράξη μέσα στο πρόβλημα. Εκτός όμως από την αναγνώριση των συμβόλων, σημαντικό ρόλο παίζει και η κατανόηση της χρησιμότητας του κάθε συμβόλου, δηλαδή της πρόσθεσης και της αφαίρεσης αριθμών. Μ’ αυτό τον τρόπο τα παιδιά αντιλαμβάνονται ότι πρόκειται για δύο διαφορετικές πράξεις, να εξοικειωθούν μ’ αυτές και να συνειδητοποιήσουν ότι η πρόσθεση κατονομάζει το όλο σε σχέση με τα μέρη και η αφαίρεση χρησιμοποιείται όταν είναι γνωστά το όλο κι ένα από τα μέρη και κατονομάζει το άλλο μέρος.
4^ο επίπεδο: Το επίπεδο αυτό αποτελεί το τελευταίο επίπεδο στη διαδικασία ανάλυσης προβλημάτων. Εδώ τα παιδιά έχοντας κατανοήσει την έννοια της αρίθμησης, της αναγνώρισης των αριθμών και των δυο βασικών πράξεων της πρόσθεσης και της αφαίρεσης καλούνται να συνδυάσουν όλα αυτά προκειμένου να φτάσουν στο αποτέλεσμα αυτής της πράξης, το οποίο είναι και το ζητούμενο στο επίπεδο αυτό. Δεδομένου ότι η διατύπωση και ο έλεγχος υποθέσεων αποτελούν βασικά χαρακτηριστικά της μαθηματικής σκέψης, στη φάση αυτή τα παιδιά ενθαρρύνονται να επεξεργάζονται τα μέχρι τώρα δεδομένα να κάνουν υποθέσεις αλλά και να ελέγχουν τις συνέπειες της υπόθεσής τους σε σχέση με το πρόβλημα που έχουν να αντιμετωπίσουν.
Τα παιδιά μέσα από την ενασχόλησή τους με τη συγκεκριμένη μαθησιακή δραστηριότητα έρχονται σε επαφή με τις μαθηματικές έννοιες, διαμορφώνουν ένα τρόπο μαθηματικής σκέψης. Τέλος, ενθαρρύνονται να κάνουν εκτιμήσεις, να επεξεργάζονται και να απαριθμούν τα δεδομένα που τους δίνονται για να καταλήξουν στο αποτέλεσμα, να αιτιολογούν τις επιλογές τους. Είναι σε θέση να κάνουν σύγκριση περιπτώσεων, να διαχειρίζονται τα λάθη τους και να αιτιολογούν βασικές ερωτήσεις και γενικά η ενασχόλησή τους αυτή συμβάλει στην ανάπτυξη της κριτικής σκέψης. Ο ρόλος του εκπαιδευτικού εδώ είναι απλά ενθαρρυντικός και καθοδηγητικός (εμψύχωση παιδιών, διατύπωση ερωτημάτων για την κατανόηση του τρόπου σκέψης τους). «Ζητά από τους μαθητές να εξηγήσουν τον τρόπο με τον οποίο υπολόγισαν το αποτέλεσμα. Το να εξηγεί ο μαθητής τον τρόπο με τον οποίο υπολογίζει είναι μια πολύ χρήσιμη διανοητική ενέργεια (μεταγνωστική διαδικασία). Επίσης, ο δάσκαλος δίνει τη δυνατότητα να εκφραστούν, να συζητηθούν και να καταγραφούν όλοι οι δυνατοί τρόποι υπολογισμού μιας πράξης.»
Αναστοχασμός: Αν είχαμε την ευκαιρία να σχεδιάσουμε από την αρχή την συγκεκριμένη εργασία με θέμα την ανάλυση λεκτικών προβλημάτων τα πράγματα που θα διαφοροποιούσαμε είναι τα ακόλουθα: (α) Εμπλουτισμός της δραστηριότητας με περισσότερα προβλήματα. Λόγω έλλειψης χρόνου δεν υπήρχε η δυνατότητα να βάλουμε περισσότερα προβλήματα. Γι’ αυτό θα ήταν ένα από τα πρώτα σημεία που θ’ αλλάζαμε. Θα μπορούσαμε να εμπλουτίσουμε την δραστηριότητα με περισσότερα προβλήματα διαβαθμισμένης δυσκολίας. Να ξεκινάμε από απλά προβλήματα με λίγα δεδομένα και συνεχίζοντας να γίνονται δυσκολότερα με περισσότερα δεδομένα. (β) Εμπλουτισμός των προβλημάτων με περισσότερα επίπεδα. Για την ανάλυση των λεκτικών προβλημάτων και για να φτάσουμε στο αποτέλεσμα θα μπορούσαν να χρησιμοποιηθούν περισσότερα επίπεδα στο κάθε πρόβλημα. Με τον τρόπο αυτό τα παιδιά θα μπορούσαν να κατανοήσουν σε μεγαλύτερο βαθμό τα προβλήματα, να επεξεργαστούν καλύτερα τα δεδομένα και να καταλήξουν στο αποτέλεσμα με μεγαλύτερη ακρίβεια. (γ) Μεγαλύτερη κλίμακα αριθμών (1-20). Το τρίτο και τελευταίο σημείο που θα τροποποιούσαμε θα ήταν η κλίμα των αριθμών. Όπως προαναφέρθηκε τα προβλήματα θα ήταν διαβαθμισμένης δυσκολίας που αυτό συνεπάγεται πως και η κλίμακα των αριθμών θα ήταν διαφορετική. Συγκεκριμένα, στα προβλήματα εύκολου επιπέδου δυσκολίας θα χρησιμοποιούσαμε αριθμούς από το 0-10, στα μέτριας δυσκολίας 0-20 και στα δύσκολα προβλήματα αριθμούς 0-30.

Οι στόχοι της συγκεκριμένης μαθησιακής δραστηριότητας είναι η επίλυση προβλημάτων, η χρήση σύγχρονης τεχνολογίας για την επίλυση μαθηματικών προβλημάτων, η αρίθμηση, η αναγνώριση και η πρόσθεση και αφαίρεση αριθμών από το 1-10, η διάκριση και αναγνώριση συμβόλων πράξεων, η συνειδητοποίηση της αναγκαιότητας των συμβόλων και των μαθηματικών πράξεων στην καθημερινότητα, η διατύπωση και έλεγχος υποθέσεων και αποτελεσμάτων, η επεξεργασία δεδομένων και να κάνουν εκτιμήσεις. Αναλυτικότερα:
Επίλυση προβλημάτων: «Τα προβλήματα είναι καταστάσεις τις οποίες το παιδί καλείται να λάβει αποφάσεις για το πώς θα επεξεργαστεί κάποιες πληροφορίες ποσοτικού ή ποιοτικού χαρακτήρα, ώστε να οδηγηθεί σε κάποιο αποτέλεσμα, το οποίο στη συνέχεια θα ελέγξει για την ορθότητα του. Η επίλυση προβλημάτων τίθεται πλέον ως κύριος στόχος της μαθηματικής εκπαίδευσης σήμερα. Στο πλαίσιο του καθημερινού προγράμματος στο νηπιαγωγείο, όπως ήδη αναφέρθηκε, δίνονται πολλές ευκαιρίες για επίλυση προβλημάτων, με αξιοποίηση των γνώσεων που έχουν ήδη κατακτήσει τα παιδιά εντός ή εκτός σχολικού πλαισίου.»(1)
Χρήση σύγχρονης τεχνολογίας για την επίλυση μαθηματικών προβλημάτων: Στην εποχή μας η ανάπτυξη της τεχνολογίας είναι ραγδαία, αυτό έχει ως αποτέλεσμα ακόμα και στο νηπιαγωγείο, τα παιδιά να έρχονται σε επαφή με τους υπολογιστές και άλλα μέσα της σύγχρονης τεχνολογίας. Αυτό βοηθάει τα παιδιά να συνδέσουν την μάθηση που πραγματοποιείται στο σχολείο με τις μαθηματικές εμπειρίες που έχουν βιώσει στην καθημερινότητα τους. Η χρήση των τεχνολογικών αυτών μέσων διεγείρει την περιέργειά τους, προσελκύει το ενδιαφέρον τους με αποτέλεσμα η μάθηση να αποκτά διασκεδαστικό χαρακτήρα.
Αρίθμηση και αναγνώριση αριθμών από το 1-10: Τα παιδιά ενθαρρύνονται να αριθμούν και να απαριθμούν για να εξοικειωθούν με τα ονόματα και με τη σειρά ακολουθίας των φυσικών αριθμών και να συνειδητοποιήσουν ότι το καθετί αριθμείται μόνο μία φορά και ότι ο τελευταίος αριθμός στη σειρά αρίθμησης αναφέρεται στο πλήθος των αντικειμένων μίας συλλογής.
Πρόσθεση και αφαίρεση αριθμών από το 1-10: Να κατανοήσουν ότι πρόκειται για δύο διαφορετικές πράξεις, να εξοικειωθούν μ’ αυτές και να συνειδητοποιήσουν ότι η πρόσθεση κατονομάζει το όλο σε σχέση με τα μέρη και η αφαίρεση χρησιμοποιείται όταν είναι γνωστά το όλο κι ένα από τα μέρη και κατονομάζει το άλλο μέρος.
Διάκριση και αναγνώριση συμβόλων πράξεων: Να αναγνωρίζουν ποιο σύμβολο αντιστοιχεί σε κάθε πράξη (πρόσθεση, αφαίρεση κλπ) αλλά και τη σημασία και τη χρησιμότητα του καθενός.
Να συνειδητοποιήσουν την αναγκαιότητα των μαθηματικών πράξεων στην καθημερινότητα: Η χρήση των μαθηματικών πράξεων επιτρέπει στα παιδιά να αναπτύξουν ικανότητες και δεξιότητες που θα τα βοηθήσουν στην μετέπειτα ζωή τους και να συνειδητοποιήσουν πως οι πράξεις αυτές είναι απαραίτητες καθώς στην καθημερινή τους ζωή θα έρχονται συνεχώς αντιμέτωπα μ’ αυτές.
Να κάνουν εκτιμήσεις: «Ενθαρρύνοντας τα παιδιά να κάνουν εκτιμήσεις επιδιώκουμε να τα βοηθήσουμε να συνειδητοποιήσουν την αξία των εκτιμήσεων και όχι να πάρουμε απαραίτητα τη σωστή απάντηση.»(1)
Διατύπωση και έλεγχος υποθέσεων και αποτελεσμάτων: «Η διατύπωση και ο έλεγχος υποθέσεων αποτελούν βασικά χαρακτηριστικά της μαθηματικής σκέψης. Τα παιδιά ενθαρρύνονται να σκέφτονται τι θα μπορούσε να συμβεί σε υποθετικές περιπτώσεις, αλλά και να ελέγχουν τις συνέπειες της υπόθεσής τους σε σχέση με το πρόβλημα που συζητιέται κάθε φορά.»(2)