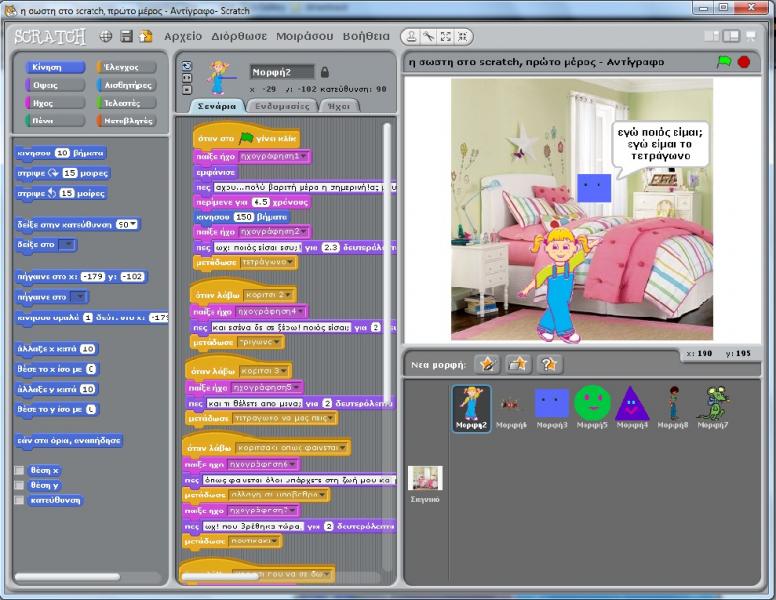
Το Scratch αποτελεί ένα καλοσχεδιασμένο σύγχρονο ανοιχτό προγραμματιστικό πολυμεσικό Logo-like περιβάλλον, το οποίο επιτρέπει στον χρήστη να δημιουργήσει εύκολα μοντελοποιήσεις, προσομοιώσεις, διαδραστικές ιστορίες, κινούμενα σχέδια κ.ά. Στην προκειμένη περίπτωση, στο πλαίσιο μιας ιστορίας, τα παιδιά γνωρίζουν ένα- ένα τρια γεωμετρικά σχήματα(τρίγωνο, τετράγωνο, κύκλο), τις ιδιότητές τους και τη συσχέτιση με την καθημερινότητα τους. Επιπρόσθετα, έρχονται σε επαφή με την μαθηματική έννοια του μεγέθους μέσα απο μια διαδικασία συγκρίσεων. Το περιβάλλον περιέχει μορφές, ήχους, σενάρια, ηχογραφήσεις και εναλλαγή σκηνικού. Μέσω της εικονικής ηρωίδας, τίθενται προβληματισμοί οι οποίοι οδηγούν σε λογικά συμπεράσματα.

Στη συνέχεια κρίνεται αναγκαίο τα ίδια τα παιδιά να πειραματιστούν με την κατασκευή, τη και τη σύγκριση των γεωμετρικών σχημάτων. Καταλληλότερο πρόγραμμα για τη χρήση αυτή, εκτιμήθηκε πως είναι το geogebra(λογισμικό για τη διδασκαλία άλγεβρας, μαθηματικών και γεωμετρίας σε όλες τις βαθμίδες της εκπαίδευσης) και έτσι τα παιδιά παραπέπονται στο εν λόγω λογισμικό(βήμα 2ο). Στο βήμα αυτό τα παιδιά καλούνται μέσω ερωτημάτων, να θυμηθούν τα γεωμετρικά σχήματα, να διαπιστώσουν τις διαφορές ανάμεσα σε σχήματα που στο ψηφιακό περιβάλλον μένουν σταθερά και στα ομοειδή τους που μεταβάλλονται , να διατυπώσουν τις παρατηρήσεις, τις υποθέσεις και τις προβλέψεις τους, να δημιουργήσουν σχήματα(στο ψηφιακό περιβάλλον), να πειραματιστούν ελέυθερα, να εκφράσουν τις απορίες και να μοιραστούν τις σκέψεις τους.
Όταν ολοκληρώνεται και η παρούσα διαδικασία, είναι καλό, τα παιδιά να έρθουν σε επαφή με αντίστοιχο απτικό υλικό(βήμα 3ο). Το απτικό υλικό συγκεκριμένα, είναι «γεωπίνακες», μέσω των οποίων τα παιδιά με τη βοήθεια των λαστίχων μπορούν να δημιουργησουν ελεύθερα σχήματα σε διάφορα μεγέθη.
Η διαδικασία δεν σταματάει εδώ. Είναι σκόπιμο να γίνει ανατροφοδότηση της γνώσης και της εμειρίας που τα παιδιά οικομόδησαν(Βήμα 4ο). Έτσι, επανερχόμαστε στο ψηφιακό περιβάλλον του Scratch, και μέσω μιας διαδραστικής πορείας τα παιδιά απαντούν μόνα τους σε ερωτήματα που τίθενται από τους ήρωες. Σε περίπτωση λάνθασμένων απαντήσεων, το πρόγραμμα τους παρέχει τη δυνατότητα εντοπισμού του λάθους και διόρθωσής αυτού, απαντώντας εκ νέου.
Εάν κριθεί σκόπιμο, η μαθησιακές μας δραστηριότητες δεν σταματούν εδώ! Επιχειρείται η διδασκαλία του πολυγώνου. Και πάλι στο ψηφιακό περιβάλλον του scratch έχουμε ετοιμάσει ένα animation κατά το οποίο τα παιδιά γνωρίζουν διάφορα είδη πολυγώνων και τις ιδιότητές τους. Και αυτή τη φορά, οι γεωπίνακες θα χρησιμοποιηθούν για την εξάσκηση και την περαιτέρω τριβή με την εν λόγω μαθηματική έννοια.

Πρώτη Διδακτική Συνάντηση
Η Νηπιαγωγός συγκεντρώνει τα παιδιά στη γωνία της παρεούλας. Στα χέρια της κρατάει μια φέτα του τόστ, μια ρόδα αυτοκινήτου (μινιατούρας) και ένα τρίγωνο χριστουγέννων και θέτει τα εξής ερωτήματα: « παιδιά ολοι σας γνωρίζετε τι κρατάω στα χέρια μου. Έχετε σκεφτεί ποτέ τι σχήμα έχει το κάθε ένα από αυτά». Τα παιδιά εκφράζουν ελεύθερα τις ιδέες τους και έτσι η Νηπιαγωγός ανιχνεύει κάποιες από τις αρχικές αντιλήψεις τους. Στη συνέχεια ρωτάει « Έχω μια ιδέα! Θέλετε να παρακολουθήσουμε ένα πρόγραμμα στους υπολογιστές μας σχετικά με ένα κοριτσάκι που γνωρίζει πολλά και ενδιαφέροντα πράγματα;»
Στην οθόνη ενός κεντρικού υπολογιστή τα παιδιά ανοίγουν συνεργατικά τον υπολογιστή, και στη συνέχεια το πρόγραμμα scratch. Η Νηπιαγωγός τα προτρέπει να πατήσουν το πράσινο σημαιάκι, προκειμένου να αρχίσει η προβολή τουν προγράμματος με τίτλο «Μια περίεργη μέρα» που έχουμε δημιουργήσει. Όλοι μαζί παρακολουθούνε την ιστορία, έτσι όπως εξελίσσεται: Σε ένα ευχάριστο σκηνικό υπόβαθρο(παιδικό δωμάτιο), εμφανίζονται στην ηρωίδα μας, ένα μικρό κοριτσάκι , τρία γεωμετρικά σχήματα, ο κύκλος, το τρίγωνο και το τετράγωνο τα οποία αυτοσυστήνονται. Η ηρωίδα τους ρωτάει για το λόγο της εμφάνισής τους. Τα σχήματα την καλούν να αποφασίσει ποιος από αυτά είναι ο καλύτερος. Έτσι το κάθε σχήμα, εξαίρει τα προσόντα του αναφερόμενο στις χαρακτηριστικές του ιδιότητες(ο κύκλος δεν έχει γωνίες, το τρίγωνο έχει τρείς γωνίες και πλευρές, το τετράγωνο τέσσερεις γωνίες και πλευρές) και συσχετίζουν την ύπαρξή τους με την καθημερινότητα της ηρωίδας. Η ηρωίδα εξηγεί ότι καθώς όλα τα σχήματα είναι χρήσιμα, αφού υπάρχουν στη ζωή της, δεν μπορεί να διαλέξει το καλύτερο και μεταφέρεται σε ένα σκηνικό εξωτερικού χώρου. Στο σημείο αυτό, τη θέση των σχημάτων αντικαθιστούν σταδιακά διάφοροι ήρωες: ένα μικρό ποντικάκι, ένα μικρότερο κατσαριδάκι και ένα μαγαλύτερο σε μέγεθος αγόρι. Κάθε ήρωας διαπιστώνει ότι είναι μικρότερος ή μεγαλύτερος σε σχέση με κάποιον άλλον. Η ηρωίδα αντιλαμβάνεται ότι το μέγεθος της καθορίζεται από την σύγκρισή του με άλλα μεγέθη. Οι παρευρισκόμενοι ήρωες φεύγουν και το κορίτσι μεταφέρεται σε ένα όμορφο πάρκο, από το οποίο καλεί τα παιδιά να θυμηθούνε τα όσα πραγματώθηκαν μέσω του λογισμικού geogebra.
Με την υποστήριξη της Νηπιαγωγού, τα παιδιά ανοίγουν το πρόγραμμα geogebra και έρχονται σε επαφή με το πρώτο φύλλο εργασίας. Η Νηπιαγωγός χωρίζει τα παιδιά σε ομάδες,(ομαδοσυνεργατική μέθοδος)ανάλογα με τον αριθμό των υπολογιστών που υπάρχουν μέσα στην αίθουσα του νηπιαγωγείου, ώστε να υπάρχει αντιστοιχία. Φροντίζει προκειμένου όλα τα νήπια να κάνουν χρήση του υπολογιστή μέσα σε ένα ενθαρρυντικό και συνεργατικό περιβάλλον. Προβάλλονται τρία φύλλα,το κάθε ένα από τα οποία περιέχει δύο ομοειδή και φαινομενικά όμοια σχήματα(δύο κύκλοι, δύο τρίγωνα, δύο τετράγωνο). Το ένα σχήμα μένει σταθερό, ενώ το άλλο μπορεί εάν «πειραχθεί» να μεταβληθεί. Τα παιδιά καλούνται να πειραματιστούν με τα δύο σχήματα στο κάθε ένα φύλλο και να διαπιστώσουν τα αποτελέσματα, έτσι όπως θα προκύψουν από το «πείραγμα». Σε περίπτωση έλλειψης συνεργασίας από τη μεριά των παιδιών, η Νηπιαγωγός παρεμβαίνει, δίνοντας συγκεκριμένες οδηγίες σε κάθε μέλος της ομάδας, διαδοχικά.
Ανάλογα με την κούραση και τη διάθεση για ενασχόληση που έχουνε τα παιδιά, η διδακτική συνάντηση θα φτάσει στο τέλος της. Η Νηπιαγωγός συγκεντρώνει και πάλι τα παιδιά στην παρεούλα και τους λέει « Θυμάστε το κοριτσάκι της ιστορίας μας που συναντουσε διάφορα σχήματα στη ζωή του; Θέλετε και εσείς στο σπίτι σας να παρατήρησετε και να βρείτε τέτοια σχήματα; Εάν σας επιτρέπουν οι γονείς σας μπορείτε να τα φέρετε αύριο εδώ και να συγκρίνουμε τα μεγέθη τους. Αλλιώς μπορείτε απλά να μας τα πείτε!»

Δεύτερη Διδακτική Συνάντηση
Τα παιδιά και η Νηπιαγωγός συγκεντρώνουν τα αντικείμενα διαφορετικών σχημάτων που έφεραν από το σπίτι. Ακολουθεί κουβέντα, κατά την οποία η Νηπιαγωγός θέτει ενδειτικά τα παρακάτω ερωτήματα: « Κοιτάξτε αυτό το καπάκι ; Τι σχήμα έχει; Είναι μικρότερο σε σχέση με αυτό το κουμπί; Γιατί λες ότι αυτό το τουβάκι είναι τετράγωνο; Μπορείς να το εξηγήσεις με βάση τα χαρακτηριστικά του;»
Όταν ολοκληρωθεί η παραπάνω διαδικασία η Νηπιαγωγός εμφανίζει στα παιδιά γεωπίνακες και χρωματιστά λαστιχάκια, καλώντας τα να δημιουργήσουν ό,τι θέλουν. Εάν δεν υπάρχει αντιστοιχία γεωπινάκων-παιδιών, η Νηπιαγωγός χωρίζει τα παιδιά σε ομάδες και τα παρακινεί να πειραματίζονται διαδοχικά, εξελίσσοντας το καθένα το σχήμα του προηγούμενου με σκοπό μια ομαδική δημιουργία. Με βάση τα σχήματα που έχουν δημιουργηθεί τίθενται ερωτήματα όπως : «Κοιτάξτε αυτό το σπιτάκι! Από ποια σχήματα αποτελείται; Για κοιτάξτε αυτά τα δύο ίδια τρίγωνα! Άμα τα ενώσουμε θα συμβεί κάτι; ». Τα παιδιά διατυπώνουν ελεύθερα τις υποθέσεις και τις ιδέες τους. Σε περίπτωση που προκύψουν μέσα από τις δημιουργίες τους καινούργια σχήματα, όπως ο ρόμβος ή ένα πολύγωνο, η Νηπιαγωγός δράττει την ευκαιρία και επεκτείνει τη διδασκαλία της, χτίζοντας πάνω στη δομηθείσα γνώση τους.

Μόλις ολοκληρωθεί η παραπάνω διαδικάσία, η Νηπιαγωγός ρωτάει τα παιδιά « Θέλετε να παίξουμε ένα παιχνίδι στο scratch; Χθές στο σπίτι μου βρήκα κάτι πολύ ενιδαφέον». Καθώς το σύνηθες είναι ότι οι υπολογιστές δε θα αντιστοιχούν στον αριθμό των παιδιών, η Νηπιαγωγός παρακινεί ένα ένα τα παιδιά να κάθονται στους υπάρχοντες υπολογιστές(εξατομικευμένη μέθοδος) και να παίζουν το «παιχνίδι». Προκείται για ένα διαδραστικό παιχνίδι- πρόγραμμα κατά το οποίο εμφανίζονται ένα ένα τα γεωμετρικά σχήματα και προκαλούν το παιδί να απαντήσει σε ερωτήματα που του θέτουν, σχετικά με τις ιδιότητές και τα χαρακτηριστικά τους: «Πόσες είναι οι γωνίες μου; Πόσες πλευρές μου;». Τα παιδιά απαντούν πληκτρολογώντας αριθμούς. Σε ενδεχόμενο λάθους απάντησης, το πρόγραμμα τους παρέχει τη δυνατότητα εντοπισμού του λάθους και διόρθωσής αυτού, απαντώντας εκ νέου. Η Νηπιαγωγός προσπαθεί να ι βρίσκεται κοντά και διακριτικά κατά τη διάρκεια της διάδρασης αυτής, προωθώντας την αυτονομία των παιδιών και αποφεύγοντας την περαιτέρω παρέμβαση. Η παρούσα φάση, είναι ένα άριστο υλικό προς αξιολόγηση, αφού η Νηπιαγωγός μπορεί να εντοπίσει κατά πόσο τα παιδιά οικοδόμησαν τη γνώση των εννοιών που αναπτύχθηκαν κατά τα προηγούμενα βήματα. Ταυτόχρονα, αφού το παιδί είναι μόνο του και δεν έχει την παρουσία ενός άλλου ανθρώπου, δε νιώθει ότι κρίνεται, μπορεί να πειραματίζεται και παράλληλα να οικοδομεί τις γνώσεις του.
Τρίτη Διδακτική Συνάντηση
Η συνέχεια των συναντήσεων είναι σκόπιμο να πραγματοποιηθεί εάν και εφόσον η Νηπιαγωγός, μέσω της αξιολόγησης, κρίνει ότι οι μέχρι τώρα έννοιες έχουνε γίνει αντιληπτές από τα παιδιά. Και πάλι το ψηφιακό περιβάλλον που επιλέγεται είναι το scratch και η έννοια που θα διαπραγματευτούμε είναι το «πολύγωνο».
Η Νηπιαγωγός δείχνει στα παιδιά ένα αντικείμενο πολύγωνικού σχήματος, π.χ. έναν χαρταετό και ρωτάει «Για πείτε μου παιδιά αυτό είναι κύκλος, τρίγωνο ή τετράγωνο….ή μήπως κάτι άλλο!;». Τα παιδιά εκφράζουν ελεύθερα τις ιδέες τους και η Νηπιαγωγός τους λέει: « Μήπως να δούμε μια ακόμη ιστορία στο scratch και να αποφασίσουμε μετά για να είμαστε σίγουροι;».
Παιδιά και Νηπιαγωγός παρακολουθούν ένα νέο animation στο εν λόγω πρόγραμμα, κατά το οποίο το πολύγωνο διαφοροποιεί την «προσωπικότητά του» από το τετράγωνο, προσδιορίζει τις ιδιότητές του και συστήνει τα «αδέλφια» του, δηλ. διαφορετικών ειδών πολύγωνα. Εάν τα παιδιά το επιθυμούν, ξαναπαίζουν το animation, και η Νηπιαγωγός ρωτάει τα παιδιά «Τελικά τι σχήμα λέτε να έχει ο χαρταετός μας;». Στο σημείο αυτό και πάλι η δημιουργία είναι απαραίτητο συστατικό για την κατάκτηση των εννοιών που αναπτύχθηκαν. Η Νηπιαγωγός φέρνει στα παιδιά τους γεωπίνακες και τα παρακινεί να κατασκευάσουν πολύγωνα. Και πάλι η Νηπιαγωγός ρωτάει τα παιδιά «τι σε κάνει να πιστεύεις ότι αυτό που έφτιαξες είναι πολύγωνο; Μπορείς να μου το εξηγήσεις;». Κατά το τέλος αυτής της διαδικασίας η Νηπιαγωγός ζητάει τα παιδιά, από κοινού, να κατασκευάσουν ένα σπιτάκι. Όταν δημιουργηθεί τίθενται ερωτήσεις όπως « Τι σχήμα έχει η στέγη; Τα παράθυρα; Όλο τα σπιτάκι μας μαζί πόσες γωνίες έχει; Άρα τι σχήμα είναι;». Τα παιδιά καταθέτουν τις σκέψεις τους και η Νηπιαγωγός τους παρέχει το χρόνο και τη δυνατότητας να πειραματιστούν όπως θέλουν και για όσο θέλουν.

Αναστοχασμός: Θεωρούμε ότι δραστηριότητα είναι προσεκτικά σχεδιασμένη, έτσι ώστε να μην κρύβει γνωστικά κενά ή αντιεκπαιδευτικές μεθόδους. Εντούτοις, η δραστηριότητα ενδεχομένως να «κλονιστεί» από τεχνικές δυσκολίες όπως π.χ. έλλειψη υπολογιστών, γεωπινάκων κτλ. Εάν σχεδιάζαμε εκ νέου τη δραστηριότητα, θα μπορούσαμε να παραμερίσουμε την έννοια του μεγέθους και να επεκτεινόμασταν σε περισσότερα γεωμετρικά σχήματα . Αντίστροφα, θα αναπτύσσαμε περεταίρω την έννοια του μεγέθους συγκρίνοντας διαφορετικά αντικείμενα και θα διαχωρίζαμε τον ηλικιακό όρο «μεγάλος-μικρός»από τη μαθηματική έννοια του μεγέθους. Ταυτόχρονα, θα διευρύναμε τη σύγκριση και σε άλλες μαθηματικές έννοιες όπως π.χ. σύγκριση ποσότητας(περισσότερο-λιγότερο).

Ακόμη, τα παιδιά θα μπορούσαν να χρησιμοποιήσουν τα σώματά τους για να αναπαραστήσουν κάποια σχήματα, ενδεχομένως με τη βοήθεια κορδέλων.Επιπρόσθετα, τα παιδιά, θα μπορούσαν να κάνουν μια εικαστική σύνθεση, χρησιμοποιώντας διαφορετικά σχήματα και μέσω αυτής της διαδικασίας να γινόταν η αναφορά σε επιπλέον γεωμετρικά σχήματα. Η αφόρμηση για μια τέτοια δημιουργία θα μπορούσε να είναι ένας καλλιτεχνικός πίνακας ή τα αντικείμενα από την καθημερινότητά των παιδιών.
Τέλος, στην εργασία μας θα μπορούσαμε να κάνουμε χρήση του προγράμματος kidspiration και μέσα από το εργαλείο picture view να δημιουργήσουμε μια ιστορία με ήρωες οι οποίοι συναντούν γεωμετρικά σχήματα και υπολογίζουν ποσότητες στη διάρκεια μιας συνηθισμένης μέρας. Οι ήρωες, π.χ. δύο παιδιά θα διαπίστωναν πώς οι παραπάνω έννοιες είναι άρρηκτα συνδεδεμένες με την καθημερινότητά τους και θα προέβαιναν σε εκτιμήσεις ποσοτήτων και ποικίλων τύπων υπολογισμών.