Μέτρηση και Σύγκριση Αποστάσεων-Ψάχνοντας το θησαυρό
Submitted by ltme on Tue, 04/21/2015 - 09:47Η παρούσα εργασία επεξεργάζεται τη μέτρηση αποστάσεων. Η γενική της ιδέα στηρίζεται στις απόψεις του Seymoyr Papert, στην προγραμματιζόμενη συσκευή BeBot και στην εφαρμογή Google Earth.
Ο ΣΕΥΜΟΥΡ ΠΑΠΕΡΤ (SEYMOYR PAPERT).
Ο Σέυμουρ Παπέρτ γεννήθηκε στις 29 Φεβρουαρίου 1928 στην Πρετόρια της Νοτίου Αφρικής.Είναι Επιστήμονας της Πληροφορικής και Μαθηματικός.Επίσης,μέλος του Τεχνολογικού Ινστιτούτου της Μασαχουσέτης και ένας από τους πρωτοπόρους της τεχνητής νοημοσύνης. Αποφοίτησε από το πανεπιστήμιο του Witwatersrand to 1949 όπου τρία χρόνια αργότερα έγινε κάτοχος του διδακτορικού διπλώματος στα Μαθηματικά,ενώ το 1959 αποκτά ένα ακόμη διδακτορικό στα Μαθηματικά απ’το Πανεπιστήμιο του Κέμπριτζ.Προτού γίνει ερευνητής του Τεχνολογικού Ινστιτούτου της Μασαχουσέτης,εργάστηκε ως ερευνητής σε διάφορους τομείς όπως το Εθνικό Εργαστήριο Φυσικής του Ηνωμένου Βασιλείου στο Λονδίνο,το Πανεπιστήμιο της Γενεύης,το Πανεπιστήμιο του Παρισίου.Από το 1967 ως το 1981 εργάζεται ως καθηγητής εφαρμοσμένων μαθηματικών και διευθυντής του Εργαστηρίου Επιστήμης Υπολογιστών και Τεχνητής Νοημοσύνης του Τεχνολογικού Ινστιτούτου της Μασαχουσέτης.Υπήρξε επίσης πρωτεργάτης του σχεδίου «Ένας Φορητός Υπολογιστής Ανά Παιδί»,ενώ η συμβολή του στην εδραίωση της εκπαιδευτικής γλώσσας προγραμματισμού «Logo»,ήταν καθοριστική. Ο Παπέρτ εστίασε στο πώς μπορούν να επιδράσουν οι νέες τεχνολογίες στη μάθηση και ειδικότερα στα σχολεία και διεξήγαγε έρευνα σε θεωρίες μάθησης,επηρεάζοντας σημαντικά τον τομέα της εκπαιδευτικής τεχνολογίας.Το 1960 κυκλοφορεί το βιβλίο του “Mindstorms”,όπου καταγράφει τις απόψεις και τις διαπιστώσεις του σχετικά με τη μάθηση μέσω της προσωπικής εμπειρίας. Στα μέσα της δεκαετίας του ’60 ανέπτυξε την Κατασκευαστική Θεωρία Μάθησης,επηρεασμένος από το έργο του Πιαζέ,του οποίου υπήρξε «μαθητής».Ο Παπέρτ συνεργάστηκε με τον Πιαζέ για πέντε χρόνια (1958-1963) στο Πανεπιστήμιο της Γενέυης,όπου τον βοήθησε να οικοδομήσει την θεωρία του,εφαρμόζοντας τις μαθηματικές του γνώσεις.Ο ίδιος ο Πιαζέ υποστήριξε πως κανένας δεν κατανοούσε καλύτερα τις ιδέες του από εκείνον. Ο Πιαζέ επικέντρωσε το ενδιαφέρον του στο ίδιο το άτομο κατά τη διάρκεια της εκπαιδευτικής διαδικασίας,το οποίο μαθαίνει και αλληλεπιδρά με το περιβάλλον του.Τα παιδιά «κατασκευάζουν» τις πνευματικές τους δομές,πάνω στις προϋπάρχουσες εμπειρίες τους.Οι προϋπάρχουσες αυτές νοητικές δομές των παιδιών,αλληλεπιδρούν με τις νέες εμπειρίες που προέρχονται από το περιβάλλον,αναδιατάσσονται και κατασκευάζονται νέες,μέσα από μία συνεχής διαδικασία εξισορρόπησης.Η μάθηση επομένως εκλαμβάνεται ως μία διαδικασία κατασκεύης της γνώσης,γεγονός που τονίζει τη σημασία προσφοράς στα παιδιά,ενός πλούσιου σε ερεθίσματα και αλληλεπιδραστικού περιβάλλοντος.Ο μαθητής έχει έτσι την ευκαιρία να ανακαλύψει το περιβάλλον του και να οικοδομήσει τη γνώση αυτενεργώντας μέσα σ’αυτό. Επηρεασμένος από τις θεωρίες αυτές και συμφωνώντας με την ανθρωποκεντρική θεώρηση της σκέψης,ο Παπέρτ αναπτύσσει τη θεωρία του κοστρουσκτισμού.Η θεωρία αυτή υποστηρίζει πως η μάθηση είναι μια ενεργητική διαδικασία,κατά τη διάρκεια της οποίας τα παιδιά οικοδομούν τη γνώση,μέσα από τον πειραματισμό και την εμπλοκή σε δραστηριότητες που έχουν νόημα για τα ίδια.Υποστηρίζει πως ρόλος του εκπαιδευτικού είναι να αναδιαρθώνει τα παραδοσιακά μαθήματα (π.χ.μαθηματικά),προσαρμόζοντάς τα στις ιδιαίτερες ανάγκες και δυνατότητες των παιδιών ενώ προτείνει διαφορετικούς τρόπους εκπαίδευσης των μαθητών. Ένας από τους τρόπους αυτούς,είναι το ανοιχτό υπολογιστικό περιβάλλον του μικρόκοσμου.Ο μικρόκοσμος ως εφαρμογή,αποτελείται από ένα σύνολο αντικειμένων και σχέσεων και οι χρήστες έχουν την δυνατότητα μέσα από στοιχειώδεις λειτουργίες να επιδράσουν στα αντικείμενα αυτά,να τροποποιήσουν τις μεταξύ τους σχέσεις και να δημιουργήσουν νέα.Οι μικρόκοσμοι είναι περιβάλλοντα πλούσια για εξερεύνηση και ανακάλυψη των γνώσεων με μεγάλη δυνατότητα επιλογών για τον εντοπισμό τους.Σκοπός των μικρόκοσμων είναι η ανάπτυξη των γνωστικών ικανοτήτων και των δεξιοτήτων των παιδιών και η μεταφορά των νέων γνώσεων σε διαφορετικές καταστάσεις και περιβάλλοντα.Οι μαθητές αναπτύσουν και εξασκούν την ικανότητα επίλυσης προβλημάτων,διατυπώνοντας υποθέσεις και διερευνώντας την ύπαρξη εναλλακτικών τρόπων επίλυσης ενός προβλήματος.Ο ρόλος του εκπαιδευτικού στη διαδικασία αυτή είναι συμβουλευτικός και καθοδηγητικός,καθώς γίνεται συνερευνητής και συνεργάτης των παιδιών. Ένα παράδειγμα προγραμματιστικού μικρόκοσμου,είναι η γλώσσα «Logo».Η εκπαιδευτική γλώσσα προγραμματισμού «Logo»,χρησιμοποιούνταν αρχικά από υψηλά εξειδικευμένους επιστήμονες της τεχνολογίας,ως εργαλείο σκέψης για την εξέλιξη της επιστήμης της τεχνητής νοημοσύνης.Χρησιμοποιώντας τη γλώσσα «LISP» και δημιουργώντας υποπρογράμματα τα οποία συνεχώς άλλαζαν και διόρθωναν,στόχευαν στην ανάπτυξη προγραμμάτων που θα τους βοήθουσαν στην επίλυση περίπλοκων προβλημάτων.Ο Παπέρτ εκλαβάνει τη δραστηριότητα αυτή των επιστημόνων ως μια αυθεντική διαδικασία μάθησης και συλλαμβάνει τη γλώσσα προγραμματισμού «Logo». Στο περιβάλλον της γλώσσας εμφανίζεται ένα μικρό ρομποτάκι με τη μορφή χελώνας,που μπορεί να χρησιμοποιηθεί από τα παιδιά για την επίλυση προβλημάτων.Είναι μια γλώσσα προσαρμοσμένη στο γνωστικό επίπεδο των απλών χρηστών,ώστε να μπορούν και αυτοί να εμπλέκονται σε παρόμοιες προγραμματιστικές δραστηριότητες.Μπορεί να χρησιμοποιηθεί ακόμη και από παιδιά που δε διαθέτουν γνώσεις προγραμματισμού,αφού είναι μια γλώσσα φυσική,ο συμβολικός κώδικάς της οποίας συνδέεται με την καθομιλουμένη και το χώρο των μαθηματικών.Οι αρχάριοι χρήστες αποκτούν έτσι ένα υπόβαθρο στις διαδικασίες προγραμματισμού,ενώ έχουν τη δυνατότητα μέσα από ένα δομημένο περιβάλλον να κατακτήσουν σύνθετες έννοιες,χρησιμοποιώντας την επαγωγική σκέψη.Δύνανται επίσης,λόγω της σπονδυλωτής γραμμής των προγραμμάτων,να συνεργαστούν σε ομάδες και να χωρίσουν μία εργασία σε υποεργασίες.Είναι μία γλώσσα άμεσα αλληλεπιδραστική,αφού κάθε εντολή έχει αμεσα αποτελέσματα στην οθόνη,επιτρέποντας την ανατροφοδότηση.Το δυναμικό γραφικό περιβάλλον,επιτρέπει την προσομοίωση φαινομένων και τη μελέτη μαθηματικών μοντέλων.Η χελώνα αποτελεί βιωματικό εργαλείο,μέσω του οποίου τα μικρά παιδιά μπορούν να προσεγγίσουν και να κατακτήσουν έννοιες (π.χ. αναδρομή) και να αναπτύξουν την ικανότητα επίλυσης προβλημάτων,αφού πρέπει να σκεφτούν μια σειρά εντολών που θα κάνουν τη χελώνα να τις πραγματοποιήσει.Έχουν τη δυνατότητα να εντοπίζουν τα λάθη τους,ενώ μπορούν να εμπλακούν ακόμη και σε διαδικασίες συγγραφής του κώδικα,στο δικό τους γνωστικό επίπεδο.Η γλώσσα προγραμματισμού logo,κατορθώνει αυτό που ο Παπέρτ ονομάζει «μάθηση χωρίς διδασκαλία»,αλλά μέσω της βιωματικής εμπειρίας,του πειραματισμού και της αυτοεξερεύνησης. Η σταδιακή μετεξέλιξη της γλώσσας logo είναι η εξής.Logo like γλώσσες,Lego-Logo παιχνίδια/συσκευές,Προγραμματιζόμενο Lego ΝΧΤ και Προγραμματισμός μέσω Λογισμικού ΝΧΤ,«Περιπατητές»/προγραμματιζόμενες συσκευές μέσω πλήκτρων και συμβολικού κώδικα(Bee Bot,Roamer,Lego WeDo),Γλώσσες απτού προγραμματισμού (Tern,Quetzal),Γλώσσες οπτικού προγραμματισμού (Scratch) και Λογισμικά Μικρόκοσμων (Microworlds). Τα λογισμικά αυτά,υποστηρίζουν την Κατασκευαστική Θεωρία Μάθησης του Παπέρτ,αφού διευκολύνουν ανακαλυπτικές και διερευνητικές διαδικασίες,παρέχοντας τη δυνατότητα αναπαραστάσης πολλαπλών εννοιών με τη χρήση κωδίκων και πολυμεσικών εργαλείων,ενώ υποστηρίζουν επίσης την κοινωνιογνωστική σύγκρουση. Ο Παπέρτ,χρησιμοποίησε τη νέα τεχνολογία ως εργαλείο για να αναδιαρθρώσει τα παραδοσιακά μαθηματικά και να τα προσαρμόσει στις ανάγκες και δυνατότητες των παιδιών.Μέσα από τις θεωρίες και τις έρευνές του σε νέους τρόπους διδασκαλίας,θέλησε να καταστήσει τις προηγμένες μαθηματικές έννοιες προσιτές στο ευρύ κοινό,ανάγοντας τη μαθηματική εκπαίδευση σε μια φυσική διαδικασία.
Η BEE-BOT.
Όσον αφορά την προγραμματιζόμενη συσκευή Bee-Βοt και τη διδασκαλία μαθηματικών εννοιών,η χρήση της συστήνεται για τη διδασκαλία μικρών τάξεων.Η λογική προγραμματισμού της βασίζεται στη γλώσσα logo,ενώ εκτελεί εντολές κινήσεων οι οποίες δίνονται με τα ευδιάκριτα κουμπιά που βρίσκονται στην πλάτη της.Είναι εύκολη στη χρήση,καθώς περιλαμβάνει επτά πλήκτρα απλών εντολών (ένα βήμα μπροστά-ένα πίσω,μια στροφή δεξιά-μια αριστερά,παύση,διαγραφή της μνήμης και εκκίνηση).Τα παιδιά την προγραμματίζουν για να πραγματοποιήσει της εκάστοτε διαδρομές/αποστολές της,οι οποίες μπορούν να είναι διαβαθμισμένης δυσκολίας.Έπειτα,υποστηρίζει τη διαθεματικότητα,αφού κινείται σε διαφορετικά θεματικά περιβάλλοντα (εκπαιδευτικά pad),που μπορούν να συνδεθούν με ποικιλία μαθημάτων,καλύπτοντας έτσι ένα ευρύ φάσμα δραστηριοτήτων.Επιτρέπει επίσης τη συνεργασία σε ομάδες,προωθώντας τις επικοινωνιακές δεξιότητες των παιδιών (εναλλαγή τη σειράς στην ομάδα,προώθηση συζήτησης και διαπραγμάτευσης,ανάθεση ρόλων),δεξιότητες η ανάπτυξη των οποίων αποτελεί στόχο του Αναλυτικού Προγράμματος.Όσον αφορά το Νέο Αναλυτικό Πρόγραμμα και την ενότητα της Πληροφορικής,η Bee-Bot εξυπηρετεί στόχους που σχετίζονται με το χειρισμό,τον έλεγχο και τον προγραμματισμό για την κατεύθυνση και τον προσανατολισμό του ρομπότ.Τέλος,είναι ένα εργαλείο προσιτό οικονομικά,δεν απαιτεί την ύπαρξη υπολογιστή ή άλλου είδους εξοπλισμού και κεντρίζει το ενδιαφέρον των παιδιών,τα οποία κατακτούν έννοιες και εμπλέκονται σε διαδικασίες επίλυσης προβλημάτων με παιγνιώδη τρόπο. Όσον αφορά τις δυσκολίες που προκύπτουν απ’τη χρήση της Bee-Bot,αρχικά δεν επιτέπει τη διαδικασία αποσφαλμάτωσης,αφού δεν δίνει τη δυνατότητα εντοπισμού του λάθους τμηματικά.Σε περίπτωση λάθους,η διαδικασία πρέπει να ξεκινήσει απ’την αρχή.Έπειτα,δε δίνει τη δυνατότητα παραμετροποίησης του τρόπου εφαρμογής της,αφού περιλαμβάνει περιορισμένο αριθμό κινήσεων (μπροστά,πίσω,δεξιά,αριστερά).
GOOGLE EARTH.
Το Google Earth είναι μια εφαρμογή που παρουσιάζει τη γη τρισδιάστατα.Χρησιμοποιώντας δορυφορικές εικόνες και αεροφωτογραφίες επιτρέπει στο χρήστη να περιηγηθεί ανά τον κόσμο,να αναζητήσει,να εντοπίσει και να περιηγηθεί με λεπτομέρεια σε διάφορες τοποθεσίες (σπίτια,δρόμους,οδούς,καθώς και οδηγίες για διαδρομές).Παρέχει τη δυνατότητα ζούμ,περιστροφής και κλίσης στην προβολή της γης,ενώ διαθέτει πλούσια εργαλειοθήκη που επιτρέπει τη δημιουργία νέων δεδομένων και παρέχει ποικιλία επιλογών και δυνατοτήτων,ορισμένες από τις οποίες είναι οι εξής.Η δυνατότητα εντοπισμού των συντεταγμένων μιας περιοχής,παροχής χαρτών,απεικόνισης τρισδιάστατων κτιρίων,βουνών,κοιλάδων και φαραγγιών ανά τον πλανήτη.Έπειτα,η δυνατότητα τοποθέτησης σήμανσης,ανάρτησης εικόνων,βίντεο,ήχων,καθώς και η δυνατότητα αποθήκευσης,εκτύπωσης και αποστολή τους μέσω e-mail.Γίνεται επίσης εφικτή η περιήγηση στο διάστημα (στον ουρανό,τους πλανήτες,τους αστερισμούς και τη Σελήνη) καθώς και πλήθος άλλων δυνατοτήτων.Είναι μία δωρεάν εφαρμογή,που μπορεί να λειτουργήσει σε όλα τα υπολογιστικά προγράμματα. Όσον αφορά την εκπαιδευτική διαδικασία,το λογισμικό του Google Earth παρέχει τη δυνατότητα πραγματοποίησης ποικίλων δραστηριοτήτων στα πλαίσια όλων των μαθημάτων του Αναλυτικού Προγράμματος,υποστηρίζοντας τη διαθεματικότητα.Σύμφωνα με το Αναλυτικό Πρόγραμμα,τα παιδιά χρειάζεται να εξοικειωθούν με την εργαλειοθήκη και να γνωρίσουν τις δυνατότητες που προσφέρουν τα ψηφιακά μέσα για τη καθημερινή ζωή και την επίλυση προβληματικών καταστάσεων.Είναι ιδιαίτερα ελκυστικό για τα παιδιά,αφου προσφέρει αμεσότητα,ζωντάνια και παραστατικότητα,κάνοντας την εκπαιδευτική διαδικασία ενδιαφέρουσα και διασκεδαστική.Δίνεται η δυνατότητα άμεσης οπτικοποίησης και σύνδεσης πολλαπλών πληροφοριών,καθώς και παρουσίασης τοποθεσιών στη ρεαλιστική τους μορφή,πράγμα το οποίο είναι αδύνατο να επιτευχθεί σε διαφορετικές,συμβατικές συνθήκες (χάρτες,φωτογραφίες κ.τ.λ.).Τέλος,προσφέροντας τη δυνατότητα αλλαγής της χωρικής κλίμακας από μεγάλη σε μικρή,βοηθά τα παιδιά να συσχετίσουν την αλλαγή του μεγέθους με την απόσταση καθώς οπτικοποιούν τις διαφορετικές σε μέγεθος εικόνες.
ΣΥΓΚΡΙΣΗ ΛΟΓΙΣΜΙΚΩΝ:Όσον αφορά τη σύγκριση των δύο λογισμικών,η διαδικασία που πραγματοποιήθηκε ήταν η ίδια,ωστόσο το Google Earth λειτούργησε συμπληρωματικά,για την εξοικείωση των παιδιών στη διαδικασία μέτρησης και στο ψηφιακό κόσμο.Στο Google Earth η διαδικασία μέτρησης ήταν πιο εύκολη,καθώς τα αποτελέσματα παρουσιάζονταν αμέσως χωρίς να απαιτείται ιδιαίτερη νοητική προσπάθεια.Η δυσκολία που παρουσιάστηκε αφορά την ακρίβεια της μέτρησης με το «χάρακα»,αφού απαιτείται ακριβής τοποθέτησή του κατά μήκος των διαδρομών.Στην περίπτωση που οι αριθμοί δεν βγαίνουν ακέραιοι (π.χ. 13.5 αντί 13),τα παιδιά υπολογίζουν χονδρικά.Στη συνέχεια,η νηπιαγωγός μπορεί να τους δείξει τον ακριβή υπολογισμό,που επιτυγχάνεται πατώντας δεξί «κλικ» πάνω στη δοσμένη διαδρομή,μεταβαίνοντας στις «ιδιότητες» και έπειτα στη «μέρτηση».Εκεί παρουσιάζεται με ακρίβεια ο αριθμός των μέτρων που αντιστοιχούν στην εκάστοτε διαδρομή (η νηπιαγωγός,έχει φροντίσει τα μέτρα να δίνονται σε ακέραιο αριθμό).
ΗΛΙΚΙΑ ΠΑΙΔΙΩΝ: 8 ετών (Γ’ Δημοτικού)
ΥΛΙΚΑ:Επιδαπέδιο παιχνίδι κρυμμένου θησαυρού,Bee- Bot,καρτέλες με βήματα,καλαμάκια (10 εκατοστών),οδοντογλυφίδες (6 εκατοστών),ξύλινο σπαστό μέτρο.
ΣΤΟΧΟΙ:
Παιδί και Μαθηματικά: (1)Εξοικείωση με τις άτυπες μονάδες μέτρησης μήκους (βήμα Bee-Bot,οδοντογλυφίδες,καλαμάκια). (2)Κατανόηση των διαφορετικών αποτελεσμάτων που προκύπτουν από τις διαφορετικές μονάδες μέτρησης. (3)Κατανόηση της χρήσης μιας κοινά αποδεκτής μονάδας (μέτρο) για ακριβείς μετρήσεις. Παιδί και ΤΠΕ: (1)Εξοικείωση με τις εντολές προγραμματισμού της Bee-Bot.
ΤΙΤΛΟΣ Α’ ΔΡΑΣΤΗΡΙΟΤΗΤΑΣ: Το παιχνίδι του κρυμμένου θησαυρού.
Α’ ΦΑΣΗ ΔΡΑΣΤΗΡΙΟΤΗΤΑΣ: H συγκεκριμένη δραστηριότητα προϋποθέτει ότι έχει προηγηθεί κάποια εξοικείωση των παιδιών με το προγραμματιζόμενο ρομποτάκι (Bee-Bot). Η νηπιαγωγός συγκεντώνει τα παιδιά στη γωνιά της παρεούλας και τους παρουσιάζει το Μελισσούλη,ο οποίος επέστρεψε αναζητώντας αυτή τη φορά έναν κρυμμένο θησαυρό και καλεί τα παιδιά να τον βοηθήσουν στη αναζήτησή του. Η νηπιαγωγός έχει ετοιμάσει ένα επιδαπέδιο παιχνίδι.Περιλαμβάνει ένα μεγενθυμένο παγκόσμιο χάρτη καλυμένο με plexy glass,που χωρίζεται σε τετράγωνα,καθένα απ’τα οποία είναι ίσο με το βήμα της Bee-Bot (15 εκατοστά).Το παιχνίδι περιλαμβάνει τετραγωνάκια με εικόνες,στις οποίες δίνονται εντολές για τις διαδρομές που πρέπει να ακολουθήσει ο Μελισσούλης.Σε κάθε εντολή,καλούνται να επιλέξουν τη συντομότερη,ανάμεσα σε δύο διαδρομές.Τα παιδιά τις διαβάζουν και προγραμματίζουν ανάλογα τη συσκευή.
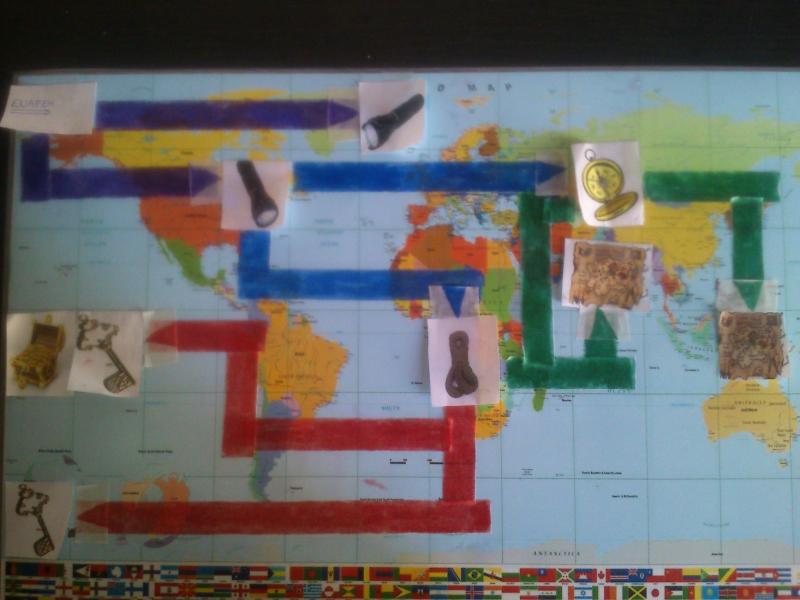
Με την έναρξη του παιχνιδιού,δίνεται μια προβληματική κατάσταση στα παιδιά,όπου καλούνται να επιλέξουν τη συντομότερη ανάμεσα σε δύο διαδρομές.Οι διαδρομές είναι καλυμμένες με χρωματιστές χαρτοταινίες,ενώ η νηπιαγωγός έχει μοιράσει στα παιδιά καρτέλες που απεικονίζουν πατούσες,για να βοηθηθούν στη μέτρηση των βημάτων. Τα παιδιά διατυπώνουν υποθέσεις σχετικά με την προβληματική κατάσταση,τις αιτιολογούν και στη συνέχεια χωρίζονται σε ομάδες των τεσσάρων ατόμων για να ξεκινήσουν το παιχνίδι.Σε κάθε ομάδα μοιράζονται ρόλοι.Δύο παιδιά καλούνται να προγραμματίσουν και να θέσουν σε λειτουργία το Μελισσούλη (ένα για κάθε διαδρομή),ένα τοποθετεί τις καρτέλες με τα βήματα στη διαδρομή που εκτελείται,ενώ το τελευτάιο,διαγράφει τη μνήμη της συσκεύης και έχει βοηθητικό ρόλο στη διαδικασία. Οι διαδρομές που δίνονται διαφέρουν ως προς τη μορφή (στροφή,ευθεία).Κάποιες φαινομενικά διαφέρουν ενώ είναι ίσες,ενώ άλλες μοιάζουν ίσες αλλά δεν είναι.Σκοπός είναι τα παιδιά να κατανοήσουν ότι η μορφή των διαδρομών δεν αντιστοιχεί με το πραγματικό τους μήκος αλλά χρειάζεται ακριβής μέτρηση.
Α' Εντολή-Διαδρομή.

Μετρώντας τα βήματα με τις καρτέλες-πατούσες.
Το παιχνίδι διεξάγεται και τα παιδιά εκτελούν τις εντολές που τους δίνονται,χρησιμοποιώντας το βήμα του Μελισσούλη ως άτυπη μονάδα μέτρησης.Σκοπός σ’αυτή τη φάση της δραστηριότητας είναι να κατανοήσουν τα παιδιά τη διαδικασία της μέτρησης αποστάσεων,να είναι σε θέση να συγκρίνουν διαδρομές και να εξοικειωθούν στη χρήση άτυπων μονάδων μέτρησης για να το επιτύχουν.
Β' Εντολή- Διαδρομή.

Γ' Εντολή- Διαδρομή.
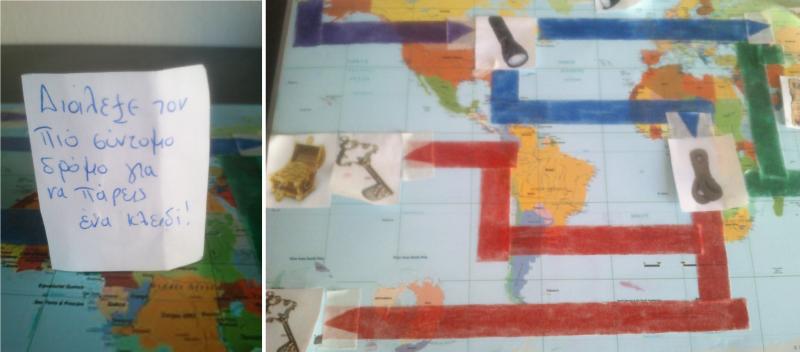
Δ' Εντολή- Διαδρομή.
B’ ΦΑΣΗ ΔΡΑΣΤΗΡΙΟΤΗΤΑΣ: Στη δεύτερη φάση της δραστηριότητας,καθώς το παιχνίδι φτάνει στο τέλος,όλες οι ομάδες έχουν πραγματοποιήσει διαδρομές και πλησιάζουν στο θησαυρό,δίνεται μία ακόμη προβληματική κατάσταση.Σύμφωνα με την εντολή,για να φτάσουν στο θησαυρό,χρειαζεται να παραγγείλουν από το μάστορα μία γέφυρα.

Εντολή για κατασκευή γέφυρας.
Η/Ο παιδαγωγός ρωτά τις ομάδες τί θα μπορούσαν να κάνουν για να δώσουν πληροφορίες στο μάστορα σχετικά με την κατασκευή της.Καταλήγουν στο ότι πρέπει να μετρήσουν το μήκος της.Η νηπιαγωγός εισάγει δύο ακόμη διαφορετικές άτυπες μονάδες για τη μέτρηση του μήκους της γέφυρας.Καλαμάκια 10 εκατοστών και οδοντογλυφίδες (με κομένες τις αιχμηρές άκρες) 6 εκατοστών.Δύο ομάδες αναλαμβάνουν να μετρήσουν την απόσταση που χρειάζεται να καλύψει η γέφυρα με τις οδοντογλυφίδες και δύο με τα καλαμάκια.Τοποθετούν στη σειρά τα υλικά,μετρώντας και σημειώνοντας παράλληλα πόσα καλαμάκια και πόσες οδοντογλυφίδες χρειάστηκαν αντίστοιχα.
 Μέτρηση γέφυρας με άτυπες μονάδες μέτρησης.
Μέτρηση γέφυρας με άτυπες μονάδες μέτρησης.
Σκοπός της εισαγωγής δύο επιπλέον διαφορετικών υλικών που θα λειτουργήσουν ως αυθαίρετες μονάδες μέτρησης,είναι να κατανοήσουν τα παιδιά ότι διαφορετικές μονάδες μέτρησης μας δίνουν διαφορετικά αποτελέσματα.Επίσης,να κατανοήσουν την ανάγκη χρησης μιας κοινά αποδεκτής μονάδας,σε περιπτώσεις που η ακρίβεια των αποτελεσμάτων καθίσταται αναγκαία.Μόλις ολοκληρωθεί η διαδικασία,συγκρίνονται τα αποτελέσματα των μετρήσεων και τα παιδιά διαπιστώνουν ότι χρειάστηκαν διαφορετικό αριθμό υλικών για τη μέτρηση της γέφυρας (περισσότερες οδοντογλυφίδες και λιγότερα καλαμάκια).Στο σημείο αυτό ακολουθεί συζήτηση των διαφορετικών αποτελεσμάτων και η/ο εκπαιδευτικός μέσα από ερωτήσεις προσπαθεί να εκμαιεύσει τις απόψεις των παιδιών. Σε περίπτωση που τα παιδιά δε μπορούν να καταλήξουν σε κάποια ιδέα,η νηπιαγωγός καθοδηγεί τη συζήτηση στη χρήση του μέτρου.Εισάγει ένα ξύλινο σπαστό μέτρο και καλεί τα παιδιά να το παρατηρήσουν ενώ κάνει ερωτήσεις. Καταλήγουν στο συμπέρασμα ότι το μέτρο είναι χρήσιμο για την ακρίβεια των αποτελεσμάτων της μέτρησης.
Γ’ ΦΑΣΗ ΔΡΑΣΤΗΡΙΟΤΗΤΑΣ: Μετά την εισαγωγή του μέτρου,τα παιδιά εξοικειώνονται με τη χρήση του.Το παρατηρούν,το επεξεργάζονται και σχολιάζουν τη διαίρεση του σε εκατοστά.Στη συνέχεια,μετρούν τόσο τη γέφυρα με τα καλαμάκια,όσο και αυτή με τις οδοντογλυφίδες και διαπιστώνουν ότι το μήκος τους είναι το ίδιο σε εκατοστά.Αλλάζει απλώς ο αριθμός των υλικών,ανάλογα με την εκάστοτε μονάδα μέτρησης που χρησιμοποιείται.Γι’αυτό είναι χρήσιμο το μέτρο,αφού προσφέρει ακριβή στοιχεία για την κατασκευή της γέφυρας. Έπειτα, επιστρέφουν για να τελειώσουν το παιχνίδι. Αφού έχουν στείλει τα στοιχεία για την κατασκευή της γέφυρας,θέτουν σε λειτουργία το Μελισσούλη για να τελειώσει την αποστολή του και να φτάσει στο θησαυρό.Μετρούν ταυτόχρονα πόσα βήματα χρειάζεται για να καλύψει τη διαδρομή,τοποθετώντας τις πατούσες. Η χρήση του μέτρου στη φάση αυτή της διαδικασίας,γίνεται για την εξοικείωση των παιδιών με αυτό και την διάκριση των άτυπων από την τυπική μονάδα μέτρησης,ενώ παράλληλα εξυπηρετεί τη μετάβαση στο επόμενο στάδιο δραστηριοτήτων (Google Earth).
ΤΙΤΛΟΣ Β’ ΔΡΑΣΤΗΡΙΟΤΗΤΑΣ:Η τελευταία αποστολή του Μελισσούλη.
ΥΛΙΚΑ:Xρήση ηλεκτρονικού υπολογιστή,χρήση λογισμικού Google Earth.
ΣΤΟΧΟΙ:
Παιδί και ΤΠΕ: (1)Εξοικείωση με την εφαρμογή του Google Earth. Παιδί και μαθηματικά: (2)Εξοικείωση με τη διαδικασία μέτρησης στον ψηφιακό κόσμο,χρησιμοποιώντας την εργαλειοθήκη («χάρακα») της εφαρμογής.
Η δεύτερη δραστηριότητα διεξάγεται την επόμενη ημέρα.Η νηπιαγωγός εισάγει τα παιδιά στο σενάριο,λαμβάνοντας ένα γράμμα από τον Μελισσούλη,ο οποίος βρίσκεται στο εξωτερικό με το θησαυρό που πήρε την προηγούμενη μέρα.Ωστόσο,υπάρχει μία τελευταία αποστολή,στην οποία χρειάζεται τη βοήθεια των παιδιών.Δεν μπορεί να ανοίξει το σεντούκι του θησαυρού και θέλει βοήθεια για να φτάσει στο εργαλείο που χρειάζεται.Έχει δώσει πληροφορίες για το πού ακριβώς βρίσκεται.Η νηπιαγωγός κάνει στα παιδιά τις εξής ερωτήσεις: Πώς νομίζετε ότι μπορούμε να δούμε πού βρίσκεται ο Μελισσούλης; Γνωρίζετε κάποιον εύκολο τρόπο ώστε να μεταφερθούμε εκεί που βρίσκεται και να τον βοηθήσουμε; Στη συνέχεια προτείνει στα παιδιά να περάσουν στη γωνιά της πληροφορικής,όπου έχει ανοιχτό το λογισμικό του Google Earth.Τους κάνει μια παρουσίαση και περιήγηση στο λογισμικό.Έπειτα συμπληρώνει στην αναζήτηση της περιοχής τις πληροφορίες που έδωσε ο Μελισσούλης για το πού ακριβώς βρίσκεται.Πατούν το πλήκτρο της αναζήτησης και μεταβαίνουν στην περιοχή.Εκεί η νηπιαγωγός έχει προσχεδιάσει συγκεκριμένες διαδρομές,τοποθετώντας σημεία και γράφοντας οδηγίες για κάθε διαδρομή.Τα παιδιά καλούνται να εκτελέσουν τις εντολές μετρώντας τις διαδρομές και επιλέγοντας τη συντομότερη. Αρχικά η/ο εκπαιδευτικός εξοικειώνει τα παιδιά με τη χρήση του χάρακα από την εργαλειοθήκη της εφαρμογής,που χρησιμοποιείται ως τυπική μονάδα μέτρησης.Τους περιγράφει τη διαδικασία που χρειάζεται να ακολουθήσουν για τη μέτρηση των διαδρομών.Επιλέγουν από την εργαλειοθήκη το εικονίδιο του «χάρακα» και έπειτα την επιλογή της «διαδρομής».Στη συνέχεια,τοποθετούν τον κέρσορα πάνω στο σημείο εκκίνησης της διαδρομής.Εμφανίζεται μια κίτρινη γραμμή η οποία αυξομειώνεται ανάλογα με την κίνηση του κέρσορα.Τοποθετούν τη γραμμή κατά μήκος της διαδρομής και πατώντας πάνω στο σημείο προορισμού,τους δίνονται τα μέτρα που αντιστοιχούν στη διαδρομή.Καθώς κάθε φορά καλούνται να επιλέξουν τη συντομότερη ανάμεσα σε δύο διαδρομές,μετρούν το μήκος και των δύο και μεταβαίνουν ανάλογα στην επόμενη.


Μέτρηση διαδρομής με την κίτρινη γραμμή του «χάρακα».
Λόγω έλλειψης υπολογιστών τα παιδιά κάθονται ανά ομάδες των τεσσάρων ατόμων.Κάθε μέλος της ομάδας εκτελεί δύο εντολές και στη συνέχεια παραχωρεί τη θέση του στον επόμενο για να συνεχίσει τη διαδρομή.Κατά τη διάρκεια της διαδικασίας,ενώ η ομάδα εκτελεί τις διαδρομές,τα υπόλοιπα παιδιά εξοικειώνονται με το λογισμικό του google earth στον υπολογιστή της νηπιαγωγού.Εξερευνούν διάφορες χώρες και περιηγούνται σ’αυτές σε αναλογική και τρισδιάστατη μορφή. Αφού ολοκληρωθεί η διαδικασία και όλες οι ομάδες φέρουν σε πέρας την αποστολή τους,επιστέφουν στη γωνιά της παρεούλας για να διατυπώσουν τις απόψεις τους. Ακολουθεί συζήτηση γύρω από τις εντυπώσεις των παιδιών σχετικά με τις δύο διαδικασίες. Τα συμπεράσματα στα οποία καταλήγουν είναι αρχικά ότι και στις δύο δραστηριότητες πραγματοποιήθηκε η ίδια διαδικασία,ωστόσο άλλαζαν τα διαφορετικά μέσα (Bee-Bot και Google Earth) και οι μονάδες μέτρησης (βήμα bee-bot,καλαμάκια,οδοντογλυφίδες,μέτρα).Και στις δύο ωστόσο χρησιμοποιήθηκε ως τυπική μονάδα μέτρησης το μέτρο.Τέλος,τα παιδιά κατανοούν τη διάκριση ανάμεσα στις άτυπες και τυπικές μονάδες μέτρησης,το γεγονός ότι οι διαφορετικές μονάδες μας δίνουν διαφορετικά αποτελέσματα,καθώς και την ανάγκη χρήσης της τυπικής μονάδας (μέτρο) για την ακρίβεια των αποτελεσμάτων.
-Διαδίκτυο
-Βιβλίο: John A. Van De Walle