Στο βιβλίο της Ευγενίας Κολέζας (2000), αναφέρεται ο ορισμός του Fischbein για τα γεωμετρικά σχήματα. Συγκεκριμένα ως γεωμετρικά σχήματα ορίζονται οι νοητικές οντότητες (mental entities), όπου ο χαρακτήρας τους είναι και εννοιολογικός (conceptual) ,αλλά και σχηματικός (figural). Ως αποτέλεσμα αυτής της περίπτωσης προκύπτει ότι τα γεωμετρικά σχήματα τα ονομάζει σχηματικές έννοιες (Figural concepts). Ουσιαστικά τα γεωμετρικά σχήματα ως έννοια αποτελούνται από τον ορισμό (the definition), την εικόνα (the images) και τη σχηματική έννοια (the figural concept). Ο ίδιος το εξηγεί αυτό με τον εξής τρόπο: “Ένα σχέδιο (drawing/the image) δεν είναι αυτό το ίδιο το γεωμετρικό σχήμα, αλλά μια γραφική συγκεκριμένη υλική παρουσίασή του. Το γεωμετρικό σχήμα είναι η ιδέα που αντιστοιχεί στο σχέδιο, η αφηρημένη ιδεατή, εξαϋλωμένη οντότητα (the figural concept) που καθορίζεται επακριβώς από τον ορισμό (the definition).”

Ένας ακόμα απλός ορισμός που υπάρχει για τα γεωμετρικά σχήματα είναι ότι τα σχήματα είναι ένα σύνολο σημείων στο χώρο και σύμφωνα με την ευκλείδεια γεωμετρία (Αργυρόπουλος Ηλίας, Βλάμος Παναγιώτης, Κατσούλης Γεώργιος, Μαρκάτης Στυλιανός, Σιδέρης Πολυχρόνης, 2000), τα βασικά στοιχεία είναι το σημείο, η ευθεία και το επίπεδο.

ΣΤΟΧΟΙ-Γιατί διδάσκουμε αυτή την μαθηματική έννοια

Αρχικά, σύμφωνα με το νέο αναλυτικό πρόγραμμα, τα παιδιά θα μπορούν, μέσω της διδασκαλίας αυτής της μαθηματικής έννοιας:

1. Να αναγνωρίζουν, να ονομάζουν και να ταξινομούν τα βασικά επίπεδα γεωμετρικά σχήματα με βάση τα χαρακτηριστικά τους και σε ποικιλία θέσεων, μεγεθών και προσανατολισμών

1. Να περιγράφουν επίπεδα γεωμετρικά σχήματα, χρησιμοποιώντας τα στοιχεία και τις ιδιότητες

1. Να κατασκευάζουν επίπεδα γεωμετρικά σχήματα με διάφορα μέσα

1. Να συνθέτουν και να αναλύουν απλά επίπεδα γεωμετρικά σχήματα σε δύο ή περισσότερα μέρη

Επιπρόσθετα κάποιοι άλλοι στόχοι που τίθενται είναι οι παρακάτω:

1. Να αντιλαμβάνονται τα αντικείμενα και τις μεταξύ τους σχέσεις μέσω της κιναισθησίας.

1. Να χτίζουν συστηματικές γνώσεις για τις χωρικές ιδιότητες και σχέσεις των αντικειμένων.

1. Να αντιστοιχίζουν χώρους, οι οποίοι βρίσκονται σε διαφορετικά μεγέθη.

1. Να αναπτύσσουν δεξιότητες για να δημιουργούν και να χρησιμοποιούν διάφορες χωρικές αναπαραστάσεις.

1. Να αναγνωρίσουν και να καταλάβουν ότι σχετίζεται με τα μαθηματικά και το οποίο υπάρχει στο γεωμετρικό περιβάλλον. (Τζεκάκη, 2010)

Ως προς το “γεωμετρικό συλλογισμό”, που έχει να κάνει με το πώς οργανώνουμε και επεξεργαζόμαστε έναν βιωμένο χώρο με βάση γεωμετρικά μοντέλα, τα παιδιά θα μπορούν :

1. Να αναγνωρίζουν, να περιγράφουν και να αναλύουν τις κατηγορίες, τις ιδιότητες και τις ιδιότητες των κατηγοριών των γεωμετρικών σχημάτων.

1. Να αναλύουν και να συνθέτουν ή να ανασυνθέτουν σε άλλα σχήματα. (Τζεκάκη, 2010)

Διδάσκοντας τη συγκεκριμένη μαθηματική έννοια, τα παιδιά θα μπορέσουν να συνειδητοποιήσουν το γεγονός, ότι τα γεωμετρικά σχήματα μπορούμε να τα συναντήσουμε παντού στην καθημερινή μας ζωή και ακόμα μπορούμε να τα χρησιμοποιήσουμε συνειδητά ή ασυνείδητα για ποικίλους λόγους, είτε ατομικούς, είτε συλλογικούς.

Βάση για τη σχεδίαση δραστηριοτήτων

Στάδια VAN HIELE

Επίπεδο 1: (αναγνώριση/recognition) Τα παιδιά αντιλαμβάνονται τα γεωμετρικά σχήματα ως καθολικά (Gestalt) και όχι σε σχέση µε τα χαρακτηριστικά τους. Για την περιγραφή των σχημάτων χρησιμοποιούν οπτικά μέσα (π.χ. αναγνωρίζουν ένα ορθογώνιο επειδή μοιάζει µε πόρτα).

Επίπεδο 2: (ανάλυση/analysis) Τα παιδιά αναγνωρίζουν τα σχήματα µε τη βοήθεια των χαρακτηριστικών τους, µπορούν να τα ανακαλύπτουν και να τα περιγράφουν, αλλά δεν µπορούν να τα ορίσουν. Αν τα ρωτήσουµε γιατί αυτό το σχήµα είναι ορθογώνιο, τότε θα µας πουν κάποια από τα χαρακτηριστικά του ορθογωνίου (όπως: τα τετράγωνα έχουν τέσσερις ορθές γωνίες κτλ).

Επίπεδο 3: (διάταξη/order) Τα παιδιά μπορούν να κατηγοριοποιήσουν τα σχήματα και τα χαρακτηριστικά τους και αρχίζουν να κατανοούν το ρόλο του ορισµού, αλλά δεν μπορούν να δουλέψουν στα πλαίσια του μαθηματικού συστήματος.

Επίπεδο 4: (παραγωγικός συλλογισµός/deduction) Τα παιδιά καταλαβαίνουν τη σηµασία του παραγωγικού συλλογισµού και τους ρόλους των αξιωµάτων, των θεωρηµάτων και της απόδειξης.

Επίπεδο 5: (αυστηρότητα/rigor) Τα παιδιά μπορούν να κατανοήσουν και είναι σε θέση να κάνουν αφηρηµένους παραγωγικούς συλλογισµούς.

(Κολέζα, 2000, Van De Walle, 2007)

ΠΡΟΤΑΣΗ ΣΕΝΑΡΙΟΥ ΔΙΔΑΣΚΑΛΙΑΣ

Τίτλος: Πως γεννιούνται τα σχήματα;

Συμβατότητα με ΔΕΠΠΣ & ΑΠΣ: Το συγκεκριμένο κεφάλαιο εντάσσεται στην ενότητα του ΑΠΣ «Χώροι και γεωμετρία» και αντιστοιχεί στο γενικότερο στόχο της ανάλυσης επίπεδων γεωμετρικών σχημάτων σε στοιχεία και ιδιότητες, καθώς και οι κατασκευές επίπεδων γεωμετρικών σχημάτων με διάφορα μέσα (στη περίπτωσή μας με τη χρήση ψηφιακών λογισμικών).

Σκοπός: Περιγραφή των επίπεδων γεωμετρικών σχημάτων με αναφορά στα στοιχεία τους και στις ιδιότητες. Να οδηγούνται βαθμιαία και σε κατηγορίες στην ίδια ομάδα σχημάτων. Να χρησιμοποιούν ψηφιακά λογισμικά για να κατασκευάζουν σχήματα και να προσεγγίσουν άτυπα ιδιότητες και σχέσεις. Τέλος να συγκρίνουν και να συζητούν τις κατασκευές τους.

Στόχοι: Να δημιουργηθούν καταστάσεις, όπου τα παιδιά χρειάζεται να αναγνωρίσουν γεωμετρικά σχήματα (Google Earth). Να αναγνωρίζουν τα σχήματα που είναι όμοια, να τα αντιστοιχούν και να περιγράφουν τις ιδιότητες τους (Geogebra). Μετά το τέλος των κατασκευών να ενθαρρύνουν συζητήσεις που αναδεικνύουν ιδιότητες των σχημάτων (Ενότητα: παιδί και μαθηματικά).

Οριζόντιες ικανότητες: Γεωμετρική ικανότητα και ανάπτυξη κριτικής ικανότητας και δημιουργικότητας.

Εκπαιδευτικά λογισμικά, υπηρεσίες ΤΠΕ και δικτυακοί τόποι: Στις δραστηριότητες μας θα χρησιμοποιήσουμε δύο ψηφιακά λογισμικά, το Geogebra και το Google Earth και στο τέλος τον συνδυασμό των δύο αυτών λογισμικών. Βέβαια οι δραστηριότητες είναι ευέλικτες και θα μπορούσαν να διεκπεραιωθούν και με άλλα ψηφιακά λογισμικά.

Εκπαιδευτική μέθοδος: Διερευνητική και ανακαλυπτική μάθηση, μέσα από τη παρατήρηση, το δομημένο ψηφιακό παιχνίδι, την ομαδοσυνεργατική και δυομαδική εργασία και τις ερωτήσεις-απαντήσεις.

Διάρκεια: Περίπου 40 λεπτά η κάθε δραστηριότητα, ανάλογα με το ενδιαφέρον των παιδιών.

Γενική περιγραφή: Βασικός στόχος είναι να κατανοήσουν τα παιδιά πως γεννιούνται-δημιουργούνται τα γεωμετρικά σχήματα-πολύγωνα στα συγκεκριμένα ψηφιακά λογισμικά.

Δυσκολίες παιδιών στη κατανόηση του θέματος: Οι έννοιες αυτές είναι δύσκολο να κατανοηθούν άμεσα από τα παιδιά χρειάζεται χρόνος και μάλιστα να έχουν προηγηθεί οι ανάλογες προετοιμασίες. Για την ορθή ροή των διδακτικών ενοτήτων, κρίνεται αναγκαία η συμβολή τόσο του αναλυτικού προγράμματος της νηπιαγωγού όσο και του ΔΕΠΠΣ, αλλά και άλλων πιλοτικών προγραμμάτων, όπως είναι το «digital school». Κάποια παιδιά είναι ήδη ενημερωμένα στο βασικό επίπεδο, από το οικογενειακό περιβάλλον με τη χρήση των ΤΠΕ και συγκεκριμένα το χειρισμό τέτοιων λογισμικών, και μέσα από τις δραστηριότητες εύκολα ενισχύουν τις ήδη προϋπάρχουσες γνώσεις τους για το θέμα και αποκτούν μια πληρέστερη άποψη. Βέβαια υπάρχουν και τα παιδιά που δεν έχουν κατακτήσει ούτε τις βασικές δεξιότητες χειρισμού ενός υπολογιστή. Έτσι είναι εύλογο ότι μέσα από αυτές τις δραστηριότητες θα γίνουν αντιληπτές αυτές οι διαφορές και κατά συνέπεια οι άτυπες γνώσεις των μαθητών, με αποτέλεσμα να ακολουθήσουν και οι ανάλογες δραστηριότητες.

Προαπαιτούμενη γνώση: Οι μαθητές αναμένεται να είναι εξοικειωμένοι με τη χρήση ηλεκτρονικών υπολογιστών, καθώς και με τα βασικά χαρακτηριστικά των γεωμετρικών σχημάτων - πολυγώνων.

Περιγραφή δραστηριοτήτων

Δραστηριότητα 1: Σχεδιάσαμε μια μπερδεμένη διαδρομή στο Google Earth με αρχή και τέλος, στην οποία είναι κρυμμένα κάποια γεωμετρικά σχήματα. Παρακινούμε τα παιδιά να παρατηρήσουν την εικόνα και να εξωτερικεύσουν τις σκέψεις τους, γι’ αυτό που απεικονίζεται. Ζητάμε από εκείνα να κάνουν τη διαδρομή από την αρχή ως το τέλος, διασχίζοντας το χάρτη (διεκπεραιώνοντας την διαδρομή που επιθυμεί η κάθε ομάδα αρκεί να ξεκινάει από την αρχή και να φτάνει στο τέλος) και να ανακαλύψουν τα κρυμμένα σχήματα που υπάρχουν. Αφού αναγνωρίσουν τα σχήματα και μας τα ονομάσουν, καλούνται να περιγράψουν τις ιδιότητες τους (ίσες πλευρές, μεγαλύτερες κλπ) και να κάνουν αναφορά στα στοιχεία τους (γωνίες, πλευρές, κορυφές).

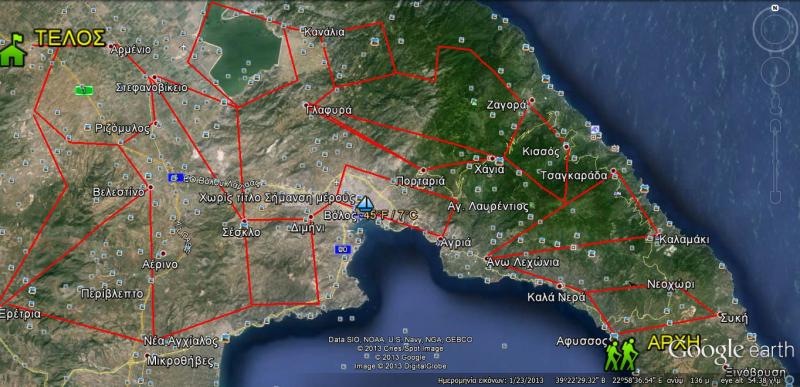
Ενδεικτικές ερωτήσεις που προωθούν την εξέλιξη της δραστηριότητας :

«Για παρατήρησε αυτή την εικόνα. Πες μου τι βλέπεις;» , «Νομίζεις ότι οδηγούν κάπου αυτά τα σχήματα;» , « Νομίζεις ότι είναι κάποιος χάρτης;» , «Από πού μπορείς να ξεκινήσεις;» «Που νομίζεις ότι μπορεί φτάσεις στο τέλος;» , «Μήπως νομίζεις ότι πρέπει να ξεκινήσεις από εκεί που είναι τοποθετημένα τα ανθρωπάκια και να φτάσεις εκεί που είναι το σπιτάκι;» , «Έχεις πολλές επιλογές για να κάνεις αυτή τη διαδρομή;» «Εσύ ποιο δρόμο θα διαλέξεις;» , «Δείξε μου ποια διαδρομή ακολουθείς» , «Καθώς κάνεις αυτή τη διαδρομή συναντάς κάποια σχήματα;» , «Μπορείς να μου τα δείξεις και να τα ονομάσεις;», «Πώς το κατάλαβες ότι είναι αυτό το σχήμα;» , «Τι ξέρεις εσύ για αυτό το σχήμα;» , «Μήπως θυμάσαι και κάτι άλλο;» , «Και ποια η διαφορά του με αυτό το σχήμα;» , «Βλέπεις κάποιες ομοιότητες;»

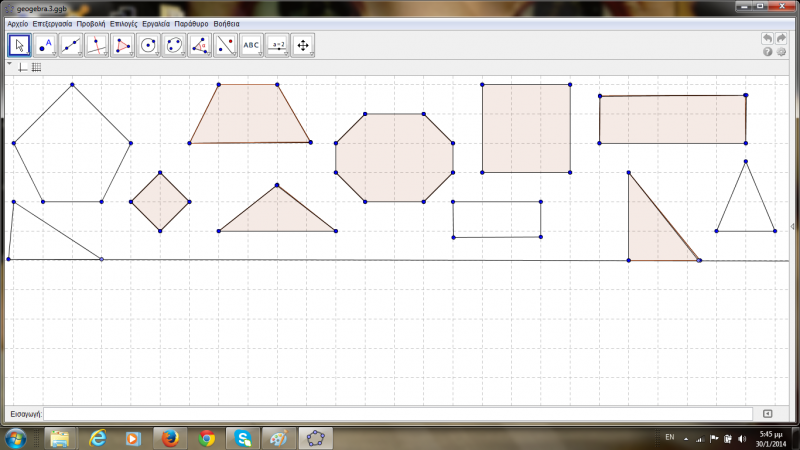
Δραστηριότητα 2: Χωρίζουμε την επιφάνεια σε δύο μέρη. Στο κάτω μέρος, δημιουργήσαμε κάποια γεωμετρικά σχήματα. Στο πάνω μέρος σχηματίσαμε ακριβώς τα ίδια σχήματα με το κάτω μέρος, αλλά και κάποια επιπρόσθετα. Ζητάμε από τα παιδιά να αναγνωρίσουν ποια σχήματα είναι ίδια στο πάνω και κάτω μέρος. Έπειτα τους παροτρύνουμε να μετακινήσουν τα κάτω σχήματα στα αντίστοιχα σχήματα από το πάνω μέρος, που εφάπτονται. Υπάρχουν κάποια σχήματα στο πάνω μέρος που θα περισσέψουν. Αφού γίνει η αντιστοίχιση, ζητάμε από τα παιδιά να περιγράψουν τις ιδιότητες των σχημάτων αυτών.

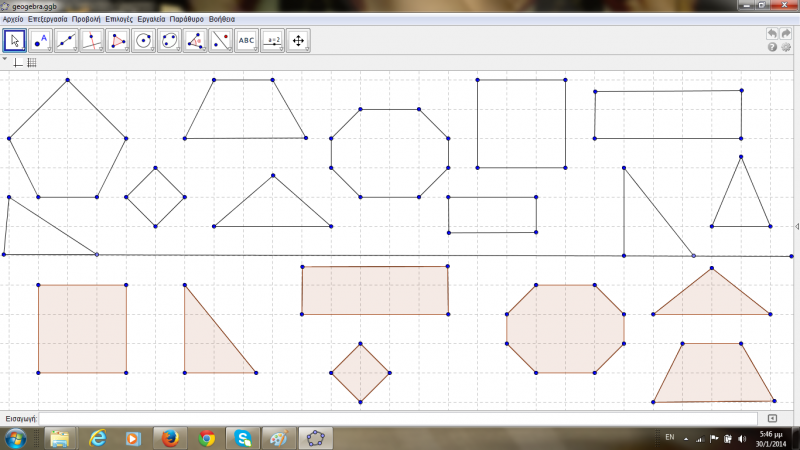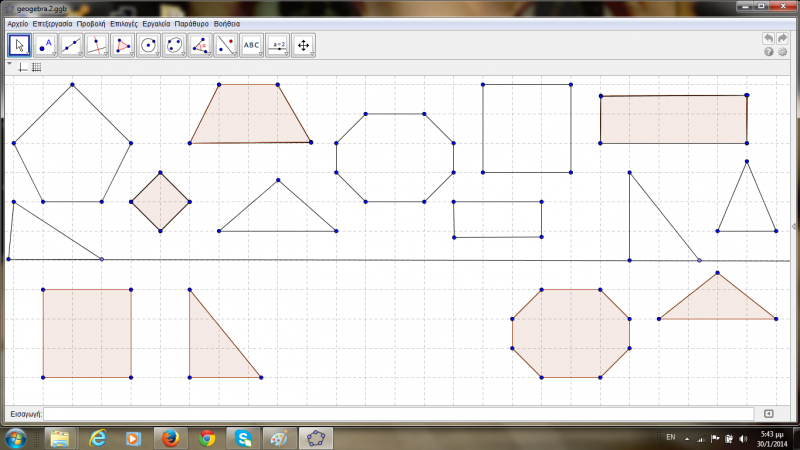Ενδεικτικές ερωτήσεις που προωθούν την εξέλιξη της δραστηριότητας :

«Τι βλέπεις στην οθόνη;» , «Ποια σχήματα αναγνωρίζεις;» , «Τα σχήματα που βρίσκονται στο κάτω μέρος, ταιριάζουν με κάποια από τα πάνω;» , «Προσπάθησε να μετακινήσεις τα σχήματα από το κάτω μέρος σε αυτά που ταιριάζουν από το πάνω.» , «Είσαι σίγουρος/η ότι αυτό που έκανες είναι σωστό;», «Γιατί το πιστεύεις αυτό;» , «Πώς κατάλαβες ότι αυτό το σχήμα ταιριάζει με αυτό που διάλεξες;» , «Τι ξέρεις εσύ για αυτό το σχήμα;» , «Γιατί νομίζεις ότι δεν ταιριάζουν αυτά τα δύο σχήματα;».

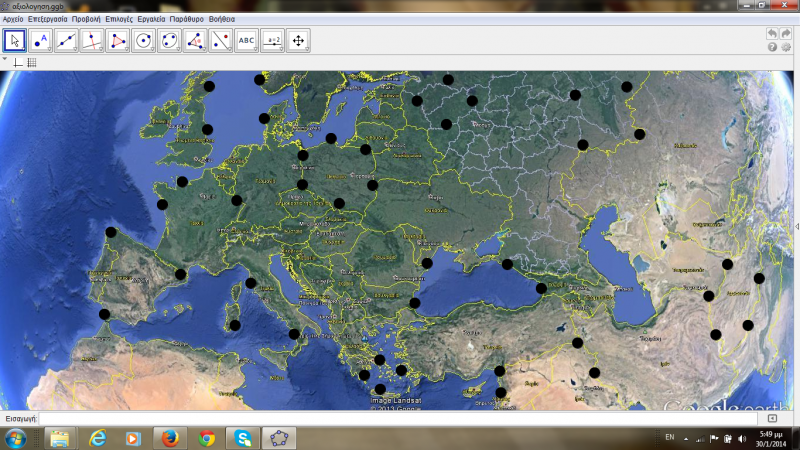
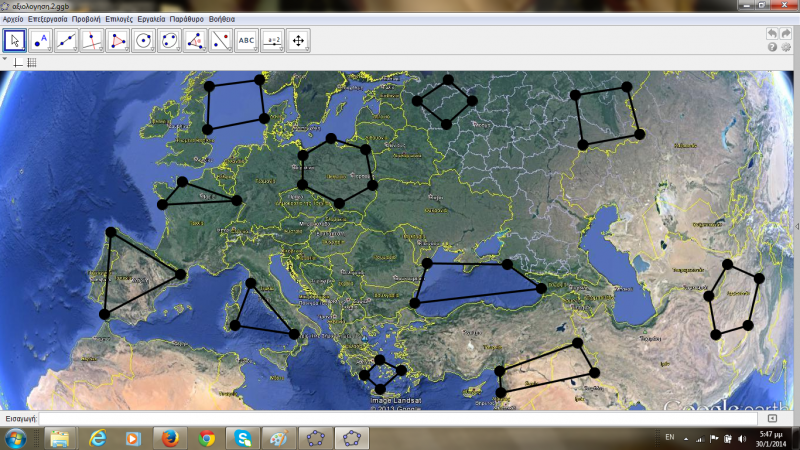
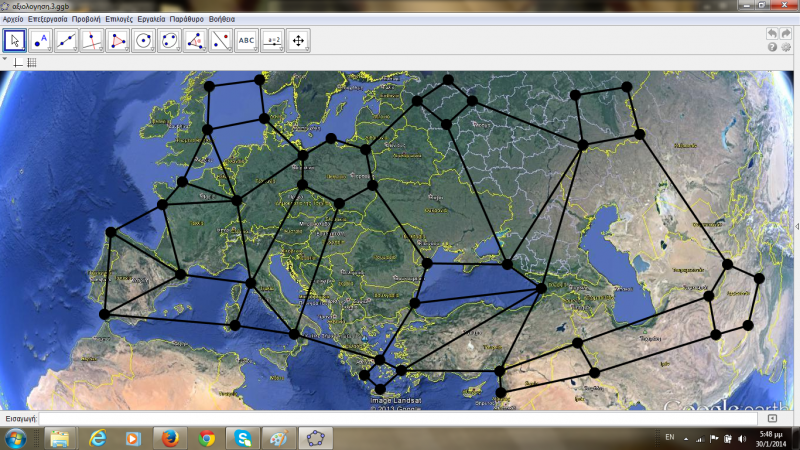
Αξιολόγηση-Δραστηριότητα 3: Για την αξιολόγηση των δραστηριοτήτων που προαναφέρθηκαν, χρησιμοποιούμε το συνδυασμό των δύο αυτών λογισμικών. Έτσι εισαγάγαμε ένα χάρτη της Ευρώπης από το Google Earth στο Geogebra. Στη συνέχεια τοποθετήσαμε κουκίδες σε διάφορα σημεία του χάρτη και ζητήσαμε από τα παιδιά να τις ενώσουν και να μας πουν τι σχήματα νομίζουν ότι προκύπτουν. Μπορούν να ενώσουν όποιες τελείες επιθυμούν και να δημιουργήσουν όσα σχήματα θέλουν. Μετά το τέλος των κατασκευών ενθαρρύνουμε συζητήσεις που μέσα από αυτές τα παιδιά αναδεικνύουν ιδιότητες των σχημάτων.

Ενδεικτικές ερωτήσεις που προωθούν την εξέλιξη της δραστηριότητας :

«Τι νομίζεις ότι μας δείχνει αυτός ο χάρτης;» , «Τι νομίζεις ότι θα συμβεί , αν ενώσουμε τις κουκκίδες;» , « Για δοκίμασέ να ενώσεις με ευθείες γραμμές όλες τις κουκκίδες.» , «Τι παρατηρείς;» , «Πώς νομίζεις ότι προέκυψαν αυτά τα σχήματα;» , «Ποια είναι αυτά τα σχήματα;» , « Από πού τα αναγνώρισες;» , «Πάντα έχει x γωνίες- x πλευρές;»

Αποτίμηση:

Κάναμε χρήση του δυναμικού λογισμικού Google Earth, για τη διδασκαλία και μάθηση των μαθηματικών και συγκεκριμένα των γεωμετρικών σχημάτων. Με τις δυνατότητες που μας παρέχει το Google Earth, μπορούμε να απεικονίσουμε εικόνες από το πλανήτη και το διάστημα, να ενημερωθούμε για τις καιρικές συνθήκες και τις γεωγραφικές συντεταγμένες, να παρατηρήσουμε τον κατακόρυφο και οριζόντιο διαμελισμό, να ερευνήσουμε χάρτες, θάλασσες, ωκεανούς και ιστορικές εικόνες, να τοποθετήσουμε σήμανση μέρους, αποθήκευσης, αποστολής μέσω e-mail και εκτύπωσης, υπάρχει δυνατότητα ανάρτησης εικόνων, βίντεο και αποσπασμάτων ήχου, καθώς και δυνατότητα ζουμ, κλίσης και περιστροφής. Επιλέξαμε τη χρήση του συγκεκριμένου λογισμικού, καθώς είναι ευέλικτο στο σχεδιασμό γεωμετρικών σχημάτων μέσω του σχεδιασμού διαδρομής και σήμανσης μέρους. Χρησιμοποιήσαμε το χάρτη της ευρύτερης περιοχής του Πηλίου και σχεδιάσαμε διαδρομές, στις οποίες εσκεμμένα προέκυπταν από εμάς γεωμετρικά σχήματα. Τα παιδιά επιλέγουν μόνα τους τη διαδρομή που θα ακολουθήσουν από την αρχή ως το τέλος και καλούνται να μας πουν τα γεωμετρικά σχήματα που συνάντησαν κατά τη διάρκεια αυτής, να περιγράψουν τις ιδιότητές τους και να αναφέρουν τα στοιχεία τους. Στην ουσία τα παιδιά δεν κάνουν συστηματική χρήση του υπολογιστή, καθώς γίνονται παρατηρητές της δραστηριότητας που τους έχουμε ήδη ετοιμάσει και μέσα από την οξύτητα του νου προσπαθούν να ανακαλύψουν τα κρυμμένα σχήματα.

Επίσης χρησιμοποιήσαμε και το δυναμικό λογισμικό μαθηματικών Geogebra, για τη διδασκαλία και μάθηση των μαθηματικών, και συγκεκριμένα για τη γεωμετρία. Γίνεται αντιληπτό ότι τα παιδιά κατανοούνε καλύτερα τις γεωμετρικές έννοιες και ενισχύεται ο προσανατολισμός και η διερεύνηση τους. Επιπροσθέτως χρησιμοποιείται για ενεργή και προσανατολισμένη σε προβλήματα διδασκαλία. Επιλέξαμε τη χρήση του συγκεκριμένου λογισμικού, καθώς είναι αρκετά ευέλικτο στο σχεδιασμό των γεωμετρικών σχημάτων και τα παιδιά μπορούν να κατανοήσουν καλύτερα τη κατασκευή και τις ιδιότητές τους. Αρχικά σχεδιάσαμε εμείς τα σχήματα για να μπορέσουν τα παιδιά να τα συγκρίνουν και να διαπιστώσουν ποια ταυτίζονται μεταξύ τους ανάλογα με τα χαρακτηριστικά τους και ποια είναι ανόμοια. Έτσι κατανοούν και την ύπαρξη ποικίλων σχημάτων. Είναι εύλογο ότι μέσα από αυτή τη δραστηριότητα διεγείρεται ο πειραματισμός των παιδιών, κάνοντας ενεργή χρήση του υπολογιστή.

Τέλος συνδυάσαμε τα δύο λογισμικά Google Earth και Geogebra. Αρχικά τοποθετήσαμε κουκίδες σε διάφορα σημεία του χάρτη και ζητήσαμε από τα παιδιά να τις ενώσουν και να μας πουν τι σχήματα νομίζουν ότι προκύπτουν. Μπορούν να ενώσουν όποιες τελείες επιθυμούν και να δημιουργήσουν όσα σχήματα θέλουν. Αφού τα κατασκευάσουν, συζητάμε με τα παιδιά τις ιδιότητες των σχημάτων. Με το συνδυασμό τους εκμεταλλευόμαστε τις δυνατότητες και των δύο λογισμικών. Από τη μια μεριά το geogebra είναι ελεύθερο, μπορούμε να το εξελίξουμε, και ειδικεύεται αποκλειστικά στα μαθηματικά, ενώ το Google earth είναι περιορισμένο σε σχέση με το αντικείμενο το μαθηματικών και συγκεκριμένα των γεωμετρικών σχημάτων. Επίσης, γίνεται αντιληπτό ότι από αυτό τον συνδυασμό τα παιδιά μπορούν να αναπτύξουν την λεπτή κινητικότητα, καθώς μέσω του χειρισμού του υπολογιστή δημιουργούν σχήματα και δύναται να τα διαφοροποιήσουν, εξερευνώντας έτσι τις πολλαπλές δυνατότητες που τους παρέχονται αναπτύσσοντας στο μέγιστο τη φαντασία τους. Παράλληλα, μπορούν να εξοικειωθούν ποικιλόμορφα με τις διάφορες μορφές των γεωμετρικών σχημάτων, καθώς και με την ευρύτερη χρήση του ηλεκτρονικού υπολογιστή, ενώ η όλη διαδικασία ενισχύεται με την καθοδήγηση του εκπαιδευτικού, αφού η αλληλεπίδραση είναι έντονη.