ΟΡΙΣΜΟΣ ΤΗΣ ΜΑΘΗΜΑΤΙΚΗΣ ΕΝΝΟΙAΣ: Αρχικά για να κατανοήσει το παιδί την έννοια της πρόσθεσης υπάρχουν τρία στοιχεία που θα το βοηθήσουν στην ανάπτυξη αυτής της γνώσης. Αυτά τα στοιχεία είναι τα εξής: Πρώτον οι σταθερές σχέσεις των αριθμών της πρώτης δεκάδας που αποτελούν την βάση για την ανάπτυξη κάθε πρόσθεσης. Με τον όρο σταθερές σχέσεις ονομάζουμε τους συνδυασμούς που δίνουν τα αθροίσματα ως το 10. Αυτή η αντίληψη είναι κρίσιμη για την κατανόηση όλων των επόμενων βημάτων. Δεύτερον οι πράξεις με αριθμούς μετά την πρώτη δεκάδα, όπου οι πράξεις αυτές αποτελούν έναν μεγάλο αριθμό από σχέσεις ανάμεσα στους αριθμούς της πρώτης δεκάδας που στηρίζουν και τις επόμενες μονάδες. πχ ( 3+4=7) και πχ το (4 είναι 2+2 και 3+1) έτσι (300 +400=700). Και τέλος, το τρίτο στοιχείο αφορά το πλαίσιο μέσα στο οποίο εμφανίζονται τα προβλήματα, το οποίο παρουσιάζει διαφορές ως προς τον τρόπο με τον οποίο γίνεται κατανοητό από τα παιδιά αλλά και ως προς το περιεχόμενο του. Υπάρχουν τρία βασικά σχήματα για προβλήματα με δύο ποσότητες και είναι τα εξής. Συνδυάζω-αλλάζω-συγκρίνω. Είναι λοιπόν σημαντικό από την μικρή ηλικία να ασκηθούν στην χρήση υλικού ή σχεδίων ώστε βαθμιαία να κατακτήσουν τις σχέσεις αυτές. Κατάλληλο υλικό για τις δραστηριότητες τις πρόσθεσης είναι το υλικό που ενώνεται και χωρίζεται ώστε τα παιδιά να αντιληφθούν τη δράση που αφορά την πρόσθεση. (κύβοι, κάρτες με δύο χρώματα, τετράγωνα χωρισμένα σε μέρη) (Τζεκάκη, 2011)
ΣΥΣΧΕΤΙΣΗ ΜΕ ΑΛΛΕΣ ΕΝΝΟΙΕΣ: Σύμφωνα με τη Nunes και τους συνεργάτες της, η έννοια της πρόσθεσης είναι στενά συνδεδεμένη με εκείνη της προσθετικής σύνθεσης καθώς η πρώτη αποτελεί απαραίτητο κεκτημένο για την κατανόηση της δεύτερης. Για τους ίδιους τα παιδιά, όταν ξεκινούν να προσεγγίζουν την πρόσθεση, χρησιμοποιούν την στρατηγική της ολικής απαρίθμησης προκειμένου να βρουν το άθροισμα δυο προσθετέων. Πιο συγκεκριμένα, αν πρέπει να βρουν το άθροισμα της πρόσθεσης 4+2, τότε θα φτιάξουν μια συλλογή από 4 αντικείμενα και μια από 2 αντικείμενα και θα τα μετρήσουν αρχίζοντας από τη πρώτη συλλογή και περνώντας στην άλλη. Αργότερα, τα παιδιά χρησιμοποιούν μια πιο οικονομική στρατηγική- αυτή της μερικής απαρίθμησης/ μνήμης, κάτι που γίνεται αντιληπτό από τους αναπτυξιακούς ψυχολόγους ως μια αναπτυξιακή πρόοδος. Εδώ τα παιδιά, έχοντας κατά νου το πρόβλημα πρόσθεσης που προηγήθηκε, θα φτιάξουν ένα σύνολο από 2 αντικείμενα και θα αρχίσουν να απαριθμούν από το 4 και μετά ή θα δώσουν κατευθείαν το άθροισμα κάνοντας νοερούς υπολογισμούς. (νοερή αρίθμηση) Αυτή η αναπτυξιακή αλλαγή έγκειται στο ότι τώρα τα παιδιά κατανοούν πως ένα χ σύνολο αντικειμένων μπορούμε να το δεχθούμε ως μια μεγάλη μονάδα, η οποία αποτελεί επαρκή αναπαράσταση της τιμής ενός συνόλου, και η οποία μπορεί να συνδυαστεί με μια μικρότερη. Πλέον, όταν τα παιδιά έχουν περάσει στη χρήση της στρατηγικής της μερικής απαρίθμησης, ενισχύεται η ικανότητα τους στην επίλυση της προσθετικής σύνθεσης. Η εν λόγω ερευνητική ομάδα, στην έρευνα που πραγματοποίησε με παιδιά ηλικίας 5-6 σε ένα έργο καταστήματος με χρήματα, κατέληξε στο συμπέρασμα πως υπάρχει σχέση ανάμεσα στον αριθμό των σωστών δοκιμασιών στις οποίες χρησιμοποιήθηκε η στρατηγική της μερικής απαρίθμησης/ μνήμης και στην επίδοση σε δοκιμασίες της προσθετικής σύνθεσης. Συμπεραίνουμε, επομένως, πως όταν τα παιδιά προοδεύσουν στην πρόσθεση, επιστρατεύοντας τη στρατηγική της μερικής απαρίθμησης, τότε είναι σε θέση να δοκιμάσουν να επιλύσουν προβλήματα προσθετικής ανάλυσης, η οποία αποτελεί τη βάση του δεκαδικού συστήματος. Τέλος, η έννοια της πρόσθεσης είναι επίσης συνδεδεμένη με εκείνη της αρίθμησης από έναν αριθμό και μετά. Ειδικότερα, όταν τα παιδιά χρησιμοποιούν τη στρατηγική της μερικής απαρίθμησης, ουσιαστικά πραγματοποιούν μια αρίθμηση από την απόλυτη τιμή ενός αριθμού και μετά. Για παράδειγμα, αν έχουν 5 αντικείμενα τα οποία βρίσκονται σε ένα κουτί, χωρίς να τα βλέπουν και άλλα τρία ορατά, τα παιδιά θα αριθμήσουν μερικώς από το πέντε και μετά. Σύμφωνα με τις προσεγγίσεις του Resnick για να εκτελεστεί η πράξη της πρόσθεσης διαδραματίζονται 2 ψυχολογικοί μηχανισμοί μάθησης. Το σχήμα διαδοχής και το σχήμα μέρος-μέρος-όλο. (αναφέρεται στο Ζαχάρος, 2007)
Το σχήμα διαδοχής αφορά τη νοερή αναπαράσταση των αριθμών (1-10), χωρίς να συσχετίζονται τα σύμβολα των αριθμών με τις ποσότητες που αντιπροσωπεύει το καθένα. Πιο συγκεκριμένα, θα την χαρακτηρίζαμε ως μια νοητική αριθμητική γραμμή, με την οποία επιτυγχάνονται οι πράξεις της πρόσθεσης και της αφαίρεσης. Το δεύτερο σχήμα, μέρος-μέρος-όλο, αφορά την «ικανότητα νοητικής αναπαράστασης του αριθμού ως σύνθεσης επιμέρους ποσοτήτων με ποικίλους τρόπους» (Ζαχάρος, 2007, σελ. 240). Στο σχήμα αυτό υπάρχουν κάποιες συγκεκριμένες αρχές. Αρχικά, το αποτέλεσμα παραμένει το ίδιο. Γνωρίζοντας την ποσότητα του ενός μέρους, τίθεται πολλή εύκολη η εύρεση του δεύτερου μέρους. Τέλος, οι πιθανοί συνδυασμοί που μπορούν να προκύψουν σχετικά με τις ποσότητες του κάθε μέρους, με σκοπό να παραχθεί το αποτέλεσμα, είναι προκαθορισμένοι.
ΕΡΕΥΝΗΤΙΚΑ ΔΕΔΟΜΕΝΑ ΓΙΑ ΤΟ ΠΩΣ ΑΝΑΠΤΥΣΣΕΤΑΙ Η ΜΑΘΗΜΑΤΙΚΗ ΕΝΝΟΙΑ ΑΠΟ ΤΑ ΜΙΚΡΑ ΠΑΙΔΙΑ- ΔΥΣΚΟΛΙΕΣ ΤΩΝ ΠΑΙΔΙΩΝ: Η έρευνα της Κορνηλάκη (1994) επιχείρησε να εξετάσει τη σχέση μεταξύ της πρόσθεσης και της προσθετικής ανάλυσης, σε ένα έργο πρόσθεσης. Γνωρίζοντας τη δυσκολία των παιδιών να κάνουν πρόσθεση χωρίς να καταφύγουν στην στρατηγική της ολικής απαρίθμησης, προσπάθησε να εμποδίσει τη χρήση αυτής της στρατηγικής δίνοντας ένα μη ορατό προσθετέο. [τα παιδιά καλούνταν να προσθέσουν δυο συλλογές κερμάτων. Η πρώτη συλλογή ήταν μη ορατή και για τις ανάγκες χρησιμοποιήθηκε ένα πορτοφόλι, ενώ στη δεύτερη η ποσότητα των κερμάτων βρισκόταν μπροστά στο παιδί]. Η έρευνα επιβεβαίωσε τα αποτελέσματα της προαναφερθείσας έρευνας της Nunes, ότι δηλαδή υπάρχει σχέση μεταξύ πρόσθεσης και προσθετικής ανάλυσης καθώς επίσης όταν το παιδί επιτυγχάνει να λύσει πρόβλημα πρόσθεσης με μια ορατό προσθετέο, χρησιμοποιώντας συνεπώς τη στρατηγική της μερικής απαρίθμησης, τότε απόκτα εν μέρει την ικανότητα να επιλύει προβλήματα προσθετικής ανάλυσης. (Κορνηλάκη στο Nunes, σελ 128-129) Ακόμη, όταν τα παιδιά χρησιμοποιούν τον απόλυτη τιμή ενός αριθμού και μετρούσαν από κει και μετά, υπήρχαν σημαντικές ενδείξεις πως θα επιτύγχαναν και την προσθετική σύνθεση. Η έρευνα της Κορνηλάκη είναι σημαντική γιατί κατέδειξε εκτός από τις δυσκολίες των παιδιών στην επίλυση προβλημάτων πρόσθεσης και τις στρατηγικές που υιοθετούσαν τα ίδια για να φθάσουν στη λύση.
Δυσκολίες: Τα παιδιά δυσκολεύονται να κάνουν πρόσθεση χωρίς να καταφύγουν στην στρατηγική της ολικής απαρίθμησης. Τα παιδιά 5-6 δυσκολεύονται να επιλύσουν προβλήματα πρόσθεσης με μη ορατό προσθετέο. Δεν είναι αυτονόητο για τα παιδιά πως «η απόλυτη τιμή ενός αριθμού είναι επαρκή αναπαράσταση του συνόλου και έτσι δεν είναι σε θέση να προσθέτουν σε αυτό ένα άλλο σύνολο». Χρειάζεται επομένως να απαριθμήσουν τα αντικείμενα της συλλογής ένα προς ένα ξανά.

Στρατηγικές: Τα παιδιά αναπαριστούσαν το μη ορατό προσθετέο με τα δάκτυλά τους ή μέσω άλλων χειρονομιών , αρχίζοντας από το ένα έως τη τιμή του προσθετέου. Αναπαριστούσαν τις μη ορατές μονάδες με λέξεις, είτε λέγοντας τις αριθμολέξεις γρήγορα, αριθμώντας έπειτα εκείνες που έβλεπαν, είτε έλεγαν τον απόλυτο αριθμό του προσθετέο και απαριθμούσαν στην συνέχεια τις ορατές μονάδες. Υπήρχε και ένα πολύ μικρό ποσοστό παιδιών που έδινε το άθροισμα των προσθετέων κατευθείαν, με νοητικές πράξεις.

ΕΠΙΛΟΓΗ ΛΟΓΙΣΜΙΚΩΝ ΓΙΑ ΤΙΣ ΜΑΘΗΣΙΑΚΕΣ ΔΡΑΣΤΗΡΙΟΤΗΤΕΣ

Επιλέξαμε τα λογισμικά Kidspiration και Virtual manipulatives, καθώς και τα δυο είναι κατάλληλα για παιδιά ηλικίας 3 ετών έως και 10 ετών και κατάλληλα για την κατανόηση της έννοιας της πρόσθεσης, λόγω των δυνατοτήτων που μας παρέχουν. Οι δυνατότητες αυτές αναλύονται παρακάτω.

Σκοπός και στόχοι του σεναρίου- σχεδίου διδασκαλίας

Γενικός σκοπός:

Οι μαθητές να μάθουν σταδιακά να προσθέτουν δυο αριθμούς, ξεκινώντας από απλά προβλήματα πρόσθεσης με ορατές συλλογές αντικειμένων και με ζητούμενο το άθροισμα και περνώντας σε πιο σύνθετα προβλήματα με άγνωστο προσθετέο ή με μη ορατό προσθετέο ή με προσθετέους υπό τη μορφή αφαιρετικών (κύβοι) ή αριθμητικών συμβολών. Επιπλέον, τα παιδιά μαθαίνουν μέσω μιας δραστηριότητες τους διαφορετικούς συνδυασμούς που υπάρχουν ώστε να προκύψει ο αριθμός έξι που σύμφωνα με τον Van de Walle μπορούν να τον μετρήσουν τα νήπια ήδη από την αρχή της χρονιάς, καθώς ε συνδυασμούς.(Van de Walle, 2007). Αργότερα επιλύουν προβλήματα στα οποία πρέπει να διερευνήσουν συνδυασμούς που δίνουν το άθροισμα ενός αριθμού που ζητάμε κάθε φορά.

Επιμέρους στόχοι δραστηριοτήτων:

Δ1) Να αναδειχθούν/ εντοπιστούν στρατηγικές αρίθμησης που ακολουθούν τα παιδιά για την πρόσθεση. Να απαριθμήσουν τα ψάρια από τις δύο γυάλες αναγράφοντας το άθροισμα τους.

Δ2) Να απαριθμήσουν τα φρούτα από τα δύο καλάθια αναγράφοντας το άθροισμα τους, ώστε να αντιληφθούν ότι το κάθε καλάθι αποτελεί ένα μέρος και το σύνολο και των δύο καλαθιών το όλο.

Δ3) 1. Να αντιληφθούν τα παιδιά πόσα ψάρια πρέπει να βάλουν ακόμη στην κενή γυάλα, ώστε να προκύψει το άθροισμα που δίνεται.

2. Να αντιληφθούν τα βήματα που πρέπει να μετατοπιστούν πάνω στην αριθμογραμμή προκειμένου να καταλήξουν στο άθροισμα που τους δίνεται.

Δ4)- Δ5) Να βρούν το άθροισμα των προσθετέων είτε κάνοντας μερική απαρίθμηση είτε προσθέτοντας νοερά.

Δ6) Να κατανοήσουν ότι ένας αριθμός μπορεί να αναλυθεί σε δύο μικρότερους αριθμούς, από το άθροισμα των οποίων μπορεί να προκύπτει και να διαπιστώσουν ότι κάθε αριθμός μπορεί να δημιουργηθεί από συγκεκριμένους συνδυασμούς δύο μερών.

Δ7) Να αναπαραστήσουν το πλήθος του αριθμού που δίνεται με κύβους και να επιχειρήσουν να αναλύσουν το πλήθος του σε μικρότερα σύνολα, ανακαλύπτοντας ένα πιθανό συνδυασμό δύο μερών που δίνει τον αριθμό.

Δ8) Να εκτελέσουν την μαθηματική πράξη που εμφανίζεται κάθε φορά ώστε να αντιληφθούν ότι η αφαίρεση είναι μια μορφή πρόσθεσης.

Προτεινόμενη εκπαιδευτική μέθοδος

Εκπαιδευτική μέθοδος: Ομαδοσυνεργατική και καθοδηγητική μάθηση, παρατήρηση, συζήτηση/ διάλογος

Τεχνικές:

Ερωτήσεις- απαντήσεις

Παιχνίδι δομημένο

Ομαδική εργασία

Υλικά:

Η/Υ

Λογισμικά kidspiration, Virtual manipulatives

Αριθμός παιδιών της τάξης και ηλικία παιδιών

Ο αριθμός των παιδιών είναι 10, ηλικίας 4 έως 6.

Εκτιμώμενη διάρκεια

Το σχέδιο θα πραγματοποιηθεί σε τρεις μέρες, αφού το περιεχόμενο του σεναρίου απαιτεί χρόνο για σταδιακή κατανόηση της έννοιας από τα παιδιά, ενώ ακόμη το ενδιαφέρον των παιδιών αμβλύνεται όταν μια δραστηριότητα διαρκεί πολύ. Κάθε μέρα μπορεί να αφιερώνονται 40 λεπτά για την πραγματοποίηση των προγραμματισμένων δραστηριοτήτων.

1η μέρα: δραστηριότητες 1, 2, 3

2η μέρα: δραστηριότητες 4, 5, 6

3η μέρα: δραστηριότητες 7, 8 και δραστηριότητα αξιολόγησης

ΑΝΑΠΤΥΞΗ ΣΕΝΑΡΙΟΥ- ΣΧΕΔΙΟΥ ΔΙΔΑΣΚΑΛΙΑΣ

Γενική περιγραφή

Η πρόσθεση

Σύμφωνα με τον Van de Walle η πρόσθεση χρησιμοποιείται για να κατονομαστεί το όλο σε σχέση με τα μέρη όταν αυτά είναι γνωστά. Υπάρχουν προβλήματα σύζευξης, μέρους-μέρους-όλου, διαχωρισμού και σύγκρισης, ωστόσο εμείς θα ασχοληθούμε στις δραστηριότητες μας με τους δύο πρώτους τύπους προβλημάτων.

Βασικός στόχος του διδακτικού σχεδίου είναι η κατανόηση της πρόσθεσης και μετά στην οποία ενσωματώνονται έξι συστατικά:

• Προφορική ονομασία αριθμών

• Γραπτή ονομασία αριθμών

• Το σχήμα Μέρος- μέρος- όλο

• Εγκατάλειψη στρατηγικής ολικής απαρίθμησης

• Στρατηγική της μερικής απαρίθμησης

• Το σχήμα διαδοχής

Προαπαιτούμενη Γνώση

Κατά την διδασκαλία του συγκεκριμένου σχεδίου διδασκαλίας οι μαθητές αναμένεται να είναι:

• Εξοικειωμένοι με τα αριθμητικά σύμβολα

• Εξοικειωμένοι με την άμεση αναγνώριση ποσοτήτων

• Εξοικειωμένοι με την καταμέτρηση ποσοτήτων

​ΑΦΟΡΜΗΣΗ

Η νηπιαγωγός μαζεύει τα νήπια στην γωνιά της παρεούλας προκειμένου να τους μιλήσει για το ενυδρείο που αγόρασε για την τάξη τους. Τους εμφάνισε το ενυδρείο και τους πρότεινε να το γεμίσουν με ψαράκια που θα φέρνουν κατά τη διάρκεια της χρονιάς με σκοπό να καταγράφουν κάθε μήνα σε ένα διάγραμμα το σύνολο των ψαριών που θα περιέχει το ενυδρείο. (Η καταγραφή αυτή θα διαρκέσει ολόκληρη την σχολική χρονιά ώστε τα παιδιά να βρίσκονται σε συνεχή επαφή με την πρόσθεση αλλά και να αναπτύξουν διάφορες δεξιότητες όπως παρατήρηση, μέτρηση, ερμηνεία παρατηρήσεων κ.α.). Αφού τα παιδιά έχουν δει και περιεργαστεί το ενυδρείο τοποθετούν μέσα σε αυτό δύο ψαράκια που έφερε η νηπιαγωγός. Έχοντας κάνει αυτή την εισαγωγή μεταφέρονται στην γωνιά της πληροφορικής με σκοπό να εργαστούν ομαδικά για να κάνουν τις παρακάτω δραστηριότητες.

Περιγραφή δραστηριοτήτων:

Δραστηριότητα 1^η

Η δραστηριότητα αυτή με τα ψάρια αποτελεί ένα πρόβλημα σύζευξης με άγνωστο το αποτέλεσμα. Γενικότερα στην πράξη της σύζευξης περιλαμβάνονται τρείς ποσότητες: ένα αρχικό ποσό, ένα ποσό αλλαγής (το μέρος που προστίθεται ή ενώνεται) και το τελικό ποσό (το αποτέλεσμα). Συγκεκριμένα στην εν λόγω δραστηριότητα υπάρχει ένα αρχικό ποσό και ένα ποσό αλλαγής και τα παιδιά καλούνται να βρουν το τελικό αποτέλεσμα. Τα παιδιά πρέπει να μετρήσουν τα ψάρια και από τις δύο γυάλες και να γράψουν το σύνολό τους στην τρίτη π.χ 3 ψάρια στην πρώτη γυάλα + 2 στην δεύτερη = 5 ψάρια στο σύνολο. Πρόκειται για μία δραστηριότητα χωρίς ιδιαίτερο βαθμό δυσκολίας, προκειμένου τα παιδιά να εισαχθούν στην έννοια της πρόσθεσης.

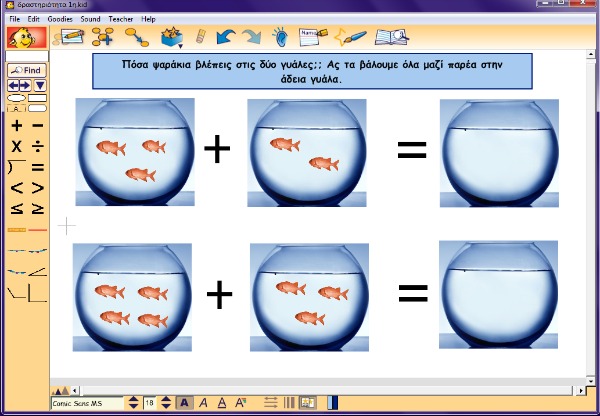
Ενδεικτικές ερωτήσεις

• Πόσα ψάρια βλέπετε στην πρώτη γυάλα;

• Πόσα ψάρια βλέπετε στην δεύτερη γυάλα;

• Ποια γυάλα έχει τα περισσότερα ψαράκια;

• Αν τα βάλουμε όλα μαζί στην τρίτη γυάλα πόσα θα έχουμε;

• Πως καταλήξατε στο αποτέλεσμα αυτό;

Δραστηριότητα 2^η

Η παραπάνω δραστηριότητα σχεδιάστηκε με βάση τη θεωρία Μέρος-μέρος-όλο. «Η θεωρία αυτή περιλαμβάνει δύο μέρη τα οποία συνδυάζονται και συγκροτούν ένα σύνολο. Ο συνδυασμός μπορεί να είναι μια φυσική πράξη ή να πραγματοποιηθεί νοερά με τα μέρη να μην συνδυάζονται στην πράξη». (Van de Walle, 2007, σελ 207) Στη δραστηριότητα αυτή είναι φανεροί και οι δύο προσθετέοι και λείπει το άθροισμα. Τα νήπια καλούνται να μετρήσουν πόσες φράουλες έχει το πρώτο καλάθι και πόσα πορτοκάλια το δεύτερο και να βρούν το σύνολο των φρούτων, π.χ: 3 φράουλες +2 πορτοκάλια = 5 φρούτα. Το ίδιο ισχύει και για τα υπόλοιπα καλάθια.

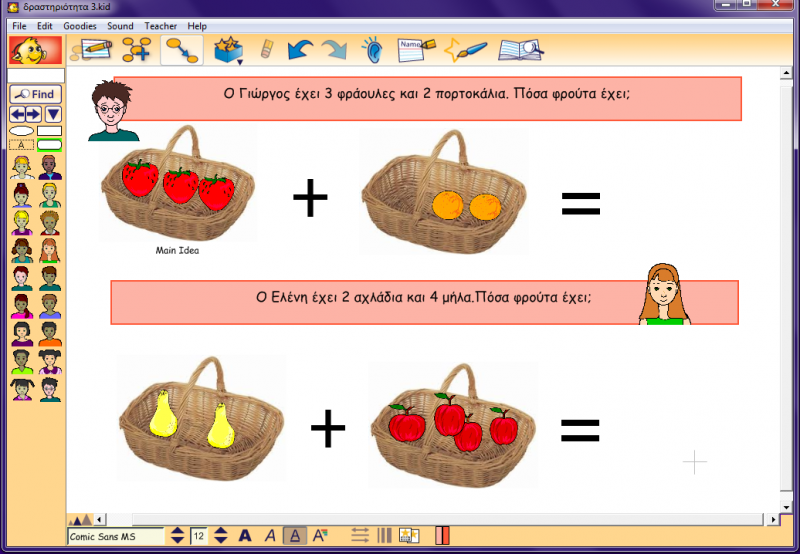
Ενδεικτικές ερωτήσεις

• Πόσες φράουλες έχει ο Γιώργος στο πρώτο καλάθι;

• Πόσα πορτοκάλια έχει ο Γιώργος στο δεύτερο καλάθι;

• Τώρα ο Γιώργος θέλησε να βάλει όλα τα φρούτα μαζί σ’ ένα καλάθι, για να μην κρατάει δύο καλάθια. Πόσα θα είναι όλα μαζί;

Δραστηριότητα 3^η

Στη τρίτη δραστηριότητα έχουμε ένα πρόβλημα σύζευξης με άγνωστο ένα εκ των δύο προσθετέων κάθε φορά. Τα παιδιά ουσιαστικά κάνουν μια μορφή αφαίρεσης καθώς πρέπει να δούνε το σύνολο των ψαριών της τρίτης γυάλας και να μοιράσουν τα ψάρια κατάλληλα ώστε να βγαίνει το επιθυμητό αποτέλεσμα. Πιο συγκεκριμένα, στο πρώτο παράδειγμα της δραστηριότητας, λείπει ο δεύτερος προσθετέος, επομένως τα παιδιά πρέπει να σκεφτούν πως αφού έχουμε στην πρώτη γυάλα 1 ψάρι και συνολικά 3 ψάρια, μας λείπουν 2 στη δεύτερη γυάλα.

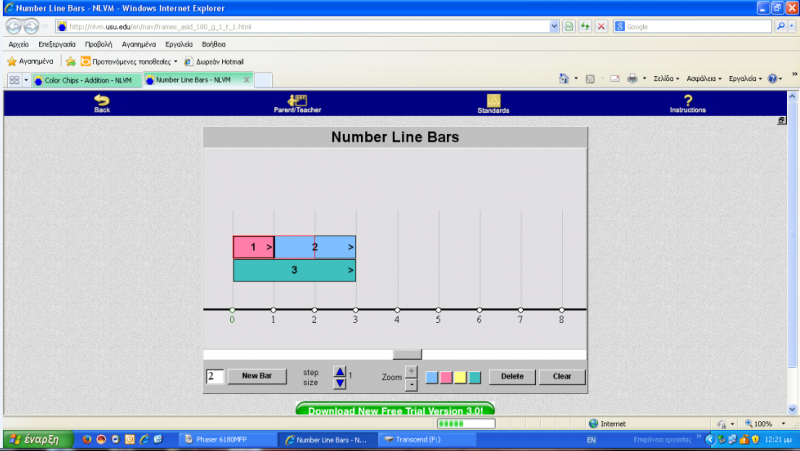
Την τρίτη αυτή δραστηριότητα μπορεί να συνοδεύει και η δραστηριότητα Number line bars από τα VM. Πιο συγκεκριμένα, τα παιδιά επειδή δυσκολεύονται περισσότερο σε προβλήματα που ο ένας προσθετέος είναι άγνωστος, θα ήταν πολύ χρήσιμη και βοηθητική η ύπαρξη μιας αριθμογραμμής (όπως αυτή που προσφέρει η εν λόγω δραστηριότητα των VM), η οποία θα αναπαριστά τα βήματα που μετατοπιζόμαστε όταν προσθέτουμε. Ειδικότερα, δίνεται η δυνατότητα τα νήπια να επιλέγουν μια μπάρα από το κουμπί "New bar", η οποία παίρνει τη τιμή που της δίνουν. Για παράδειγμα, αν το σύνολο των ψαριών είναι 3, τα νήπια μπορούν να πάρουν μια μπάρα που μετατοπίζεται 3 βήματα πάνω στην αριθμογραμμή, ενώ πάνω στην ίδια τη μπάρα αναγράφεται ο αριθμός των βημάτων. Στη συνέχεια, αναπαριστούν με μια μπάρα τον γνωστό προσθετέο και έτσι έχουν οπτικοποιημένη τη πράξη, ενώ παράλληλα αντιλαμβάνονται το μέρος- μέρος- όλο και τη σύνθεση ενός αριθμού. Δηλαδή, το όλο είναι 3 ψάρια και αποτελείται από τα μέρη 1 και 2.(αντίστοιχα ο αριθμός 3 συντίθεται από τους αριθμούς 2 και 1). Επιπλέον, προσφέρεται η δυνατότητα να χρωματίζεται διαφορετικά η κάθε μπάρα, ώστε να είναι διακριτά τα μέρη της πρόσθεσης. Τέλος, σύροντας το βέλος που υπάρχει στο τελείωμα της μπάρας 1 έως το τέλος της μπάρας 2, πραγματοποιείται αυτόματα η πρόσθεση και προκύπτει μια μπάρα με το άθροισμά τους.

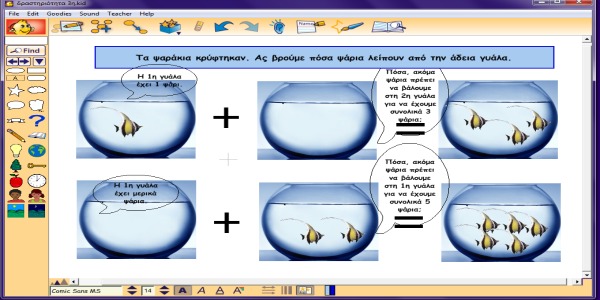
Ενδεικτικές ερωτήσεις

• Πόσα ψάρια βλέπετε στην πρώτη γυάλα;

• Η τελευταία γυάλα έχει το ένα ψαράκι της πρώτης γυάλας και τα ψαράκια που κρύφτηκαν από την δεύτερη. Πόσα ψαράκια έχει η τελευταία γυάλα;

• Αφού η πρώτη γυάλα έχει ένα ψαράκι, πόσα ακόμη ψαράκια χρειάζεται να βάλουμε στην δεύτερη γυάλα για να έχουμε συνολικά τρία;

• Ας πάμε σε ένα άλλο παιχνίδι. Ποιος θα μου περιγράψει τι βλέπει στην οθόνη του υπολογιστή; (Καθοδηγούμε τα παιδιά να στρέψουν την προσοχή τους στην αριθμογραμμή, στο κενό πλαίσιο για τον αριθμό δημιουργίας μπάρας, στα χρώματα, και το όλο περιβάλλον. Ζητάμε να κάνουν υποθέσεις για τη χρησιμότητας τους)

• Ποιο παιδάκι θα γράψει στο κουτάκι τον αριθμό των ψαριών της πρώτης γυάλας;

• Τι δημιουργήθηκε τώρα;

• Ας βάλουμε το κουτί που φτιάξαμε πάνω στην αριθμογραμμή. Πόσα βηματάκια έκανε πάνω σε αυτή;

• Πόσα ακόμη βήματα πρέπει να κάνουμε για να φτάσουμε τον αριθμό 3;

(συνεχίζουμε με ερωτήσεις τέτοιου τύπου)

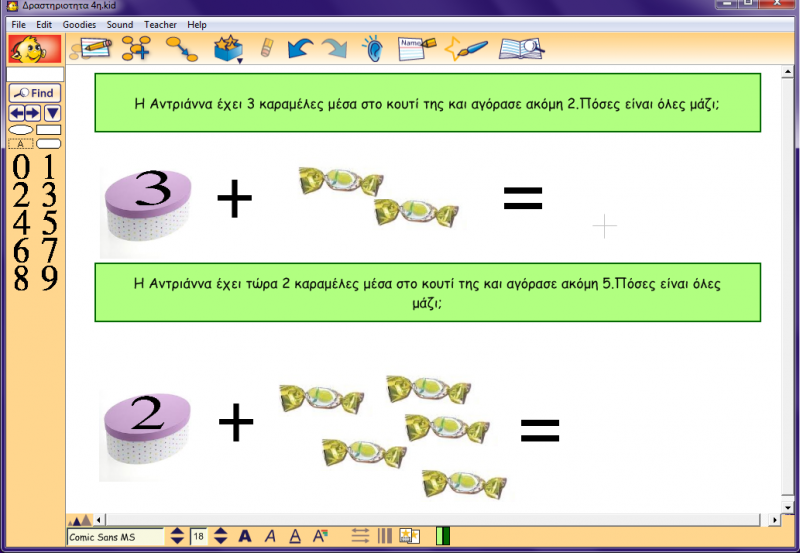
Δραστηριότητα 4^η -5^η

Αφού προηγήθηκαν οι παραπάνω δραστηριότητες πρόσθεσης με ορατούς προσθετέους, τα νήπια καλούνται να βρούν αθροίσματα σε πράξεις που υπάρχει μη ορατός προσθετέος, και ο οποίος ιδανικά θα ενισχύσει τη χρήση της στρατηγικής της μερικής απαρίθμησης. Ενδέχεται κάποια παιδιά να δώσουν κατευθείαν το άθροισμα κάνοντας νοερούς υπολογισμούς (νοερή αρίθμηση), ενώ κάποια άλλα ίσως να έχουν την ανάγκη να αναπαραστήσουν τον προσθετέο με τα δάκτυλά τους. Στην εν λόγω δραστηριότητα, θα πρέπει να βρουν το σύνολο των αντικειμένων μέσα στο κουτί/ κασετίνα (μη ορατοί προσθετέοι) και εκείνων έξω από αυτά.

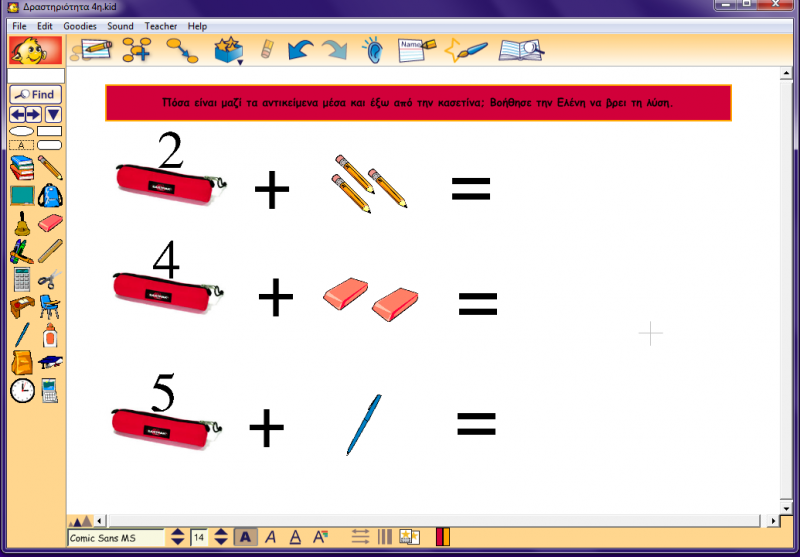
Ενδεικτικές ερωτήσεις

• Πόσα μολύβια βλέπετε να υπάρχουν έξω από την κασετίνα;

• Πόσα είναι όλα μαζί, μέσα και έξω από την κασετίνα;

• Πως καταλήξατε στο αποτέλεσμα αυτό;

Δραστηριότητα 6^η

Στην προκείμενη δραστηριότητα τα νήπια καλούνται να μετρήσουν πόσα μήλα βρίσκονται πάνω στο δέντρο και να γράψουν τον αριθμό στο κουτάκι του πρώτου προσθετέου καθώς επίσης να μετρήσουν πόσα μήλα περιέχει το καλάθι, αναγράφοντας τον αριθμό στο κουτάκι για το δεύτερο προσθετέο. Τέλος, πρέπει να βρουν το άθροισμα των δυο αριθμών από τα μήλα πάνω στο δέντρο και μέσα στο καλάθι. Σε όλες τις ασκήσεις της δραστηριότητας επιλέξαμε να βγαίνει ως άθροισμα ο αριθμός 6, ενώ η βασική μας επιδίωξη είναι να αντιληφθούν τα παιδιά μέσω των καθοδηγητικών μας ερωτήσεων τους διαφορετικούς τρόπους που ο αριθμός 6 μπορεί να αναλυθεί καθώς και να αναγνωρίσουν τα διαφορετικά ζεύγη των αριθμών που αν τα προσθέσουμε μας δίνουν τον αριθμό έξι. Πρόκειται για μια δραστηριότητα προσθετικής σύνθεσης/ ανάλυσης, στην οποία επιλέχθηκε ο αριθμός 6 διότι σύμφωνα με τον Van de Walle τα παιδιά τον αριθμό αυτό μπορούν να το μετρήσουν από την αρχή της χρονιάς.

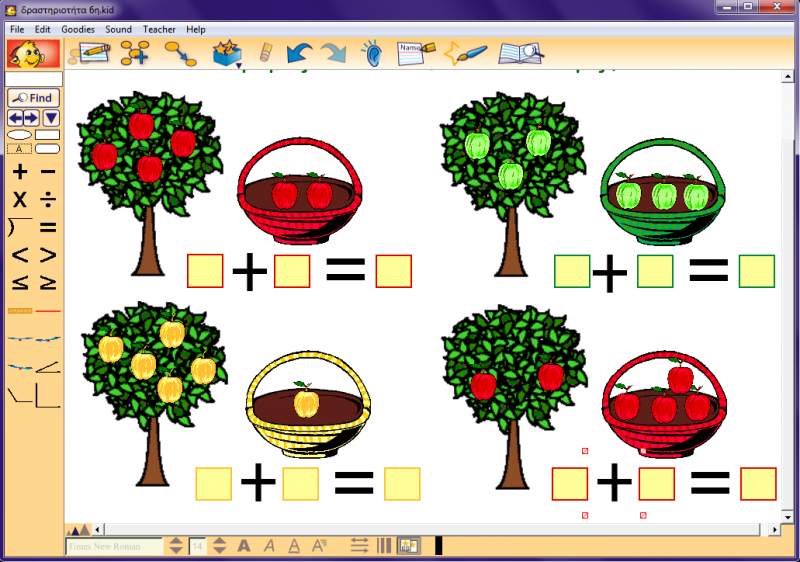
Ενδεικτικές ερωτήσεις

• Ποιο παιδί θα μου περιγράψει τι βλέπει στην οθόνη;

• Πόσα είναι τα κόκκινα μήλα πάνω στο δέντρο; Γράψε τον αριθμό στο πρώτο κουτάκι.

• Πόσα είναι τα κόκκινα μήλα μέσα στο καλάθι; Γράψε τον αριθμό στο δεύτερο κουτάκι.

• Πόσα είναι όλα μαζί;

(αφού τεθούν αντίστοιχες ερωτήσεις για όλα τα δέντρα, θέτουμε ερωτήσεις που στοχεύουν να επικεντρώσουν τη προσοχή των παιδιών στους διαφορετικούς συνδυασμούς που μας δίνουν τον αριθμό 6)

• Τι κοινό παρατηρείτε στα αποτελέσματα;

• Με πόσους διαφορετικούς τρόπους μπορούμε να φτιάξουμε 6 ομάδες από μήλα;

Δραστηριότητα 7^η

Σε αυτή τη δραστηριότητα που επίσης αποσκοπεί στην εξάσκηση της προσθετικής σύνθεσης, τα παιδιά καλούνται να ανταποκριθούν σε ένα πιο δύσκολο εγχείρημα. Ο βαθμός δυσκολίας έγκειται σε δύο λόγους: αφ΄ ενός τα μετρήσιμα υλικά είναι πιο συμβολικής και αφαιρετικής μορφής (κύβοι) και αφ’ ετέρου θα πρέπει τα ίδια να σκεφτούν ένα τρόπο να χωρίσουν τον αριθμό (τη συλλογή των κύβων) σε δυο μικρότερους, το άθροισμα των οποίων θα τους δίνει αυτόν τον αριθμό. Επομένως, τους δίνεται ένας αριθμός, τον οποίο πρέπει να αναπαραστήσουν με τόσα τουβλάκια όσα χρειάζονται για να δηλωθεί το πλήθος του. Στη συνέχεια χωρίζουν τα κυβάκια σε δυο ομάδες, που ουσιαστικά είναι οι 2 προσθετέοι, αναγράφοντας τον αριθμό των κύβων κάθε ομάδας στα 2 κενά προκειμένου να συμπληρωθεί η αριθμητική πράξη που δίνεται κάθε φορά.

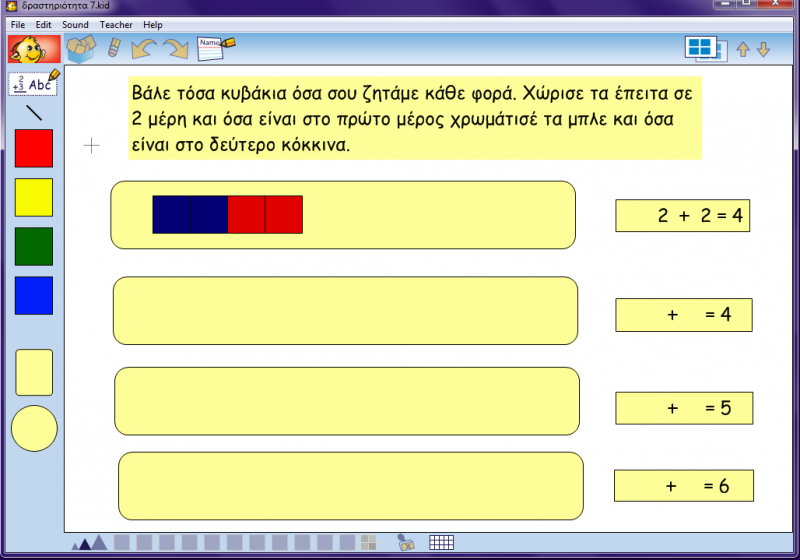Ενδεικτικές ερωτήσεις

• Ποιο παιδί θα μου περιγράψει τι βλέπει;

• Βάλτε τόσα κυβάκια όσα σας δείχνει ο αριθμός. Πόσα θα πρέπει να βάλετε μέσα στο πλαίσιο;

• Πως θα μπορούσαμε να χωρίσουμε τα κυβάκια σε δυο ομάδες;

• Πόσα θα βάζατε στη μια ομάδα και πόσα στην άλλη;

Δραστηριότητα 8^η

Η δραστηριότητα που επιλέξαμε στα VM είναι η Color Chips Addition καθώς έχουμε αναφέρει ότι η αφαίρεση είναι και μια μορφή πρόσθεσης. Αυτή η δραστηριότητα, όπως και οι υπόλοιπες που επιλέξαμε στο kidspiration εξοικειώνουν τα παιδιά με την έννοια της πρόσθεσης. Συγκεκριμένα στο πρώτο βήμα το παιδί καλείται να πατήσει πάνω στα σύμβολα ( + ) και ( – )και να τα σύρει μέσα στο κύκλο. Στο συγκεκριμένο παράδειγμα το παιδί πρέπει να σύρει τέσσερα συν και ένα πλην. Στην συνέχεια επιλέγει το πλήκτρο continue. Τώρα καλείται να πάρει ένα πλην και να το τοποθετήσει πάνω στο συν, ενώ αυτόματα αυτό εξαφανίζεται. Έτσι μένει στον κύκλο το αποτέλεσμα, δηλαδή το τρία. Τέλος το παιδί πρέπει να πληκτρολογήσει τον αριθμό που εκφράζει το πλήθος των συν που έχουν απομείνει στο κύκλο και το πρόγραμμα το ενημερώνει αν είναι σωστό το άθροισμα. Επιλέξαμε επομένως αυτό το πρόγραμμα διότι δίνει την δυνατότητα στο παιδί να μάθει αν το αποτέλεσμα της πράξης του είναι σωστό, ειδάλλως να ξανά μετρήσει τα συν για να καταλήξει στο ανάλογο άθροισμα. (δυνατότητα αποσφαλμάτωσης)

Αφού σχολιάσουμε και περιγράψουμε το περιβάλλον διεπαφής, θέτει η νηπιαγωγός ερωτήσεις σχετικές με τη δραστηριότητα.

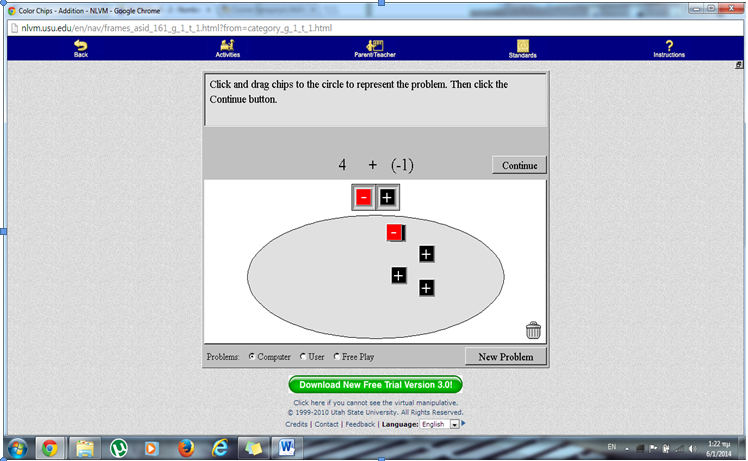
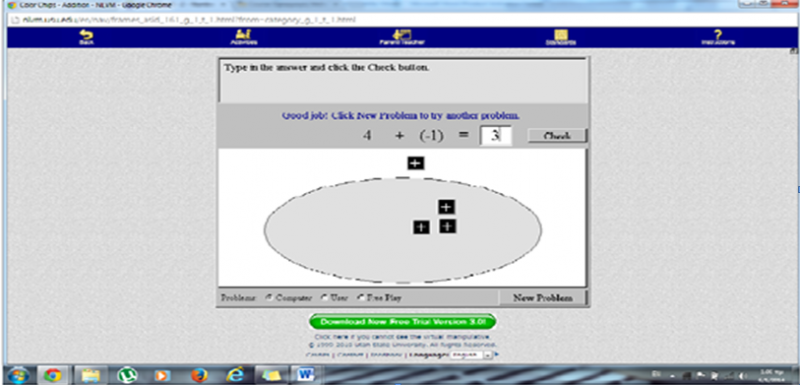Ενδεικτικές ερωτήσεις

• Ποιο παιδί αναγνωρίζει τα σύμβολα αυτά;

• Πόσα συν πρέπει να βάλουμε και πόσα πλην;

• Τώρα που εξαφανίστηκαν τα πλην πόσα συν έμειναν; Γράψτε τον αριθμό μέσα στο κουτί.

Αξιολόγηση:

Τα νήπια προκειμένου να αξιολογηθούν για τα όσα διδάχθηκαν καλούνται να δημιουργήσουν το δικό τους πρόβλημα πρόσθεσης στο περιβάλλον του kidspiration. Αυτό θα βοηθήσει τα παιδιά να εξωτερικεύσουν τις γνώσεις που αποκόμισαν και να αξιοποιήσουν τις δεξιότητες που ανέπτυξαν κατά την πραγματοποίηση των δραστηριοτήτων. Φυσικά, η νηπιαγωγός πάντα βοηθάει τα παιδιά στην προσπάθεια τους, αφού είναι ‘συνέταιρος’ με τα παιδιά στην οικοδόμηση της νέας γνώσης. Δημοσιοποιώντας τη γνώση τους τα παιδιά, υιοθετούν τρόπους έκφρασης και αναπαράστασης των ιδεών των παιδιών, μέσω της χρήσης κατάλληλων μέσων.

Αποτίμηση:

Από την παρούσα εργασία μας, αποκομίσαμε πολλά οφέλη. Αρχικά, εξοικειωθήκαμε με τα ψηφιακά λογισμικά Kidspiration και Virtual Manipulatives, καθώς λόγω της ενασχόλησης μας με αυτά, κερδίσαμε την εμπειρία σχεδιασμού μιας δραστηριότητας με τη βοήθεια νέας τεχνολογίας. Επιπλέον, μας δόθηκε η ευκαιρία να κάνουμε δραστηριότητες μαθηματικών για το νηπιαγωγείο, ώστε πρακτικά να δούμε πως οι έννοιες των μαθηματικών όπως η πρόσθεση μπορούν να διδαχθούν στα νήπια μέσα από δραστηριότητες που εμφανίζουν ενδιαφέρον για τα ίδια. Ακόμη, η ενασχόληση μας με τη βιβλιογραφία, μας βοήθησε στην πλήρη κατανόηση εννοιών των μαθηματικών καθώς επίσης εντοπίσαμε τις δυσκολίες που αντιμετωπίζουν τα παδιά στην προσπάθεια τους να κάνουν προσθέσεις. Αυτές τις δυσκολίες λάβαμε υπόψη στο σχεδιασμό των παραπάνω δραστηριοτήτων.