Διαίρεση
Submitted by zooulla92 on Sun, 06/16/2013 - 23:53
Μια διαδεδομένη άποψη σχετικά με την διαίρεση και τον πολλαπλασιασμό αφορά την αντίληψη ότι έπονται της πρόσθεσης και της αφαίρεσης, καθώς θεωρείται ότι δεν είναι απαραίτητο να γίνουν κάποιες σημαντικές διεργασίες για την κατανόηση τους από τα παιδιά μικρής ηλικίας. Ωστόσο, σύμφωνα με έρευνα και εκτεταμένη εξέταση του Piaget πάνω στο θέμα αποδεικνύεται το αντίθετο αφού σύμφωνα με τις μελέτες του είναι αναγκαίες ποιοτικές αλλαγές στον τρόπο σκέψης τους. Παρουσιάζονται ποικίλες διαφορές ανάμεσα στα ζεύγη του πολλαπλασιασμού-διαίρεσης και πρόσθεσης-αφαίρεσης. Για παράδειγμα, στον προσθετικό συλλογισμό απαιτούνται καθαρά οι πράξεις της ένωσης και του διαχωρισμού, σε αντίθεση με το δεύτερο ζεύγος όπου αυτές οι πράξεις εμπλουτίζονται και από άλλες γνώσεις. Έτσι, το παιδί καλείται να αφομοιώσει ένα νέο σχήμα νοημάτων του αριθμού και ένα σύνολο σταθερών τα οποία όμως αφορούν το ζεύγος του πολλαπλασιασμού και της διαίρεσης και απομακρύνονται από την πρόσθεση και την αφαίρεση.
Όσον αφορά τη διαίρεση, αυτή είναι γνωστή στο νηπιαγωγείο ως ‘’μοίρασμα’’. Το μοίρασμα αναφέρεται στην κατανομή ενός ολικού συνόλου μεταξύ ενός αριθμού αποδεκτού. Ένα κλασικό παράδειγμα που χρησιμοποιείται στο χώρο του νηπιαγωγείου-σχολείου είναι το εξής: Τρία παιδιά θα μοιραστούν εξίσου 24 καραμέλες που τους έδωσε η μητέρα τους. Πόσες καραμέλες θα πάρει το καθένα. Σχέσεις μέρους-όλου όπως στα προσθετικά προβλήματα όπου λαμβάνεται υπόψη το μέγεθος του όλου που είναι το άθροισμα των μερών, που δεν χρειάζεται να είναι ίσα λαμβάνουν χώρα και στη διαίρεση και στο μοίρασμα. Σε αυτό το ζεύγος όμως λαμβάνουμε υπόψη μας το μέγεθος του όλου, τον αριθμό των μερών αλλά και το μέγεθος των μερών το οποίο πρέπει να είναι ίδιο με όλα τα μέρη. Για παράδειγμα αν υπάρχουν 10 γλυκά (το όλον) και 5 παιδιά για να τα μοιραστούν (5 μέρη) ,υπάρχουν 2 γλύκα για κάθε παιδί (το μέγεθος του μέρους ή μερίδιο).Οπότε σε αυτό το σημείο τα παιδιά καλούνται να κατανοήσουν τρεις έννοιες. Εξηγώντας, αν διατηρήσουμε τον αριθμό των παιδιών ίδιο και αυξήσουμε τον αριθμό των γλυκών θα αντιστοιχούν περισσότερα γλυκά ανά παιδί. Αν όμως διατηρήσουμε τον αριθμό των παιδιών ίδιο και αυξήσουμε τον αριθμό των παιδιών θα αντιστοιχούν λιγότερα γλυκά ανά παιδί.
Επομένως υπάρχουν νέες σχέσεις οι οποίες προστίθενται σχετικά με το μοίρασμα και τους διαδοχικούς διαμερισμούς. Έτσι σύμφωνα και με τα αποτελέσματα των Correa-Bryant η κατανόηση εκ μέρους των παιδιών αυτής της σχέσης αποτελεί ένα βασικό βήμα πέρα από την δραστηριότητα του μοιράσματος σε αυτήν της διαίρεσης. Σύμφωνα με την Confrey ,όταν η διαίρεση εκτελείται διαδοχικά σε ένα σύνολο ή αντικείμενο, αυτές οι διαιρέσεις προκαλούν μια αλλαγή στη σχέση όλου-μερών. Σε αυτό το σημείο υπάρχει και ένα νέο μήνυμα του αριθμού που αναφέρεται στο ρυθμό αλλαγής, δηλαδή διαφέρει ο ρυθμός αλλαγής στον διαμερισμό σε δύο κομμάτια από αυτόν σε τρία.
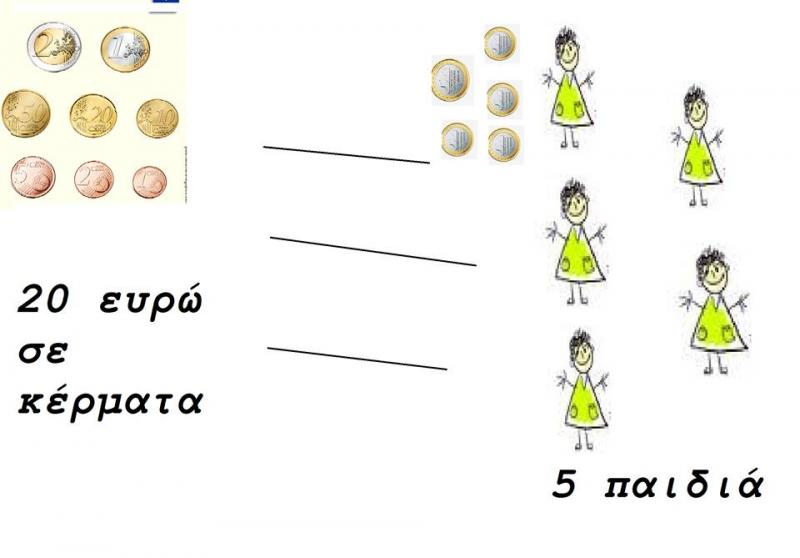
Συνοψίζοντας, το μοίρασμα αναφέρεται στην πράξη της διαίρεσης και με την πιθανότητα διαδοχικών διαμερισμών. Υπάρχουν κατηγορίες στις οποίες κατατάσσεται η διαίρεση και είναι οι εξής: 1. Προβλήματα διαίρεσης-μερισμού (χωρισμός μιας δεδομένης ποσότητας σε ίσα μέρη, όπως αναφέρθηκε παραπάνω) 2. Προβλήματα διαίρεσης-μέτρησης (δημιουργία ομάδων με τον ίδιο αριθμό στοιχείων). Παράδειγμα: Ο Γιάννης έχει 20ε και θέλει να αγοράσει σοκολάτες που κοστίζουν 2ε η μία. Πόσες σοκολάτες μπορεί να αγοράσει;
Παράγοντες που επηρεάζουν τη δυσκολία ενός προβλήματος πολλαπλασιασμού ή/και διαίρεσης:
Ο Fischbein αναφέρει ότι αναπτύσσονται ιδιαίτερα νοητικά μοντέλα προκειμένου τα παιδιά να κατανοήσουν μαθηματικές έννοιες και πράξεις στις οποίες παρουσιάζουν δυσκολία. Σύμφωνα με τις έρευνές του, τα μοντέλα αυτά χαρακτηρίζονται ως ιδιαίτερα ανθεκτικά και καλά στερεωμένα .Έτσι ανταποκρίνονται καλύτερα στις νοητικές απαιτήσεις των παιδιών. Σ’ αυτό το σημείο ο εκπαιδευτικός έρχεται σε ένα μεγάλο δίλημμα όπου θα πρέπει να αποφασίσει εάν θα συσχετίσει την επιστημονική γνώση με αυτά τα άτυπα μοντέλα για να επιτύχει την καλύτερη κατανόηση της από τους μαθητές ή αν θα πρέπει να αποφευχθεί ο παραλληλισμός με αυτά για να μην αποτελέσουν τελικά εμπόδιο στην ορθή επιστημονική γνώση. Ίσως μία κατάλληλη λύση θα ήταν να εμπλουτιστούν οι μαθητές με τέτοια εργαλεία ώστε να μπορούν να ελέγξουν τις πρωτογενείς τους γνώσεις. Επιπλέον, σε ένα πρόβλημα το οποίο περιέχει αριθμούς μεγαλύτερους του 100,είτε δεκαδικούς, είτε κλάσματα να παρουσιαστεί μεγαλύτερη δυσκολία κατανόησής τους. Ακόμα, η μορφή του τελεστή κλίμακας ή του συναρτησιακού τελεστή επηρεάζει σε πολύ μεγάλο βαθμό τη δυσκολία ενός προβλήματος. Η αντίληψη ότι "ο πολλαπλασιασμός μεγαλώνει" και "η διαίρεση μικραίνει" αποτελούν σοβαρά επιστημολογικά εμπόδια με την έννοια ότι οι δεκαδικοί τελεστές εμποδίζουν την κατανόηση του προβλήματος από τους μαθητές.
Άτυπες στρατηγικές αντιετώπισης προβλημάτων διαίρεσης:
Στην περίπτωση κατά την οποία οι μαθητές δεν κατανοούν το πότε ακριβώς διαιρούμε μη έχοντας μια συνειδητή προσέγγιση προς τον γραπτό αλγόριθμο, η διδασκαλία της διαίρεσης είναι μια γνώση χωρίς αποτέλεσμα παιδιά πριν διδαχθούν τη διαίρεση είναι σε θέση να αντιμετωπίσουν καταστάσεις διαμέρισης με τη χρήση πρόσθεσης, αφαίρεσης και πολλαπλασιασμού, ακόμα και μετά την εκμάθηση της διαίρεσης.
Τρεις κατηγορίες άτυπως στρατηγικών επίλυσης προβλημάτων διαίρεσης 1. Διαδικασία βήμα προς βήμα Σ αυτήν την κατηγορία τα παιδιά μεταφέρουν τις καταστάσεις του προβλήματος σε πραγματικές διαστάσεις και όχι σε μαθηματικά πλαίσια. Ωστόσο, συχνά αντιμετωπίζουν προβλήματα όπως δυσκολίες αποκωδικοποίησης αποτελέσματος αλλά και στην πορεία εγκαταλείπουν την προσπάθεια. 2. Κατασκευαστικές Διαδικασίες
Τα παιδιά κατασκευάζουν τον ζητούμενο αριθμό με σταθερά βήματα μέσω ενός συγκεκριμένου προγράμματος έχοντας υπόψη τα ενδιάμεσα αποτελέσματα. Διακρίνονται 6 κατηγορίες: α) Επαναλαμβανόμενες προσθέσεις του διαιρέτη, β)Επαναλαμβανόμενες προσθέσεις του διαιρέτη με σημείο κίνησης ένα πολλαπλάσιο του διαιρέτη, γ)Επαναλαμβανόμενες αφαιρέσεις του διαιρέτη, δ)Επαναλαμβανόμενες αφαιρέσεις του διαιρέτη με σημείο εκκίνησης ένα πολλαπλάσιο του διαιρέτη, ε)Επαναλαμβανόμενοι πολλαπλασιασμοί του διαιρέτη με αυθαίρετο αριθμό. Τρόποι αντιμετώπισης δυσκολιών και παρανοήσεων σχετικά με τη διαίρεση.
Οι Hiebert και Berh διατύπωσαν την άποψη ότι χρειάζεται να αναζητηθούν οι στρατηγικές διδασκαλίας που θα διευκόλυναν τα παιδιά να κατανοήσουν καλύτερα την κατασκευή του νοήματος των γραπτών μαθηματικών συμβόλων και να αναπτύξουν τις βασικές εννοιολογικές στρατηγικές από την πρώτη στιγμή της εμφάνισης τους μέχρι και τη στιγμή της μορφής τυπικών διαδικασιών. Ο δάσκαλος όμως για να βοηθήσει τους μαθητές του πρέπει να προβεί σε κάποιες ενέργειες: 1) Να εγκαταστήσει ένα πρόγραμμα επικοινωνίας που θα ισορροπεί τη άτυπη γλώσσα, 2)Να παρακινήσει τους μαθητές που δεν γνωρίζουν πώς να αντιμετωπίσουν την κατάσταση, ως μια πραγματική κατάσταση, 3) Να τους παροτρύνει να χρησιμοποιήσουν κατασκευαστική μέθοδο. Αυτή η διαδικασία περιλαμβάνει απόκτηση κάποιων ικανοτήτων όπως: α) Ικανότητα να λύνουν με το νου προβλήματα της ίδιας δομής με το δεδομένο, αλλά με μικρότερους αριθμούς, β) Ικανότητα να διατυπώνουν μια υπόθεση και να την ελέγχουν, γ) Ικανότητα διατύπωσης προσεγγιστικής απάντησης για τον έλεγχο της ορθότητας της αριθμητικής λύσης. Οι σημαντικότερες παρανοήσεις που παρατηρήθηκαν: 1. Λανθασμένη ερμηνεία του υπολοίπου, 2.Σύγχυση πηλίκου-υπολοίπου, 3.Σύγχυση μεταξύ εννοιών αφαίρεσης και διαίρεσης, 4.Σύγχυση μεταξύ πολλαπλασιασμού και διαίρεσης, 5.Λανθασμένη συσχέτιση γεωμετρικών- αριθμητικών γνώσεων
Ρεαλιστική προσέγγιση του πολλαπλασιασμού:
Η ρεαλιστική προσέγγιση είναι η ανάπτυξη του αλγόριθμου πολλαπλασιασμού με το φυσικό τρόπο σκέψης των παιδιών. Πραγματοποιείται σε τέσσερις φάσεις: 1. Την προαλγοριθμική φάση: που το πρόβλημα δεν παραπέμπει άμεσα στη πράξη του πολλαπλασιασμού. Τα παιδιά επιλέγουν το δικό τους τρόπο λύσης του προβλήματος. 2.Την φάση της αναγνώρισης της σχέσης μεταξύ της αξίας θέσης και της επαναλαμβανόμενης πρόσθεσης: όπου σε μια επιλεγμένη κατάσταση δίνεται έμφαση στις στρατηγικές των παιδιών που βρίσκεται στη διαδικασία του αλγορίθμου. Κάποια παιδιά για να λύσουν ένα πρόβλημα θα χρησιμοποιήσουν τις γνώσεις τους για το πολλαπλασιασμό ενώ κάποια άλλα με τις επαναλαμβανόμενες προσθέσεις. 3.Στη Τρίτη φάση είναι καθαρά τα αλγοριθμικά: Τα παιδιά θα δουλέψουν με την επανάληψη 4.Στη φάση της γενίκευσης τα παιδιά θα πρέπει να είναι ικανά να χρησιμοποιούν το πολλαπλασιασμό και όχι τις επαναλαμβανόμενες προσθέσεις και να βρίσκουν το αποτέλεσμα με σύντομες διαδικασίες.
Ρεαλιστική προσέγγιση της διαίρεσης:
Όπως και στον πολλαπλασιασμό, έτσι και εδώ με τη ρεαλιστική προσέγγιση της διαίρεσης τα παιδιά είναι ελεύθερα να διαλέξουν το δικό τους τρόπο λύσης προβλήματος. Ο K.Gravemeijer αναφέρει ότι σε μια διδασκαλία κάποιων μαθητών του δημοτικού που δεν είχαν κάνει πολλαπλασιασμό μεγαλύτερο του 10 και με αφορμή ένα πρόβλημα όπως « Τρία παιδιά θα μοιρασθούν 36 γλυκά. Πόσα θα πάρει το καθένα;» τα παιδιά αυθόρμητα ανάφεραν κάποιες λύσεις όπως: 1. «Γεωμετρικός» χωρισμός των γλυκών 2.Μοιρασιά ένα προς ένα. 3.Ομαδοποίηση 4.Η διαίρεση μερισμού 5. Η διαίρεση μέτρησης. Μέσα από αυτό παρατηρούμε ότι τα παιδιά εφαρμόζουν δύο διαδικασίες αυθόρμητα. Ο αλγόριθμος της διαίρεσης είναι μια διαδικασία υπολογισμού το πόσες φορές ο διαιρέτης μπορεί να αφαιρεθεί από το διαιρετέο. Επίσης η ρεαλιστική προσέγγιση ξεκινά από τα άτυπες μεθόδους των παιδιών ως βάση στήριξης των τυπικών μαθηματικών διαδικασιών.
Η πράξη της διαίρεσης είναι μία από αυτές που δεν είναι εύκολα αντιληπτές από τα παιδιά προσχολικής ηλικίας. Τα παιδιά συνδέουν συνήθως την διαίρεση με το μοίρασμα. Έχουμε το "όλο" το οποίο μοιράζεται σε επιμέρους τμήματα. Βέβαια για τα παιδιά της προσχολικής ηλικίας είναι πολύ σημαντικό να κατανοήσουν ότι ένα ενιαίο κομμάτι μπορεί να αναλυθεί σε μέρη ίσου μεγέθους. Στο νηπιαγωγείο τα νήπια χρησιμοποιούν διάφορες στρατηγικές για να μπορέσουν να κατανοήσουν και να αφομοιώσουν αυτήν την έννοια.Η πιο συνηθισμένη είναι αυτή της συνεχόμενης αφαίρεσης ή ομαδοποίησης. Δηλαδή "αν έχεις 6 καραμέλες σε πόσα παιδιά μπορείς να δώσεις από 2;". Σε κάθε περίπτωση, τα παιδιά θα πρέπει να ενθαρρύνονται στην ενασχόλησή τους με κάθε μαθηματική έννοια στην οποία παρουσιάζονται δυσκολίες, αλλά και γενικότερα στην δραστηριοποίησή τους με τα μαθηματικά και να τονίζεται κάθε φορά η σημασία τους για καθημερινές πρακτικές και από τους εκπαιδευτικούς αλλά και από τους γονείς.
Ως παιδαγωγικό υλικό μπορεί να χρησιμοποιηθεί: πλαστικά ψάρια, αγκίστρια ψαρέματος, κουβά, επιτραπέζιο, βότσαλα, κουβάδες, χάρτινους αριθμούς, κέρματα, λουλούδια.
Φύλλα εργασίας:
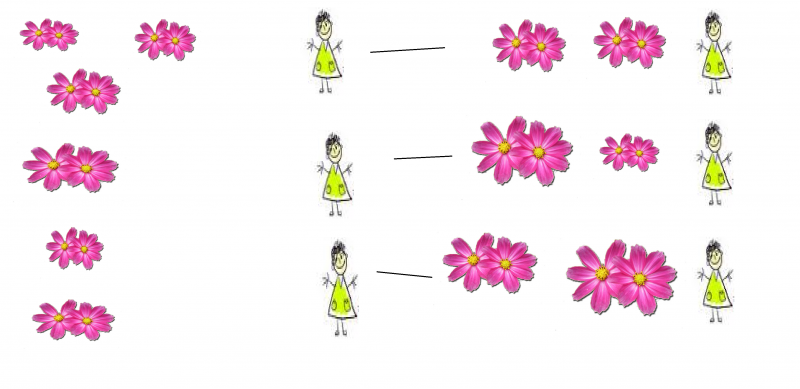

Δραστηριότητα Επέκτασης (με παιδιά με μαθησιακές δυσκολίες): Οργανώνονται στο σχολείο καλοκαιρινά παιχνίδια με σκοπό την έναρξη του καλοκαιριού και για την κινητοποίηση των παιδιών. Η νηπιαγωγός αρχικά κάνει συζήτηση με τους μαθητές προκειμένου να τους εισάγει στο θέμα του καλοκαιριού και των στοιχείων που το χαρακτηρίζουν. Χρησιμοποιούνται και κάποια καλοκαιρινά αντικείμενα τα οποία έχει φέρει η νηπιαγωγός στην τάξη. Οργανώνει διάφορα παιχνίδια σχετικά με το καλοκαίρι έξω στην αυλή του σχολείου έτσι ώστε τα παιδία να ενημερωθούν για το θέμα.
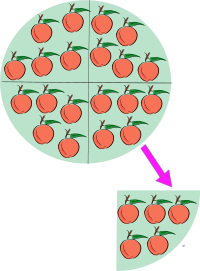
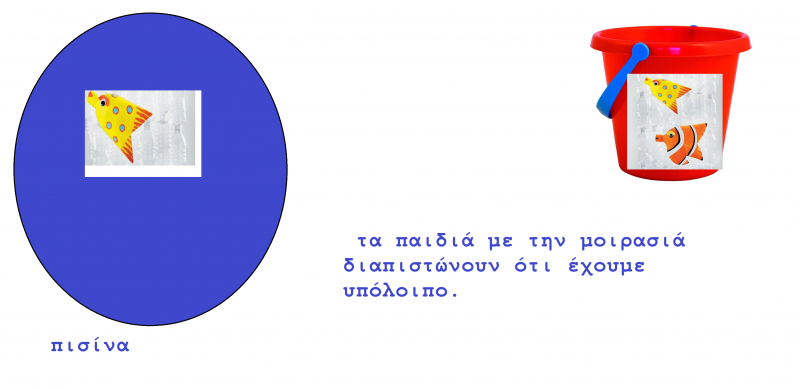
Τα παιδιά χωρίζονται σε διάφορες ομάδες ανάλογα με τις μαθησιακές τους δυσκολίες για να απασχοληθούν και να εξοικειωθούν με κάποιες έννοιες των μαθηματικών και σε ότι αφορά το καλοκαίρι. Αρχικά η μια ομάδα των παιδιών θα ασχοληθεί με το πρώτο παιχνίδι που περιέχει μία διαμορφωμένη πισίνα όπου τα παιδιά θα παίξουν ένα παιχνίδι ψαρέματος. Στο συγκεκριμένο παιχνίδι η νηπιαγωγός μοιράζει στον καθένα από ένα αγκίστρι αλλά και έχουν τοποθετηθεί μέσα στην πισίνα ψάρια διαφορετικού χρώματος και τα νήπια προσπαθούν να μαζέψουν όσα πιο πολλά ψάρια μπορούν. Μετέπειτα, αφού τα έχουν μαζέψει σε ένα κουβά τα μοιράζουν, και διαπιστώνουν ότι έχουν υπόλοιπο. Με τον τρόπο αυτό τα παιδιά μαθαίνουν ότι σε μια πράξη μπορεί να υπάρξει υπόλοιπο (δηλαδή πάντα μπορεί να μείνει κάποιο απ' έξω.)
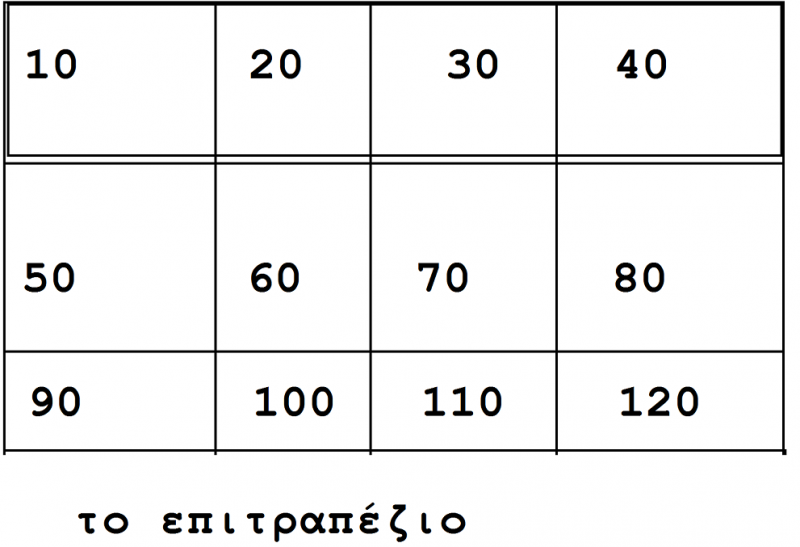
Επίσης, μια άλλη ομάδα παιδιών θα ασχοληθεί σε ένα άλλο παιχνίδι όπου είναι έτσι σχεδιασμένο για τις ανάγκες αυτής τις ομάδας παιδιών. Το παιχνίδι είναι ένα επιτραπέζιο το οποίο είναι χωρισμένο σε κουτιά στα οποία αναγράφονται αριθμοί 10, 20, 30……κτλ. Οι μαθητές καλούνται να ρίχνουν ένα βότσαλο και σε όποιο κουτί τύχει διαιρούν το 10 με τον αναγραφόμενο αριθμό. Για παράδειγμα, το βότσαλο πέφτει στο κουτί με το 40 τα παιδιά το διαιρούν με το 10, βρίσκουν το αποτέλεσμα και πρέπει να αναφέρουν 4 στοιχεία της θάλασσας και του καλοκαιριού.
Η τρίτη ομάδα παίζει ένα παιχνίδι όπου υπάρχουν πέντε ( 5) κουβάδες και είκοσι (20) ψάρια έξω από αυτούς. Η νηπιαγωγός χωρίζει τα παιδιά σε δύο ομάδες. Κάθε φορά φωνάζει διαφορετικές πράξεις ( δηλ. 6/3 κλπ.) όπου πρέπει τα παιδιά να βρουν το αποτέλεσμα και να μοιράσουν τα ψάρια στους κουβάδες. Σε αυτό το σημείο έχουμε αναφέρει στα παιδιά ότι τα ψάρια είναι ο διαιρετέος και οι κουβάδες ο διαιρέτης.
Η τελευταία ομάδα των παιδιών πρόκειται να απασχοληθούν με ένα κινητικό παιχνίδι όπου η νηπιαγωγός έχει μοιράσει διάφορους αριθμούς στα παιδιά για να τα φορέσουν στην μπλούζα τους. Τα παιδιά βλέπουν τον αριθμό της μπλούζας τους και ψάχνουν το συμμαθητή που έχει το μισό τους. Για παράδειγμα, το παιδί που έχει τον αριθμό 20 προσπαθεί να βρει το παιδί με τον αριθμό 10.
Τέλος η νηπιαγωγός δημιούργησε μια δραστηριότητα έτσι ώστε να καλύψει τις διάφορες μαθησιακές ανάγκες του κάθε παιδιού. Με αυτό τον τρόπο τα παιδιά είχαν ένα κοινό θέμα το καλοκαίρι αλλά και ένα ξεχωριστό αποτέλεσμα το οποίο βασίστηκε στις μαθησιακές τους ανάγκες. Επιπλέον, στο τέλος των δραστηριοτήτων κάθε ομάδα παρουσιάζει στα υπόλοιπα παιδιά τι έκανε στο δικό της παιχνίδι και γίνεται μία συζήτηση σχετικά με τις δραστηριότητες και τις μαθηματικές έννοιες.
Ζαχάρος, Κ. (2007). Οι μαθηματικές έννοιες στην προσχολική εκπαίδευση και η διδασκαλία τους. Επιστήμες της Αγωγής · Διδακτική - Αναλυτικά Προγράμματα - Αξιολόγηση. Β. Βασιλού - Παπαγεωργίου (Επιμελ. Σειράς). Αθήνα : Μεταίχμιο
Κολέζα, Ε. Γ. (2000). Γνωσιολογική και διδακτική προσέγγιση των στοιχειωδών μαθηματικών εννοιών. Επιστημολογία και Διδακτική των Μαθηματικών και Φυσικών Επιστημών. Αθήνα : Leader Books
Τζεκάκη, Μ. (2007) Μικρά παιδιά, μεγάλα μαθηματικά νοήματα : Προσχολική και πρώτη σχολική ηλικία. Παιδαγωγική Σειρά. Αθήνα : Gutenberg - Γιώργος & Κώστας Δαρδανός Montague -
Smith, A. (2007). Μαθαίνω τη διαίρεση. Παιδική Βιβλιοθήκη · Η Λέσχη των Αριθμών. Έ. Χριστοπούλου (Μεταφρ.)., Σπυρίδων Κονταράκης (εικονογράφηση). Αθήνα : Εκδοτικός Οίκος Α. Α. Λιβάνη
Nunes, T., Bryant, P. (2007) Τα παιδιά κάνουν μαθηματικά. επιμέλεια Δ. Δεσλή (Επιμέλ.). Σ. Λειβαδοπούλου, Γεωργία Σαρηγιαννίδου (Μεταφρ.). Σ. Βοσνιάδου (Επιμελ. Σειράς). Αθήνα : Gutenberg - Γιώργος & Κώστας Δαρδανός