Κατανόηση ισότητας και ομοιότητας σχημάτων
Submitted by kerestet on Sun, 06/16/2013 - 20:24Η εργασία αυτή έχει ως θέμα την " Κατανόηση ισότητας και ομοιότητας σχημάτων". Μέσα από αυτή την εργασία είχαμε την δυνατότητα να έρθουμε σε επαφή με ένα μέρος των μαθηματικών εννοιών. Στην εργασία αυτή θα παρουσιάσουμε τους ορισμούς των γεωμετρικών σχημάτων, της συμμετρίας καθώς και τους ορισμούς της ισότητας και ομοιότητας των σχημάτων. Στη συνέχεια, παρουσιάζουμε κάποια παιδαγωγικά υλικά, που μπορούν να χρησιμοποιηθούν για την κατανόηση αυτού του θέματος. Επίσης, θα παρουσιάσουμε κάποιες δραστηριότητες που προτείνουν οι ειδικοί σχετικά με αυτό το θέμα. Τέλος, θα παρουσιάσουμε μια ενδεικτική δραστηριότητα σχετικά με αυτό το θέμα.

Τα γεωμετρικά σχήματα, σύμφωνα με τον E. Fischbein, είναι νοητικές οντότητες, οι οποίες έχουν δυο τύπους χαρακτηριστικών την εννοιολογική και την σχηματική φύση. Με αυτή τη λογική παίρνουμε, για παράδειγμα, μια σφαίρα. Η σφαίρα ως προς την εννοιολογική της φύση είναι μια αφηρημένη, ιδεατή αλλά και τυπικά καθορισμένη οντότητα, όπως και κάθε άλλη έννοια. Επιπλέον, ως προς την σχηματική της φύση, εννοούμε τις διάφορες σχηματικές ιδιότητες, που έχει, το συγκεκριμένο σχήμα, δηλαδή, που την χαρακτηρίζει. Στη συνέχεια, η έννοια του γεωμετρικού σχήματος, ως προς το θεωρητικό παίσιο, περιλαμβάνει τρεις ενότητες: τον ορισμό, την εικόνα, η οποία στηρίζεται στην αισθησιο-αντηλιπτική εμπειρία και την σχηματική έννοια. Ο Fischbein υποστηρίζει ότι το γεωμετρικό σχήμα είναι μια γραφική συγκεκριμένη, υλική παρουσίασή του. Πρόκειται, δηλαδή, για την ιδέα που αντιστοιχεί στο σχέδιο. Είναι η αφηρημένη, ιδεατή οντότητα, που καθορίζεται πλήρως από τον ορισμό.
Ένα σημαντικό χαρακτηριστικό που συναντούμε στα γεωμετρικά σχήματα είναι η ομοιότητα και η ισότητα, που υπάρχει μεταξύ τους.
Ισότητα σχημάτων:
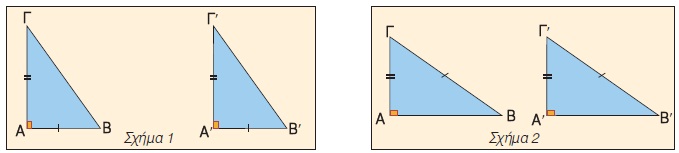
Όταν αναφερόμαστε στην ισότητα των σχημάτων, ταυτοχρόνως αναφερόμαστε και στην έννοια της συμμετρίας. Σύμφωνα με τον Vergaud, η συμμετρία είναι οπτική και λειτουργική, έχει ως αφετηρία τις πρακτικές εμπειρίες, αλλά δεν εξαρτάται μόνο από αυτές η προέλευση και η ανάπτυξή της. Γενικότερα, με τον όρο συμμετρία εννοούμε τις ισορροπημένες αναλογίες ενός σχήματος, την ακριβή αντισοιχία, που υπάρχει στο μέγεθος και στο σχήμα και τέλος, την ιδιότητα, που έχει το σχήμα, να παραμένει απαράλλαχτο.
Συμμετρία:

Στη συνέχεια, όταν αναφερόμαστε στην ομοιότητα των σχημάτων, εννοούμε τις ιδιότητες, που έχουν τα σχήματα και οι οποίες μας δείχνουν κατά πόσο δυο σχήματα μοιάζουν μεταξύ τους, έχουν, δηλαδή, το ίδιο σχήμα και το ίδιο μέγεθος.
Ομοιότητα σχημάτων:
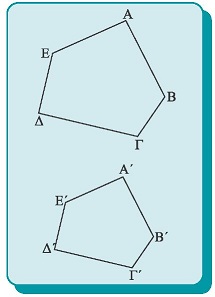
Τα παιδιά χρησιμοποιώντας αντικείμενα καθημερινής χρήσης μπορούν να φτιάξουν τις τάξεις ομοίων πραγμάτων. Μπορούν, δηλαδή, να ταξινομήσουν τα αντικείμενα- σχήματα με τέτοιο τρόπο, ώστε τα αντικείμενα- σχήματα, που είναι όμοια μεταξύ τους, να βρίσκονται στην ίδια κατηγορία.Τέλος, όταν θέλουμε να κάνουμε πιο κατανοητές τις έννοιες της ισότητας και της ομοιότητας των σχημάτων μπορούμε να χρησιμοποιήσουμε τον ορισμό της σύγκρισης. Τα παιδιά μπορούν μέσα από την σύγκριση, μεταξύ των σχημάτων, να διαπιστώσουν τις ομοιότητες και τις διαφορές, που μπορεί να υπάρχουν μεταξύ τους. Για παράδειγμα, μπορούν να συγκρίνουν τα σχήματα ανάλογα με το μέγεθός τους, πόσο μεγάλα, πόσο μικρά είναι. Επίσης, μπορούν να τα συγκρίνουν και ως προς τις πλευρές τους, ποια έχουν μεγαλύτερες πλευρές, ποια μικρότερες, ποια περισσότερες και ποια λιγότερες. Η σύγκριση, επομένως, δίνει την δυνατότητα να καταλάβουμε την ισότητα και την ομοιότητα των σχημάτων καθώς και τις διαφορές, που υπάρχουν μεταξύ τους.
Για τα παιδιά έιναι σημαντική η χρήση παιδαγωγικών υλικών, αλλά και δράσεων, για να μπορέσουν να κατανοήσουν τις έννοιες των διάφορων εννοιών, που μπορούν να τους παρουσιάζονται.
Συγκεκριμένα, για την κατανόηση της ισότητας και ομοιότητας των σχημάτων θα μπορούσαν να χρησιμοποιηθούν στην τάξη, σύμφωνα με τον van Hiele, αντικείμενα όπως: ο χάρακας, ο διαβήτης, αποκόμματα εφημερίδων, για την κατασκευή των σχημάτων, ψηφιδωτά, αλλά και διπλωμένα χαρτιά.


Επίσης, μπορούμε να δώσουμε στα παιδιά ομοιώματα αντικειμένων, που έχουν παρατηρήσει στην καθημερινή τους ζωή. Για παράδειγμα, μπορούμε να τους δώσουμε ομοιώματα από μήλα, πορτοκάλια, ντομάτες, αγγουράκια και να τους ζητήσουμε να βάλουν μαζί όλα τα όμοια αντικείμενα, να τα ταξινομήσουν κι έτσι να φτιάξουν τις τάξεις ομοίων πραγμάτων.

Επιπλέον, για να γίνουν κατανοητές κάποιες έννοιες στα μαθηματικά μπορούμε να τους τις δείξουμε μέσα από διάφορες μαθηματικές δραστηριότητες. Οι δραστηριότητες αυτές μπορούν να βοηθήσουν τα παιδιά να αναπτύξουν την νοητική τους ενεργοποίηση, για να μπορέσουν να κατανοήσουν μια κατάσταση, ένα πρόβλημα, ένα παιχνίδι. Επίσης, οι δραστηριότητες αυτές μπορούν να είναι είτε ομαδικές έιτε ατομικές και να βοηθήσουν τα παιδιά να εξοικειωθούν με τις έννοιες των μαθηματικών, που ενδέχεται να συναντήσουν τα παιδιά. Αλλά και οι δραστηριότητες συμμετρίας μπορούν να βοηθήσουν τα παιδιά να κατανοήσουν τα γενικά χαρακτηριστικά που περιγράφουν μια συμμετρική κατάσταση.
Υπάρχουν αρκετά παραδείγματα δραστηριοτήτων, όπως των Henry και Jirotkova. Σύμφωνα με αυτό το παράδειγμα ένας δάσκαλος της πρώτης τάξης δημοτικού δίνει στα παιδιά έναν κύβο και τον ονομάζει κύριο Κύβο. Ζητά, λοιπόν, από τα παιδιά να φτιάξουν ένα κοστούμι. Για να τους βοηθήσει τους δίνει το πρότυπο ενός κύβου και τετράγωνα κομματάκια χαρτί. Τα παιδιά, λοιπόν, ενώνουν πάνω στον κύβο το ένα τετράγωνο χαρτί μαζί με το άλλο. Όταν τα ενώσουν όλα τα βγάζουν και αυτό, που παρατηρούν είναι ένα ανάπτυγμα του κύβου.
Μια άλλη δραστηριότητα είναι αυτή της διατύπωσης, όπου στόχος είναι η ακριβής διατύπωση ενός αντικειμένου. Ένα παράδειγμα της συγκεκριμένης δραστηριότητας είναι οι δραστηριότητες της επικοινωνίας. Σύμφωνα με αυτή την δραστηριότητα τα παιδιά χωρίζονται σε ομάδες των δυο ατόμων και κάθονται με τις πλάτες τους γυρισμένες, ώστε να μην μπορεί να δει το ένα τι έχει το άλλο. Στη συνέχεια, το ένα από τα δυο παιδιά αρχίζει να περιγράφει το αντικείμενο και το άλλο προσπαθεί να το ανακατασκευάσει ακολουθώντας τις οδηγίες του άλλου παιδιού. Στο τέλος, τα παιδιά θα έχουν την δυνατότητα να συγκρίνουν αυτό, που έφτιαξαν με το πραγματικό αντικείμενο και μπορούν να διορθώσουν ή να επαληθεύσουν την ορθότητα της επικοινωνίας.Όσον αφορά την έννοια της ισότητας των σχημάτων χαρακτηριστικό είναι το παράδειγμα, που χρησιμοποίησε ο van Hiele. Αυτό, που πρότεινε ήταν να προσπαθήσουν τα παιδιά να τοποθετήσουν τα ίδια σχήματα το ένα δίπλα στο άλλο με τέτοιο τρόπο, ώστε να καλύψουν μια επιφάνεια, ένα δάπεδο.

Πηγή: http://images.rbs.org/cognitive/facilitating.shtml
Η δραστηριότητά μας θα έχει τον τίτλο " Κατανόηση της ισότητας και ομοιότητας σχημάτων". Στην δραστηριότητα αυτή θα συμμετέζουν 10 παιδιά ηλικίας 5-6 ετών. Τα υλικά, που θα χρησιμοποιήσουμε είναι: χαρτόνια, ψαλίδι, χαρτί, κόλλα, μολύβι. Η δραστηριότητα αυτή θα διαρκέσει 45 λεπτά, θα είναι ομαδική και θα έχει χαρακτήρα δομημένου παιχνιδιού. Οι μέθοδοι, που θα χρησιμοποιήσουμε είναι: ερωτήσεις- απαντήσεις και παρατήρηση. Οι ενότητες, που χρησιμοποιούμε είναι: Παιδί και Μαθηματικά, Παιδί και Πληροφορική και Παιδί και Γλώσσα( γραφή). Στόχος μας είναι να κάνουμε στα παιδιά κατανοητές τις έννοιες της ισότητας και της ομοιότητας μέσα από αντικείμενα, που βλέπουν στην καθημερινότητά τους.
Αφόρμηση: Το πρωί στην γωνιά της παρεούλας συζητάμε με τα παιδιά τι έκαναν την προηγούμενη μέρα. Μόλις μας που όλα τα παιδιά τι έκαναν τους λέμε ότι την προηγούμενη μέρα πήγαμε στον μανάβη της γειτονιάς μας και αγοράσαμε τα φρούτα, που βγαίνουν αυτή την εποχή, το καλοκαίρι. Μόλις πούμε στα παιδιά αυτό το γεγονός θα αρχίσουμε να τους κάνουμε κάποιες ερωτήσεις, που θα μας βοηθήσουν στην συνέχεια να τα εισάγουμε στο θέμα, που έχουμε για δραστηριότητα.
Ενδεικτικές ερωτήσεις: Τι εποχή έχουμε; Ποια φρούτα του καλοκαιριού ξέρετε; Τι σχήμα έχουν τα φρούτα, που είπατε; Τι χρώμα έχουν; Με τι μοιάζουν ( είναι, δηλαδή, κύκλος, τρίγωνο, κύλινδρος); Μοιάζουν τα φρούτα, που είπατε μεταξύ τους
Μόλις ολοκληρωθούν οι ερωτήσεις και οι απαντήσεις θα δείξουμε στα παιδιά ένα μήλο και θα τα ρωτήσουμε τι είναι αυτό, που τους δείχνουμε ( φρούτο ή λαχανικό), αν ξέρουν πως το λένε, τι χρώμα έχει και ποιο είναι το σχήμα του. Στη συνέχεια, θα τους δείξουμε ένα πορτοκάλι και θα τους κάνουμε τις ίδιες ερωτήσεις. Μόλις ολοκληρωθεί αυτή η διαδικασία θα τους δείξουμε και τα δυο φρούτα και θα τους ζητήσουμε να τα παρατηρήσουν και να μας πουν τι είναι αυτό που παρατηρούν ( αν είναι όμοια κι αν είναι ίσα). Μόλις μας πουν τις απόψεις τους θα τους εξηγήσουμε, με το παράδειγμα του μήλου και του πορτοκαλιού, τι εννοούμε με τον όρο όμοια και ίσα.
Στη συνέχεια, θα πάμε με τα παιδιά στην γωνιά του υπολογιστή και θα ψάξουμε να βρούμε τα φρούτα, που μας είπαν καθώς κι άλλα φρούτα, που μπορεί να μην ήξεραν ότι τα τρώμε το καλοκαίρι. Με αυτό τον τρόπο θα έχουμε την δυνατότητα να δουν τα παιδιά καλύτερα το σχήμα, που έχουν τα φρούτα. Μπορούν κατά τη διάρκεια αυτής της διαδικασίας να ζωγραφίζουν σε ένα χαρτί, όπως μπορούν, τα φρούτα, που δεν ξέρουν. Μετά θα ζητήσουμε από κάθε παιδί να ζωφραφίσει στον υπολογιστή, με την δική μας βοήθεια και καθοδήγηση, από ένα φρούτο , στη συνέχεια θα τα εκτυπώσουμε και κάθε παιδί θα γράψει, όπως μπορεί, το όνομα, που έχει το κάθε φρούτο. Προηγουμένως, θα έχουμε δείξει στα παιδιά την διαδικασία, που χρειάζεται, για να ζωγραφίσουμε στον υπολογιστή. Στη συνέχεια, θα κολλήσουμε τα χαρτιά με τα φρούτα, στα οποία τα παιδιά θα έχουν γράψει, με τον δικό τους τρόπο, το όνομα, που έχει το κάθε φρούτο, στα τετράγωνα χαρτόνια, που θα έχουμε κόψει μαζί με τα παιδιά. Μόλις ολοκληρώσουμε αυτή την διαδικασία θα χωρίσουμε τα παιδιά σε ομάδες 2-3 ατόμων και θα τους ζητήσουμε να κατατάξουν τα φρούτα με όποιο τρόπο θέλουν και στην συνέχεια να παρουσιάσουν αυτό, που έφτιαξαν και στα υπόλοιπα παιδιά.
Για να μπορέσουμε να δουμε αν τα παιδιά μπόρεσαν να κατανοήσουν τις έννοιες της ισότητας και της ομοιότητας των σχημάτων θα τους ζητήσουμε να εξηγούν στα υπόλοιπα παιδιά τους λόγους που κατέταξαν τα φρούτα με τον τρόπο, που επέλεξαν και θα τα παροτρύνουμε να κάνουν με τα υπόλοιπα παιδιά διάλογο, ρωτώντας κάθε φορά τα παιδιά, που παρατηρούν, γιατί τα κατέταξαν με αυτό τον τρόπο και από την μεριά τους τα παιδιά, που παρουσιάζουν μπορούν να ρωτούν τα υπόλοιπα παιδιά να τους πουν για ποιον λόγο πιστεύουν ότι τα κατέταξαν έτσι, αλλά και να τους προτείνουν εναλλακτικές μεθόδους κατάταξης.
Κολέζα, Ε. (2009). Θεωρία και Πράξη στη Διδασκαλία των Μαθηματικών. Εκδόσεις Τόπος Αθήνα.Κολέζα, Ε. (2009). Θεωρία και Πράξη στη Διδασκαλία των Μαθηματικών. Εκδόσεις Τόπος Αθήνα.
Τζεκάκη, Μ. (2007) Μικρά παιδιά, μεγάλα μαθηματικά νοήματα : Προσχολική και πρώτη σχολική ηλικία. Παιδαγωγική Σειρά. Αθήνα : Gutenberg - Γιώργος & Κώστας Δαρδανός
Σαλβάρας, Γ. Η διδακτική μαθηματικών δημοτικού σχολείου. Παλλήνη-Αττικής: Εκδόσεις Εκπαιδευτήρια Κωστέα- Γείτονα.