Οι περιπέτειες του Πυθαγόρα και της Πυθαϊδας στην χώρα των τετραπλεύρων
Submitted by vernikou on Sat, 06/15/2013 - 17:06Το θέμα το οποίο θα διδάξουμε με αυτή την διδασκαλία είναι η ανάπτυξη λεξιλογίου για τις ιδιότητες των γεωμετρικών σχημάτων (π.χ. τετράπλευρα). Συγκεκριμένα, το θέμα ανήκει στο κεφάλαιο της Γεωμετρίας. Αρχικά το διδάσκουμε αυτό για να έχουν μια γενική εικόνα των σχημάτων μέσα από την οποία θα αποκτήσουν την ικανότητα να ξεχωρίζουν τη συγκεκριμένη κατηγορία σχημάτων, δηλαδή τα τετράπλευρα, με βάση τα χαρακτηριστικά τους (π.χ. τέσσερις πλευρές). Θεωρούμε αυτό το θέμα σημαντικό διότι βοηθά στην περαιτέρω ανάπτυξη της γεωμετρικής σκέψης των παιδιών.
Η μαθηματική έννοια στην οποία θα αναφερθούμε η ανάπτυξη λεξιλογίου για τις ιδιότητες γεωμετρικών σχημάτων και συγκεκριμένα για τα τετράπλευρα. Στο βιβλίο της Ευγενίας Κολέζα, (2οοο), αναφέρεται ο ορισμός του Fischbein για τα γεωμετρικά σχήματα. Συγκεκριμένα ως γεωμετρικά σχήματα ορίζονται οι νοητικές οντότητες (mental entities), όπου ο χαρακτήρας τους είναι και εννοιολογικός (conceptual) ,αλλά και σχηματικός (figural). Γι'αυτό το λόγο κιόλας τα γεωμετρικά σχήματα τα ονομάζει σχηματικές έννοιες (Figural concepts). Ουσιαστικά τα γεωμετρικά σχήματα ως έννοια αποτελούνται από τον ορισμό (the definition), την εικόνα (the images) και τη σχηματική έννοια (the figural concept). Ο ίδιος το εξηγεί αυτό με τον εξής τρόπο: “Ένα σχέδιο (drawing/the image) δεν είναι αυτό το ίδιο το γεωμετρικό σχήμα, αλλά μια γραφική συγκεκριμένη υλική παρουσίασή του. Το γεωμετρικό σχήμα είναι η ιδέα που αντιστοιχεί στο σχέδιο, η αφηρημένη ιδεατή, εξαϋλωμένη οντότητα(the figural concept) που καθορίζεται επακριβώς από τον ορισμό (the definition).
Ένας άλλος απλός ορισμός που υπάρχει για τα γεωμετρικά σχήματα είναι ένα εύκολο σημείων στο χώρο και σύμφωνα με την ευκλείδεια γεωμετρία (Αργυρόπουλος , Βλάμος, Κατσούλης, Μαρκάτης, Σιδέρης, 2000), τα αρχικά σχήματα είναι το σημείο, η ευθεία και το επίπεδο.
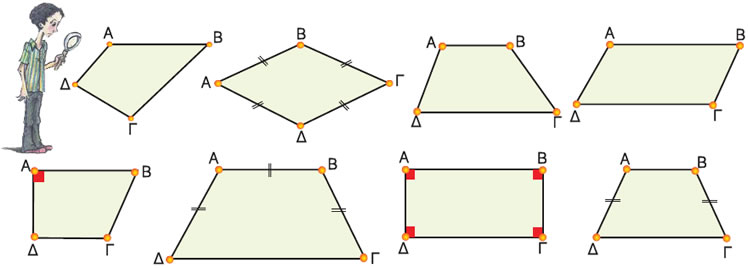
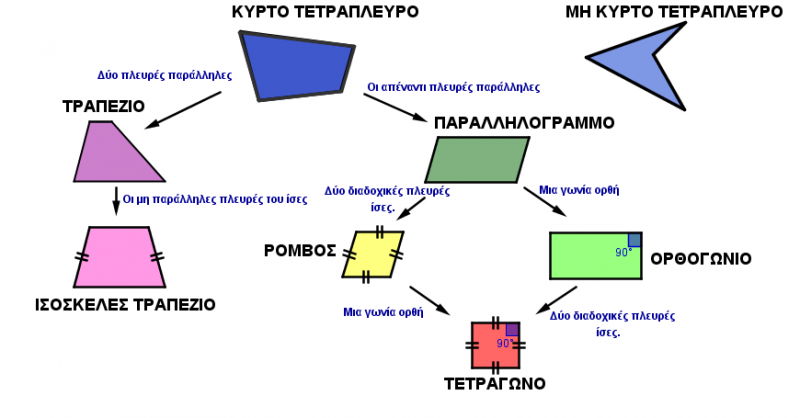
Ως προς τα τετράπλευρα, μπορούσε να πούμε ότι είναι τα γεωμετρικά σχήματα, τα οποία έχουν τέσσερις πλευρές. Πιο γνωστά σε μας είναι τα κυρτά τετράπλευρα ,στα οποία εντάσσονται δύο κατηγορίες: Τα παραλληλόγραμμα και τα τραπέζια.
Στην ευκλείδεια γεωμετρία ,στα παραλληλόγραμμα ανήκουν το ορθογώνιο παραλληλόγραμμο που έχει τέσσερις γωνίες ορθές ,ο ρόμβος που έχει τέσσερις πλευρές ίσες και το τετράγωνο που έχει τέσσερις γωνίες ορθές και τέσσερις πλευρές ίσες. Από την άλλη, υπάρχει το τραπέζιο που έχει μόνο δύο πλευρές παράλληλες και το ισοσκελές τραπέζιο που οι μη παράλληλες πλευρές του είναι ίσες.
Στόχοι-Γιατί διδάσκουμε αυτή την μαθηματική έννοια
Αρχικά, σύμφωνα με το νέο Αναλυτικό Πρόγραμμα, προτείνεται τα παιδιά να μπορούν, μέσω της διδασκαλίας αυτής της μαθηματικής έννοιας να:
1)Αναγνωρίζουν, να ονομάζουν και να ταξινομούν τα βασικά επίπεδα γεωμετρικά σχήματα με βάση τα χαρακτηριστικά τους και σε ποικιλία θέσεων ,μεγεθών και προσανατολισμών
2)Να περιγράφουν επίπεδα γεωμετρικά σχήματα, χρησιμοποιώντας τα στοιχεία και τις ιδιότητες
3)Να κατασκευάζουν επίπεδα γεωμετρικά σχήματα με διάφορα μέσα
4)Να συνθέτουν και να αναλύουν απλά επίπεδα γεωμετρικά σχήματα σε δύο ή περισσότερα μέρη
Επιπρόσθετα κάποιοι άλλοι στόχοι που τίθενται από τη Τζεκάκη είναι οι παρακάτω:
1)Να αντιλαμβάνονται τα αντικείμενα και τις μεταξύ τους σχέσεις μέσω της κιναισθησίας.
2)Να χτίζουν συστηματικές γνώσεις για τις χωρικές ιδιότητες και σχέσεις των αντικειμένων.
3)Να αντιστοιχίζουν χώρους, οι οποίοι βρίσκονται σε διαφορετικά μεγέθη.
4)Να αναπτύσσουν δεξιότητες για να δημιουργούν και να χρησιμοποιούν διάφορες χωρικές αναπαραστάσεις.
5)Να αναγνωρίσουν και να καταλάβουν ότι σχετίζεται με τα μαθηματικά και το οποίο υπάρχει στο γεωμετρικό περιβάλλον(Τζεκάκη)
Ως προς το “γεωμετρικό συλλογισμό”, που έχει να κάνει με το πώς οργανώνουμε και επεξεργαζόμαστε έναν βιωμένο χώρο με βάση γεωμετρικά μοντέλα, τα παιδιά θα μπορούν να:
1)Αναγνωρίζουν, να περιγράφουν και να αναλύουν τις κατηγορίες, τις ιδιότητες και τις ιδιότητες των κατηγοριών των γεωμετρικών σχημάτων.
2)Να αναλύουν και να συνθέτουν ή να ανασυνθέτουν σε άλλα σχήματα.
Διδάσκοντας τη συγκεκριμένη μαθηματική έννοια, δηλαδή την ανάπτυξη λεξιλογίου για τις ιδιότητες των τετραπλεύρων, τα παιδιά θα μπορέσουν να κατανοήσουν καλύτερα τον κόσμο γύρω τους, αλλά και να τον εξηγήσουν. Πιο συγκεκριμένα, θα μπορέσουν να συνειδητοποιήσουν το γεγονός ότι τα γεωμετρικά σχήματα μπορούμε να συναντήσουμε παντού στην καθημερινή μας ζωή και ακόμα μπορούμε να τα χρησιμοποιήσουμε συνειδητά ή ασυνείδητα για ποικίλους λόγους, είτε ατομικούς, είτε συλλογικούς.
Ο χώρος και γενικά ότι βιώνουμε μέσα σε αυτόν, βοηθούν στη ανάπτυξη της μαθηματικής σκέψης των παιδιών και αποτελεί το θεμέλιο της.(Τζεκάκη, 2007). Σύμφωνα με έρευνες που έχουν γίνει, η κατανόηση του χώρου βοηθάει αρκετά τα παιδιά στο να τα πηγαίνουν καλύτερα στα μαθηματικά. Έτσι, κατακτώντας την ικανότητα να προσανατολίζονται στο χώρο, θα γνωρίζουν και το πού βρίσκονται αλλά και το πώς θα μπορέσουν να κινηθούν στο κόσμο.( Καφούση, Σκουμπουρδή, 2008).
Επιπλέον, ως προς τη γεωμετρική σκέψη, ο Freudenthal, αναφέρει ότι δεν αρκεί μόνο η παρατήρηση γεωμετρικών αντικειμένων για την ανάπτυξη αυτού του είδους σκέψης, αλλά είναι απαραίτητο τα παιδιά να αρχίζουν να διαχειρίζονται και να μελετάνε αντικείμενα, όμως υπό την προϋπόθεση ότι θα μετατρέψουνε τα πραγματικά αντικείμενα σε μη πραγματικά(δηλαδή νοερά) και να τους δώσουν τη μορφή σχήματος.( Τζεκάκη, 2007)
Τα επίπεδα γεωμετρικής σκέψης κατά τον Van Hiele
Επίπεδο 1: (αναγνώριση/recognition) Τα παιδιά αντιλαμβάνονται τα γεωμετρικά σχήματα ως καθολικά (Gestalt) και όχι σε σχέση µε τα χαρακτηριστικά τους. Για την περιγραφή των σχημάτων χρησιμοποιούν οπτικά μέσα (π.χ. αναγνωρίζουν ένα ορθογώνιο επειδή μοιάζει µε πόρτα).
Επίπεδο 2: (ανάλυση/analysis) Τα παιδιά αναγνωρίζουν τα σχήματα µε τη βοήθεια των χαρακτηριστικών τους, µπορούν να τα ανακαλύπτουν και να τα περιγράφουν, αλλά δεν µπορούν να τα ορίσουν. Αν τα ρωτήσουμε γιατί αυτό το σχήµα είναι ορθογώνιο, τότε θα µας πουν κάποια από τα χαρακτηριστικά του ορθογωνίου (όπως: τα τετράπλευρα έχουν τέσσερις πλευρές κ.τ.λ.).
Επίπεδο 3: (διάταξη/order) Τα παιδιά μπορούν να κατηγοριοποιήσουν τα σχήματα και τα χαρακτηριστικά τους και αρχίζουν να κατανοούν το ρόλο του ορισµού, αλλά δεν μπορούν να δουλέψουν στα πλαίσια του μαθηματικού συστήματος.
Επίπεδο 4: (παραγωγικός συλλογισµός/deduction) Τα παιδιά καταλαβαίνουν τη σηµασία του παραγωγικού συλλογισµού και τους ρόλους των αξιωµάτων, των θεωρηµάτων και της απόδειξης.
Επίπεδο 5: (αυστηρότητα/rigor) Τα παιδιά μπορούν να κατανοήσουν και είναι σε θέση να κάνουν αφηρηµένους παραγωγικούς συλλογισµούς.(Κολέζα, 2000, Van De Walle, 2007)
Ένα παράδειγμα το οποίο είναι εφαρμοσμένο πάνω στα επίπεδα που έχει προτείνει ο Van Hiele , είναι το εξής:
για τη μελέτη του ρόμβου προτείνει τα εξής στάδια κατά τη διδασκαλία:
Πρώτο στάδιο: Επιδεικνύεται ένα συγκεκριμένο σχήμα που αποκαλείται «ρόμβος». Παρουσιάζονται στους μαθητές κι άλλα γεωμετρικά σχήματα και το ερώτημα που τίθεται είναι αν και αυτά είναι επίσης ρόμβοι.
Δεύτερο στάδιο: Ο ρόμβος διπλώνεται ως προς τους άξονες συμμετρίας του. Γίνονται κάποιες παρατηρήσεις σχετικά με τις διαγώνιες και τις γωνίες του ρόμβου.
Τρίτο στάδιο: Οι μαθητές ανταλλάσουν ιδέες ως προς τις ιδιότητες του ρόμβου.
Τέταρτο στάδιο: Δίνονται κάποια στοιχεία του ρόμβου π.χ. πλευρά και γωνία και ζητείται να κατασκευαστεί το σχήμα.
Πέμπτο στάδιο: Οι ιδιότητες του ρόμβου ανακεφαλαιώνονται και απομνημονεύονται. Ο ρόμβος εντάσσεται λειτουργικά στην οικογένεια των τετράπλευρων.»
Όσο αφορά τις γνώσεις των μαθητών, με βάση τα επίπεδα αυτά, έχει αποδειχθεί ότι πολλά παιδιά, διαφόρων ηλικιών, βρίσκονται σε ένα από τα αρχικά στάδια ανάπτυξης της γεωμετρικής σκέψης. Αυτό εξαρτάται από το πόσο ασχολείται το άτομο με συγκεκριμένα γεωμετρικά αντικείμενα.(Τζεκάκη, 2010).
Σε σχέση με τη θεωρία του Van Hiele, ο Piaget και οι συνεργάτες του, πιστεύουν ότι το παιδί χρειάζεται ένα χρονικό διάστημα εξάσκησης, δύο χρόνων, για να καταφέρει να ξεχωρίζει το τετράγωνο από το ρόμβο όχι μόνο εμφανισιακά (π.χ. αποτυπώνοντάς τα στο χαρτί), αλλά και για άλλους λόγους, όπως σύμφωνα με τις ιδιότητές τους.
Από την άλλη, οι Dickosn et all. , έχουν κάνει κάποια προσαρμογή στα επίπεδα του Van Hiele, η οποία είναι η εξής:
Επίπεδο 1: Αναγνώριση των σχημάτων από τα παιδιά, όχι με βάση τα χαρακτηριστικά και τις ιδιότητες.
Επίπεδο 2: Τα παιδιά αποκτούν την ικανότητα του να αντιλαμβάνονται και να περιγράφουν μέρη και ιδιότητες σχημάτων.
Επίπεδο 3: Ικανότητα εξήγησης και ορισμού των σχημάτων και η κατηγοριοποίηση τους με βάση τις ιδιότητες.
Επίπεδο 4: Βγάζουν συμπεράσματα για τις ιδιότητες και τις σχέσεις των σχημάτων.
Επίπεδο 5: Φτάνουν στο σημείο να κατανοήσουν την έννοια της Γεωμετρία.
Συμπερασματικά, η θεωρία επιπέδων του Van Hiele έχει κάποια αδύναμα σημεία. Ειδικότερα. Δεν μπορεί κάποιος εύκολα να καταλάβει με ακρίβεια ποιο είναι επίπεδο σκέψης των παιδιών.(Κολέζα, 2000).
Κάποιες έρευνες, σχετικά με τα επίπεδα του Van Hiele και την εκμάθηση των γεωμετρικών σχημάτων, αναφέρουν ότι τα παιδιά αναγνωρίζουν κάποια σχήματα, αλλά τα ταυτίζουν με ένα πρότυπο. Για παράδειγμα, άμα τα ρωτήσεις «Γιατί αυτό είναι ορθογώνιο;» μπορεί να σου απαντήσει «Γιατί είναι σαν την πόρτα». Ακόμα, σύμφωνα με άλλες έρευνες, το επίπεδο δύο χωρίζεται σε 3 κατηγορίες: η 1η κατηγορία αφορά παιδιά που μπορούν να εντοπίσουν πολλά χαρακτηριστικά στο σχήμα, δεν μπορούν όμως όμως να τα περιγράψουν. Στη 2η κατηγορία ανήκουν τα παιδιά που μπορούν να βρουν και να περιγράψουν μόνο ένα χαρακτηριστικό. Και στη 3η και τελευταία κατηγορία, τα παιδιά μπορούν να βρουν και να περιγράψουν τα χαρακτηριστικά των σχημάτων.(Τζεκάκη, 2010).
Μια άλλη έρευνα, σχετίζεται με την αναγνώριση σχημάτων από τα παιδιά, ηλικίας 4-6 ετών. Αυτή η έρευνα έδειξε ότι από τα τετράπλευρα το πιο αναγνωρίσιμο σχήμα είναι το τετράγωνο, το οποίο μπορούν και το αναγνωρίζουν, χωρίς να ξέρουν το λόγο. Αμέσως μετά πιο αναγνωρίσιμο σχήμα είναι το ορθογώνιο. Ως προς την αναγνώριση των σχημάτων, μελετητές έχουν βρει παράγοντες, οι οποίοι την επηρεάζουν. Αυτοί οι παράγοντες, είναι η οικειότητα με το σχήμα, ο προσανατολισμός του σχήματος και η ιδιαίτερη μορφή του. Γενικά, μπορούμε να πούμε ότι είναι δύσκολο για ένα παιδί να καταλάβει κάποια αντικείμενα, ως μια γεωμετρική έννοια. Τα συνδέουν περισσότερα με εμπειρίες και βιώματα τους. Επιπλέον, όσο αφορά τη διάκριση των σχημάτων, συγκεκριμένα τα τετράπλευρα, μπορεί να ειπωθεί ότι τα παιδιά μπερδεύουν αρκετά κάποια σχήματα, όπως το τετράγωνο με το ρόμβο. Δεν ισχύει όμως αυτό για όλα. Χαρακτηριστικό παράδειγμα, το τετράγωνο με το ορθογώνιο.
Ας αναφερθούμε και σε μια άλλη έρευνα, των Iliada, Gagatsis & Kyriakides, η οποία είναι η εξής: «Για τη μελέτη του τρόπου με τον οποίο τα παιδιά 5-7 χρόνων αντιλαμβάνονται αυτές τις αλλαγές, τους ζητήθηκε να κάνουν μια «σκάλα» με τρίγωνα, τετράγωνα και ορθογώνια, ώστε το κάθε επόμενο ναι είναι μεγαλύτερο από το προηγούμενο. Τα παιδιά κατασκεύασαν σχήματα είτε αυξάνοντας τη μια ή και τις δύο διαστάσεις δείχνοντας να κατανοούν αυτή τη διαφορά στις ιδιότητες. Σε άλλες δράσεις όπου τους ζητήθηκε να δημιουργήσουν ένα συνεχές από ένα πολύ λεπτό ορθογώνιο ως ένα τετράγωνο κατέληξαν να αποκαλέσουν το σχήμα που αναγνώριζαν ως τετράγωνο, αλλά προέκυψε από τον μετασχηματισμό του ορθογωνίου ως «τετράγωνο ορθογώνιο.(Iliada, Gagatsis & Kyriakides, 2004; Elia & Gagatsis, 2003).
Κλείνοντας, οι δραστηριότητες που ακολουθούν θα σχετίζονται περισσότερο με τη προσχολική και τη 1η σχολική ηλικία, συγκεκριμένα με τα επίπεδα 0, 1 και 2 του Van Hiele.
Τίτλος: Οι περιπέτειες του Πυθαγόρα και της Πυθαϊς στην χώρα των τετραπλεύρων
Ηλικία: 4-8 ετών
Προαπαιτούμενη γνώση: Κατά τη διάρκεια του συγκεκριμένου σεναρίου διδασκαλίας, τα παιδιά θα πρέπει να έχουν κάποια γνώση για τα γεωμετρικά σχήματα.
Αριθμός παιδιών: 10-15 παιδιά
Χρόνος διδασκαλίας: Η διάρκεια των δραστηριοτήτων θα είναι τρεις εβδομάδες. Κάθε βδομάδα θα πραγματοποιούνται 2 δραστηριότητες. Η πρώτη, η δεύτερη, η τρίτη και η πέμπτη θα διαρκούν περίπου ένα τέταρτο. Η τέταρτη και η δραστηριότητα αξιολόγησης διαρκούν περίπου 45 λεπτά.
Ανάπτυξη λεξιλογίου για τα τις ιδιότητες γεωμετρικών σχημάτων (π.χ. Τετράπλευρα)
Συμβατότητα με το Νέο Αναλυτικό πρόγραμμα: Το συγκεκριμένο κεφάλαιο ανήκει στην ενότητα του Νέου Αναλυτικού προγράμματος “Γεωμετρία και Μέτρηση”. Ο γενικός στόχος είναι “τα παιδιά να αναγνωρίζουν, να ονομάζουν και να ταξινομούν τα βασικά επίπεδα των γεωμετρικών σχημάτων”. Υπηρετεί τις θεμελιώδεις έννοιες διαθεματικής προσέγγισης: επικοινωνία(π.χ. Μέσω των ερωταπαντήσεων μεταξύ νηπιαγωγού και νηπίων), ανάγνωση ( π.χ. Συνταγή, βλ. Δραστηριότητα αξιολόγησης), εικαστικά (π.χ. Δημιουργία αγαπημένου ζώου μέσω τετραπλεύρων tangrams)
Γενικός σκοπός: Τα παιδιά να είναι σε θέση να αναγνωρίσουν, να ονομάσουν, και να ταξινομήσουν τα βασικά επίπεδα γεωμετρικά σχήματα.
Επιμέρους στόχοι: Τα παιδιά:
-
να περιγράφουν επίπεδα γεωμετρικά σχήματα, χρησιμοποιώντας τα στοιχεία και τις ιδιότητες
-
να κατασκευάζουν επίπεδα γεωμετρικά σχήματα με διάφορα μέσα
-
να συνθέτουν και να αναλύουν απλά επίπεδα γεωμετρικά σχήματα σε δύο ή περισσότερα μέρη
-
να αναγνωρίζουν, να περιγράφουν και να αναλύουν τις κατηγορίες, τις ιδιότητες και τις ιδιότητες των κατηγοριών των γεωμετρικών σχημάτων
Μέθοδοι διδασκαλίας: Ομαδοσυνεργατική, Διερευνητική
Τεχνικές: Εισήγηση, Παιχνίδι, Ομαδική εργασία, Ερωτήσεις-Απαντήσεις, Αξιοποίηση φύλλων εργασίας
Υλικά και μέσα: Φύλλα εργασίας, Μαρκαδόροι, Μολύβια, Επιτραπέζιο, Πιόνια, Ζάρι, Tangrams, Χαρτόνι, Φουρνάκι, Πλαστικά μαχαίρι, Μπολάκια, Βούτυρο, Ζάχαρη, Αυγό, Κανέλα, Αλάτι, Σόδα, Βανίλια, Κουτάλι, Πλάστη, Σύρμα για ανακάτεμα ζύμης, Ταψί, Λαδόκολλα, Φύλλο Α4 (ζωγραφιά)
Περιγραφή δραστηριοτήτων
1η Δραστηριότητα
Βήμα 1: Μοιράζουμε στα παιδιά τα φύλλα εργασίας και τους δίνουμε οδηγίες για το τι ακριβώς χρειάζεται να κάνουν.
Βήμα 2: Τα παιδιά αντιστοιχούν το κάθε σχήμα με τον αντίστοιχο αριθμό των πλευρών που έχει, χρησιμοποιώντας μαρκαδόρο.
Βήμα 3: Τους ρωτάμε άμα γνωρίζουν πώς ονομάζονται κάποια από τα σχήματα που βλέπουν στο φύλλο εργασίας




2η Δραστηριότητα
Βήμα 1: Αρχικά ρωτάμε τα παιδιά ποια σχήματα μπορούν να εντοπίσουνε σε διάφορα αντικείμενα του σπιτιού τους (π.χ. Τηλεόραση που μοιάζει με ορθογώνιο).
Βήμα 2: Στη συνέχεια, τους μοιράζουμε το φύλλο εργασίας και τους ζητάμε να εντοπίσουν ποια σχήματα βλέπουν στην εικόνα και να κυκλώσουν μόνο αυτά που έχουν τέσσερις πλευρές, δηλαδή τα τετράπλευρα.
3η Δραστηριότητα
Ο Πυθαγόρας έκανε μια ζωγραφιά στο σχολείο του. Όμως ο σκύλος του, ο Μπούμπη, του την έσκισε καταλάθως. Ζητάμε λοιπόν από τα παιδιά να μας πουν πώς ονομάζονται τα τετράπλευρα στα οποία κόπηκε η ζωγραφιά και να βοηθήσουν στη συνέχεια τον Πυθαγόρα να ενώσει τα κομμάτια της ζωγραφιάς του.
4η Δραστηριότητα
Ο Πυθαγόρας και η Πυθαϊς παίζανε στη σοφίτα του σπιτιού τους, όπου και βρήκαν ένα επιτραπέζιο παιχνίδι. Προτρέπουμε τα παιδιά να παίξουνε μαζί τους. Χωρίζουμε τα παιδιά σε ομάδες τριών με τεσσάρων ατόμων. Τα παιδιά καλούνται να κουνήσουν το πιόνι τους τόσα κουτάκια, όσα λέει το ζάρι. Κάθε φορά ρίχνει το ζάρι διαφορετικό μέλος της ομάδας. Στο κουτάκι που σταματάνε, τους ζητάμε να μας πουν αν είναι τετράπλευρο ή όχι το σχήμα. Σε περίπτωση που είναι τετράπλευρο, πρέπει να το αναγνωρίσουν. Αποφασίζει όλη η ομάδα μαζί για την απάντηση που θα δοθεί. Αν όμως δώσουν λάθος απάντηση πάνε πίσω δύο τετράγωνα. Κερδίζει η ομάδα που θα καταφέρει να φτάσει στο τέλος.
5η Δραστηριότητα
Ο Πυθαγόρας και η Πυθαϊς ζητάνε από τα παιδιά να φτιάξουν το αγαπημένο τους ζώο χρησιμοποιώντας tangrams (τετράπλευρα).
Δραστηριότητα αξιολόγησης
Η Πυθαϊς ζητάει από τα παιδιά να τη βοηθήσουν να φτιάξει τα αγαπημένα τετράπλευρα μπισκότα του Πυθαγόρα ως δώρο για τη γιορτή του. Τα παιδιά χωρίζονται σε τρεις ομάδες. Η πρώτη ομάδα αναλαμβάνει την ανάγνωση της συνταγής, η δεύτερη ομάδα τοποθετεί και ανακατεύει τα υλικά στα μπολ και η τρίτη ομάδα ανοίγει τη ζύμη και τη κόβει με τα πλαστικά μαχαίριαν σε τετράπλευρα σχήματα. Αφού τα ψήσουν, θα μπορούν στη συνέχεια και να τα απολαύσουν.
Το σενάριο διδασκαλίας βασίζεται κυρίως στο πρώτο και στο δεύτερο επίπεδο του Van Hiele. Συγκεκριμένα, επιλέξαμε την πρώτη δραστηριότητα για να ξεκινήσουμε από κάτι γενικό (όλα τα γεωμετρικά σχήματα) και να φτάσουμε σε κάτι πιο ειδικό (δηλαδή τα τετράπλευρα). Η δεύτερη δραστηριότητα βασίστηκε κυρίως στο πρώτο επίπεδο του Van Hiele και στο βιβλίο “Μικρά παιδιά μεγάλα μαθηματικά νοήματα – Προσχολική και πρώτη σχολική ηλικία” της Μ. Τζεκάκη, σύμφωνα με το οποίο υποστηρίζεται ότι είναι απαραίτητο τα παιδιά να αρχίζουν να διαχειρίζονται και να μελετάνε αντικείμενα υπό την προϋπόθεση ότι θα μετατρέψουν τα πραγματικά αντικείμενα σε νοερά δίνοντας τους τη μορφή κάποιου σχήματος. Η τρίτη, η τέταρτη και η πέμπτη δραστηριότητα είναι επηρεασμένες από το δεύτερο επίπεδο του Van Hiele. Μέσα από τις δραστηριότητες αυτές, τα παιδιά είναι απαραίτητο να αναγνωρίσουν, να ανακαλύψουν και να περιγράψουν γεωμετρικά σχήματα περισσότερο με βάση τα χαρακτηριστικά τους. Ειδικότερα, η δραστηριότητα με το επιτραπέζιο επιλέχθηκε τέταρτη για να γίνει πιο ευχάριστη και ψυχαγωγική η μάθηση των τετραπλεύρων και για να υπάρχει ενδιαφέρον γι'αυτά από τα παιδιά.
Ερωτήματα εκπαιδευτικού στα πλαίσια των δραστηριοτήτων(Ενδεικτικά)
1η Δραστηριότητα
Γνωρίζετε κάποια από τα σχήματα; (προφορικά)
Ο Πυθαγόρας και η Πυθαϊς θέλουν να μάθουν πόσες πλευρές έχει το κάθε σχήμα. Μπορείς να τους βοηθήσεις; (γραπτά στο φύλλο εργασίας και προφορικά)
2η Δραστηριότητα
Ποια σχήματα μπορείτε να δείτε σε διάφορα αντικείμενα ;(προφορικά)
Στο δωμάτιο της Πυθαϊς υπάρχουν πολλά αντικείμενα σε διάφορα σχήματα .Μπορείς να τα βρεις; Ποια σχήματα βλέπετε στην παραπάνω εικόνα; Κύκλωσε όσα έχουν τέσσερις πλευρές. ( γραπτά στο φύλλο εργασίας και προφορικά)
3η Δραστηριότητα
Πώς ονομάζονται τα τετράπλευρα στα οποία κόπηκε η ζωγραφιά του Πυθαγόρα; (προφορικά)
4η Δραστηριότητα
Πιστεύεις ότι αυτό το σχήμα είναι τετράπλευρο ή όχι; Πώς νομίζεις ότι λέγεται αυτό το τετράπλευρο; (προφορικά)
5η Δραστηριότητα
Το αγαπημένο ζώο του Πυθαγόρα είναι ο σκύλος, ενώ της Πυθαϊς το κουνέλι. Ποιο είναι το δικό σου αγαπημένο ζωάκι; Φτιάξ'το με την βοήθεια των tangrams. (προφορικά)
Δραστηριότητα Αξιολόγησης
Μπορείς να μου πεις δύο από τα υλικά που χρειαζόμαστε για τη συνταγή; Δηλαδή σε ποια σχήματα θα κάνουμε τα μπισκότα; ( προφορικά)
ΠΑΡΑΡΤΗΜΑ
ΥΛΙΚΑ
(Όλα τα παρακάτω,εκτός από τα πιόνια, το ζάρι και τα tangrams, είναι κατασκευασμένα από εμάς)
1η Δραστηριότητα (1ο φύλλο εργασίας)

2η Δραστηριότητα (2ο φύλλο εργασίας)

3η Δραστηριότητα (Ζωγραφιά Πυθαγόρα)
 4η Δραστηριότητα (Επιτραπέζιο)
4η Δραστηριότητα (Επιτραπέζιο)



5η Δραστηριότητα (Αγαπημένα ζωάκια με tangrams)

Χαρακτηριστικό παράδειγμα:
 Δραστηριότητα αξιολόγησης (Συνταγή)
Δραστηριότητα αξιολόγησης (Συνταγή)

Αργυρόπουλος,Η., Βλάμος,Π., Κατσούλης, Γ., Μαρκάτης,Σ.,Σιδέρης,Π. (2001). Ευκλείδεια Γεωμετρία (Α' και Β' Tάξη). Αθήνα: ΟΕΔΒ.
Καφούση, Σ., & Σκουμπουρδή, Χ. (2008). Τα μαθηματικά των παιδιών 4-6 ετών: Αριθμοί και χώρος. Αθήνα: Εκδ. Πατάκης.
Κολέζα, Ε. Γ. (2000). Γνωσιολογική και διδακτική προσέγγιση των στοιχειωδών μαθηματικών εννοιών. Επιστημολογία και Διδακτική των Μαθηματικών και Φυσικών Επιστημών. Αθήνα : Leader Books
Τζεκάκη, Μ. (2010). Μαθηματική Εκπαίδευση για την Προσχολική και Πρώτη Σχολική Ηλικία. Θεσσαλονίκη: Ζυγός.
Τζεκάκη, Μ. (2007) Μικρά παιδιά, μεγάλα μαθηματικά νοήματα : Προσχολική και πρώτη σχολική ηλικία. Παιδαγωγική Σειρά. Αθήνα : Gutenberg - Γιώργος & Κώστας Δαρδανός
Van de Walle, J. A. (2007). Μαθηματικά για το Δημοτικό και το Γυμνάσιο: Μια εξελικτική διδασκαλία. Αθήνα: Επίκεντρο.