Ο πολλαπλασιασμός ως επαναλαμβανόμενη πρόσθεση
Submitted by valiappii on Fri, 06/14/2013 - 18:51
Στη πιο απλή της ερμηνεία μία μαθηματική πράξη είναι μία διαδικασία που παράγει μία νέα τιμή .Αυτή η νέα τιμή μπορεί να προέρχεται μετά από πρόσθεση , αφαίρεση , πολλαπλασιασμό, διαίρεση. Οι πράξεις εμφανίζονται συχνά στην καθημερινότητα μας και είναι πολύ σημαντικό να τις κατανοήσουν τα παιδιά από μικρή ηλικία. Μια από τις πράξεις που είναι απαραίτητο να κατανοήσουν και να χρησιμοποιούν τα παιδιά είναι η πρόσθεση. Η πρόσθεση αποτελεί την βάση όλων των πράξεων ενώ επίσης αποτελεί μοντέλο για σχετικές πράξεις όπως ο πολλαπλασιασμός.
Ο πολλαπλασιασμός όπως αναφέραμε είναι μια διαδικασία επαναλαμβανόμενης πρόσθεσης και γι’ αυτό το λόγο η διδασκαλία του είναι ανάλογη με την πρόσθεση. Σε μια έρευνά του ο Piaget τόνισε ότι τα παιδιά για να κατανοήσουν τον πολλαπλασιασμό και την διαίρεση πρέπει να έχουν περάσει στο στάδιο της νοητικής σκέψης που απαιτείται: δηλαδή, θα πρέπει να έχουν εμπεδώσει τις έννοιες της πρόσθεσης και της αφαίρεσης, ώστε να μπορέσουν να εργαστούν με κάτι πιο πολύπλοκο, όπως είναι ο πολλαπλασιασμός. Αυτό συμβαίνει διότι στην πρόσθεση ο συλλογισμός που ακολουθείται είναι αθροιστικός, δηλαδή τα αντικείμενα ενώνονται, ενώ στον πολλαπλασιασμό τα αντικείμενα δεν ενώνονται απλώς αλλά τα παιδιά πρέπει να κατανοήσουν έννοιες όπως η αναλογία και η αντιστοίχιση ένα προς πολλά.
Ένας εύκολος τρόπος για τη διδασκαλία του πολλαπλασιασμού στα παιδιά είναι να τα βοηθήσουμε να κατανοήσουν τον πολλαπλασιασμό ως επαναλαμβανόμενη πρόσθεση. Για παράδειγμα η μαθηματική πράξη του πολλαπλασιασμού 2Χ3 μεταφράζεται στην επαναλαμβανόμενη πρόσθεση σαν 2+2+2. Για την επίτευξη του στόχου μας, δηλαδή να κατανοήσουν τα παιδιά τον πολλαπλασιασμό, δεν πρέπει να ξεχνάμε το σημαντικό ρόλο της ρεαλιστικής προσέγγισης στη διδασκαλία των μαθηματικών. Η βιωματική προσέγγιση δεν ασχολείται με αφηρημένες έννοιες και κανόνες που στοχεύουν σε συγκεκριμένες λειτουργίες. Αντιθέτως, στρέφει το ενδιαφέρον της στην οικοδόμηση της γνώσης από τα ίδια τα παιδιά. Σκοπός λοιπόν είναι να εξάψουμε το ενδιαφέρον των παιδιών και ν’ ασχοληθούν με μαθηματικά προβλήματα και αντικείμενα της καθημερινότητας τους, ώστε να μην οικειοποιηθούν απλώς τις μαθηματικές έννοιες, ως κάτι γενικό και αφηρημένο, αλλά να μπορούν να τις χρησιμοποιούν άρτια. Η συγκεκριμένη μέθοδος βασίζεται πάνω στις εξής αρχές:
1. <<Η καθοδηγούμενη επανα-ανακάλυψη>>: Σύμφωνα με την αρχή αυτή πρέπει να δημιουργήσουμε στα νήπια μαθηματικές καταστάσεις ακολουθώντας τους δρόμους της εξέλιξης που ακολούθησε η μαθηματική επιστήμη. Να δημιουργήσουμε δηλαδή στα παιδιά εμπειρίες αντίστοιχες με αυτές που οδήγησαν στην ανακάλυψη των μαθηματικών που θέλουμε να διδάξουμε.
2. <<Η διδακτική φαινομενολογία>>: Σύμφωνα με την παραπάνω αρχή τα μαθηματικά πλαίσια μέσα στα οποία επιχειρούμε να περάσουμε στα παιδιά μια συγκεκριμένη μαθηματική γνώση πρέπει να έχουν μελετηθεί προσεκτικά ως προς τα εξής σημεία: Αρχικά θα χρειαστεί να έχουμε σκεφτεί εκ των προτέρων τις στρατηγικές μάθησης που θα χρησιμοποιήσουμε και δεύτερον να έχουμε εξακριβώσει ότι οι στρατηγικές που θα ακολουθήσουμε έχουν πράγματι αποτέλεσμα και θα διευκολύνουν την επίτευξη του στόχου μας.
3. << Τα αυτό-αναπτυσσόμενα μοντέλα>>: Τα μοντέλα αυτά ακολουθούν ένα μοτίβο και αναπτύσσονται με τη συμμετοχή των ίδιων των παιδιών. Στη ρεαλιστική μάθηση υπάρχει μια συγκεκριμένη πορεία που μπορούμε ν’ ακολουθήσουμε. Αρχικά μεταφέρουμε το διατυπωμένο σε φυσική γλώσσα πρόβλημα στη συμβολική γλώσσα των μαθηματικών, ώστε να προχωρήσουμε στην ανάλυση και δόμηση του μαθηματικού προβλήματος και τέλος καταλήγουμε στην αναζήτηση της λύσης του προβλήματος.
Το υλικό που θα χρησιμοποιήσουμε αποτελείται από το λογισμικό kidspiration, ξυλάκια cuisenaire, πλαστικές μπάλες και φυσικά υλικά αντικείμενα. Για να μπορέσουμε να βοηθήσουμε τα παιδιά να κατανοήσουν τον πολλαπλασιασμό ως επαναλαμβανόμενη πρόσθεση μπορούμε να οργανώσουμε διάφορες δραστηριότητες μέσα στις οποίες θα δημιουργήσουμε τα πλαίσια για να χρησιμοποιήσουν τα παιδιά το εκπαιδευτικό υλικό.Για παράδειγμα μπορούμε αρχικά να μοιράσουμε στα παιδιά τα ξυλάκια cuisenaire και να τους εξηγήσουμε τον τρόπο με τον οποίο χρησιμοποιούνται δηλαδή ότι το μικρότερο απο τα ξυλάκια αντιστοιχεί σε μία μονάδα ενώ δέκα μονάδες που απαρτίζουν μία δεκάδα αντιστοιχούν στο μεγαλύτερο ξυλάκι.
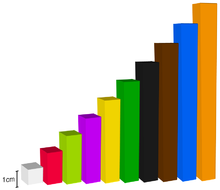
Έπειτα θα χρησιμοποιήσουμε τα ξυλάκια για να εισάγουμε τα παιδιά στην μαθηματική πράξη της πρόσθεσης. Κύριος στόχος είναι να συνειδητοποιήσουν τα παιδιά ότι η πρόσθεση είναι η πράξη που αφορά την ομαδοποίηση ομοειδών αντικειμένων-πραγμάτων,που οδηγεί σε ένα άθροισμα. Σε πρακτικό επίπεδο θα τοποθετήσουμε μπροστά στα παιδιά τα ξυλάκια cuisinaire, τα οποία θα έχουμε χωρίσει σε ισάριθμες ομάδες. Για παράδειγμα 4 ομάδες που αποτελούνται από 2 ξυλάκια. Θα ζητήσουμε από τα παιδιά να ανακατέψουν τα ξυλάκια και να τα μετρήσουν ένα ένα. Έπειτα θα τους ζητήσουμε να δημιουργήσουν 4 ομάδες που θα αποτελούνται από ισάριθμα ξυλάκια ώστε να συνειδητοποιήσουν σιγά σιγά ότι προσθέτοντας 2+2+2+2 οδηγεί στο αποτέλεσμα 8. Τέλος θα τους επισημάνουμε ότι σε αυτό το αποτέλεσμα μπορούμε να οδηγηθούμε και μέσω της πράξης του πολλαπλασιασμού που είναι 2*4.
Την ίδια διαδικασία μπορούμε να ακολουθήσουμε και με τα χρωματιστά μπαλάκια και τα φυσικά υλικά. Τοποθετούμε δηλαδή τα υλικά σε ομάδες ίσου αριθμού μπροστά στα παιδιά και μέσω πειραματισμών τα βοηθάμε να καταλήξουν στο συμπέρασμα που θέλουμε.
Τέλος, πολύ χρήσιμο παιδαγωγικό υλικό kidspiration καθώς περιέχει πλούσιο υλικό ασκήσεων και εφαρμογών για την καλύτερη κατανόηση του πολλαπλασιασμού.


Αφόρμηση: Παλιά συνταγή για φρουτοσαλάτα που βρήκα στο μπαούλο της γιαγιάς.
Υλικά δραστηριότητας: 9 μήλα, 6 πορτοκάλια,3 αχλάδια,πλαστικό μαχαιράκι,πιάτα.

Μέθοδοι Διδασκαλίας: Ερωτήσεις- Απαντήσεις, Διάλογος, Εισήγηση,Παιχνίδι.
Στόχοι:
1. Να προσθέτουν διαδοχικά τους αριθμούς από τα υλικά που χρειάζονται για την φρουτοσαλάτα. (Παιδί και Μαθηματικά)
2. Να εξοικειωθούν με το πρόγραμμα kidspiration. (Παιδί και Πληροφορική)
3. Να διηγηθούν τα βήματα της συνταγής χρησιμοποιώντας διατακτικά αριθμητικά επίθετα.(Παιδί και Γλώσσα- Προφορικός Λόγος)
Σκοπός: Να διευρύνουν τις γνώσεις τους για τον πολλαπλασιασμό χρησιμοποιώντας μαθηματικούς όρους.
Χρόνος: 45 λεπτά
Πορεία διδασκαλίας:
Αρχικά δημιουργούμε στα παιδια ένα νοητικό υπόβαθρο λέγοντας τους ότι χτες που καθαρίζαμε τη σοφίτα του σπιτιού βρήκαμε ένα μπαούλο που μέσα περιείχε χαρτιά με σπιτικές συνταγές που έφτιαχνε η γιαγιά μας. Έτσι αποφασίσαμε να φέρουμε στην τάξη μια συνταγή που μας άρεσε και την περάσαμε στον ηλεκτρονικό υπολογιστή.
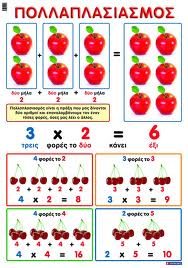
Στη συνέχεια τους λέμε ότι είναι σημαντικό να τρώμε φρούτα γι’ αυτό θα ήταν καλό να φτιάξουμε 3 φρουτοσαλάτες για να φάνε όλα τα παιδιά της τάξης. Έτσι τα οδηγούμε στις μαθηματικές πράξεις του πολλαπλασιασμού. Τα βοηθάμε να οδηγηθούν στο συμπέρασμα ότι 3+3+3 μας κάνουν 9 μήλα, όσα δηλαδή θα χρειαστούμε για να φτιάξουμε 3 φρουτοσαλάτες και τέλος ότι δε χρειάζεται να μετράμε κάθε φορά τα μήλα αλλά να εφαρμόζουμε τον πολλαπλασιασμό, δηλαδή 3*3=9. Το ίδιο συμβαίνει και με τις μαθηματικές πράξεις 2+2+2=6 που είναι τα πορτοκάλια της συνταγής,η οποία αντιστοιχεί στην πράξη 2*3=6 αλλά και με τα αχλάδια τα οποία είναι 1+1+1=3, άρα με βάση τον πολλαπλασιασμό 1*3.
Αφού βρουν τις απαντήσεις στον υπολογιστή, προχωράμε στην εκτέλεση της συνταγής ζητώντας από τα παιδιά να κόψουν τα φρούτα και να χρησιμοποιήσουν διατακτικά αριθμητικά επίθετα(πρώτο βήμα, δεύτερο βήμα κτλ) για να περιγράψουν σταδιακά τη διαδικασία που θα ακολουθήσουν.
Τέλος σαν αξιολόγηση τους δίνουμε ένα φυλλάδιο εργασίας πάνω στο οποίο υπάρχουν ασκήσεις πολλαπλασιασμού με συμπλήρωση των κενών.
Ζαχάρος, Κ. (2007). Οι μαθηματικές έννοιες στην προσχολική εκπαίδευση και η διδασκαλία τους. Επιστήμες της Αγωγής · Διδακτική - Αναλυτικά Προγράμματα - Αξιολόγηση. Β. Βασιλού - Παπαγεωργίου (Επιμελ. Σειράς). Αθήνα : Μεταίχμιο
Τζεκάκη, Μ. (2007) Μικρά παιδιά, μεγάλα μαθηματικά νοήματα : Προσχολική και πρώτη σχολική ηλικία. Παιδαγωγική Σειρά. Αθήνα : Gutenberg - Γιώργος & Κώστας Δαρδανός
http://math.cilenia.com/el http://users.sch.gr/ndelis/thales/ver1/askpro.html